
第五讲反函数 主讲人:卢自娟
函数、极限与连续 第五讲 反函数 主讲人:卢自娟
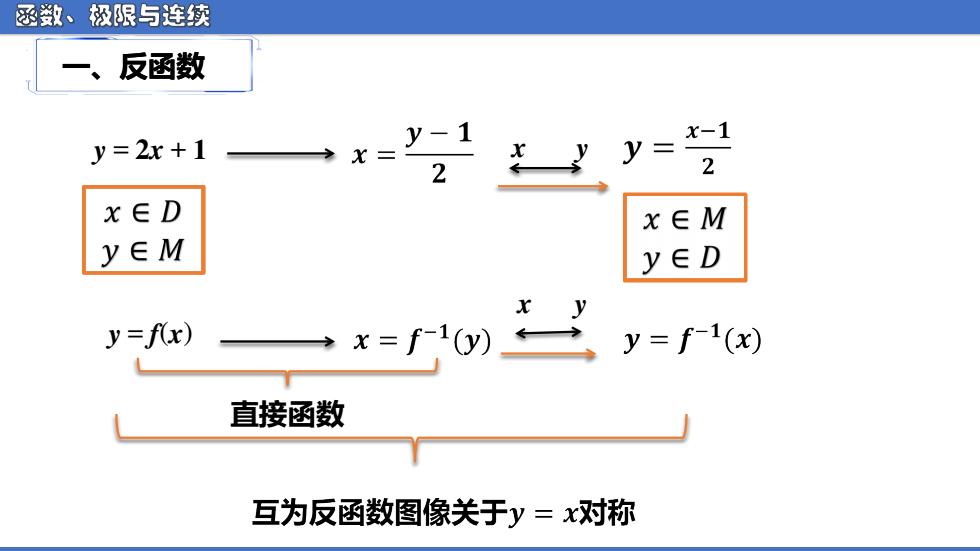
逐数、极限与连续 一、反函数 y=2r+1 →x= y-1 y= -1 2 2 x∈D x∈M y∈M y∈D y=f(x) 直接函数 互为反函数图像关于y=x对称
函数、极限与连续 ᵉ = ᵽ ᵉ + ᵼ ᵉ ᵉ ᵉ = ᵈ(ᵉ ) ᵉ ᵉ 直接函数 一、反函数

还数、极限与连续 一、反函数 定义1:函数f(x)的定义域为D,值域为M,若对于 每一个yEM,都有唯一的x∈D适合y=f(x),从而 定义了M上的新函数,这个新函数称为y=f(x) 的反函数。 记作:x=f-1(y) 习惯 =f八{
函数、极限与连续 定义1: 习惯 ᵆ ∈ ᵄ ᵆ ∈ ᵃ 一、反函数

函数、极限与连续 例1:求下列函数的反函数: 2X+3 (1) y=2x+1 (2) y= x+2 解: x=y-1 解:yx+2)=2x+3 2 x与y x(y-2)=-2y+3 互换 3-2y x-1 X二 y= y-2 2 3-2x y= x卡2 X-2 互为反函数图像关于y=x对称
函数、极限与连续 求下列函数的反函数: (1) ᵉ = ᵽ ᵉ + ᵼ 解: 例1: (2) 解: ᵉ (ᵉ + ᵽ ) = ᵽ ᵉ + ᵽ ᵉ (ᵉ − ᵽ ) = − ᵽ ᵉ + ᵽ ᵉ ≠ ᵽ

丞数、极限与连续 (3) y=2r+1 解: 2x=y-1 lg 22"lgg 2(y-1) x=lg 2(y-1) y=lgg 2(x-1) x>1
函数、极限与连续 (3) ᵉ = ᵽ ᵉ + ᵼ 解: ᵽ ᵉ = ᵉ − ᵼ ᵈᵉᵈ ᵽ ᵽ ᵉ = ᵈᵉᵈ ᵽ (ᵉ − ᵼ ) ᵉ = ᵈᵉᵈ ᵽ (ᵉ − ᵼ ) ᵉ = ᵈᵉᵈ ᵽ (ᵉ − ᵼ ) ᵉ > ᵼ