
第四讲 无穷小
函数极限与连续 第四讲 无穷小
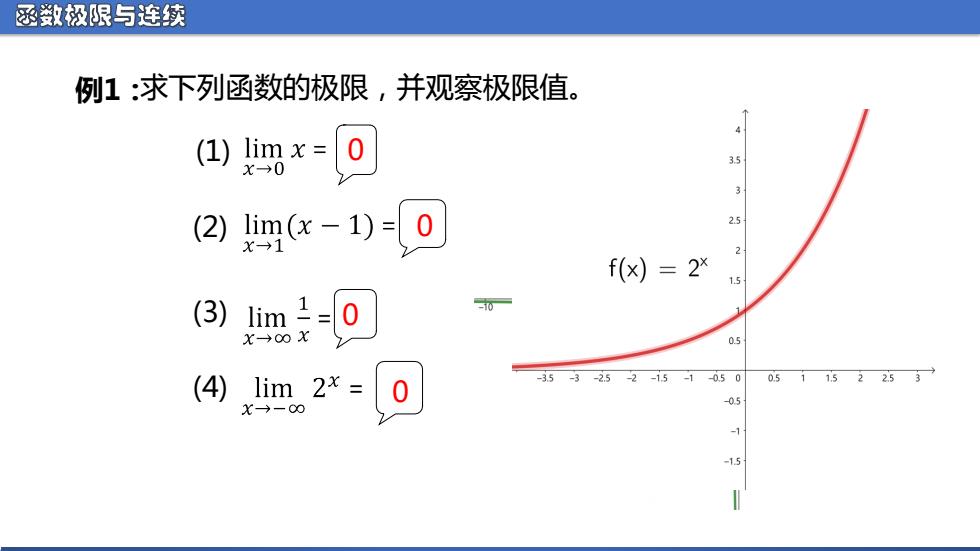
函数极限与连续 例1:求下列函数的极限,并观察极限值。 (1)lim x X→0 0 3 (2) mx-1)-0 25 fx)=2 3)m0 0 X→00X (4)lim 2x= 35-3-25-2-15-10.50 0511522531 X→一00 0 -05 -15
函数极限与连续 例1:求下列函数的极限,并观察极限值。 (1) (2) (3) 0 0 0 (4) 0

函叙极限与连续 1.无穷小量 定义1: 极限为0的变量,称为无穷小量,简称无穷小。 记:lima(x)=0,limB(x)=0 X→X0 limx=2 lim= X→2 X→3X 3 说 (1)说函数是无穷小,须指明自变量的变化趋势; 明 (2)0是唯一可作为无穷小的常数,绝对值很小 的非零常数不是无穷小;
函数极限与连续 定义1: 记: 极限为0的变量,称为无穷小量,简称无穷小。 说 明: (1) 说函数是无穷小,须指明自变量的 变化趋势; (2) 0是唯一可作为无穷小的常数,绝对值很小 的非零常数不是无穷小; 1 3 1.无穷小量 2

函数极限与连续 1.无穷小量的性质 (1)有限个无穷小的代数和为无穷小; 说明:离开了有限,结论不一定成立。 反例:lim n-→+0 +后+是 ( +.+是) lim 1+2+3+.+m n→+o∞ n2 lim n+=lim n2+n 2n2 n-→+o2n2 =m+分)=月
函数极限与连续 (1)有限个无穷小的代数和为无穷小; 说明: 离开了有限,结论不一定成立。 反例: 1.无穷小量的性质

函微极限与连续 (2)有限个无穷小的乘积为无穷小; 如 lim(x·simx)=0 x→0 但 无限个无穷小的乘积为无穷小;X (3)常数与无穷小的乘积为无穷小
函数极限与连续 (2)有限个无穷小的乘积为无穷小; (3)常数与无穷小的乘积为无穷小。 如 但 无限个无穷小的乘积为无穷小; ×