
绪论 微积分发展史概述 主讲人:卢自娟
绪论 微积分发展史概述 主讲人:卢自娟

微积分学就是微分学和 积分学的总称。 《天限细分”就是微分; 《无限求和”就是积分
微积分学就是微分学和 积分学的总称。 “无限求和” 就是微分; 就是积分。 “无限细分
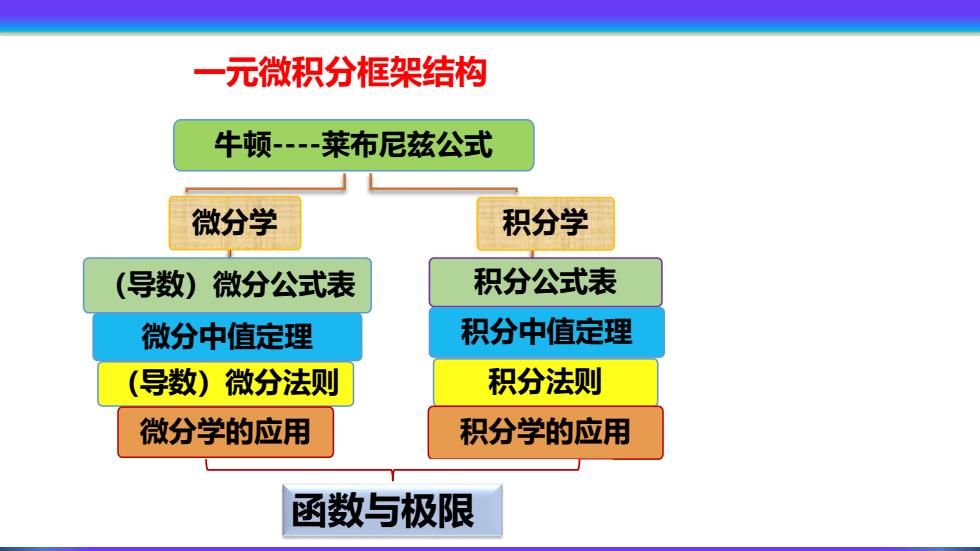
一元微积分框架结构 牛顿-莱布尼兹公式 微分学 积分学 (导数) 微分公式表 积分公式表 微分中值定理 积分中值定理 (导数)微分法则 积分法则 微分学的应用 积分学的应用 函数与极限
一元微积分框架结构 牛顿-莱布尼兹公式 微分学 (导数)微分公式表 微分中值定理 (导数)微分法则 微分学的应用 积分学 积分公式表 积分中值定理 积分法则 积分学的应用 函数与极限

牛顿 英国人 数学家物理学家天文学家 巴罗:指导教师 物理问题作为研究背景 函数增量与自变量增量 △S ds 之比 △t 'dt 求变化率与求面积是两个互逆问题
牛顿 英国人 物理学家 天文学家 巴罗: 指导教师 物理问题作为研究背景 函数增量与自变量增量 之比 求变化率与求面积是两个互逆问题. 数学家 ∆𝒔 ∆𝒕 → 𝒅𝒔 𝒅𝒕

莱布尼兹 德国数学家、哲学家 巴罗 《几何讲义》 几何问题出发: 函数增量与自变量增量 的依赖关系-.微分 △y=A△x+O(△x) 微分与积分是互逆关系
莱布尼兹 德国数学家、哲学家 巴罗- 《几何讲义》 几何问题出发: 函数增量与自变量增量 的依赖关系- 微分 微分与积分是互逆关系。 ∆𝒚 = 𝑨∆𝒙 +o(∆𝒙)