
第一讲 数列的极限(n→∞)
上页 下页 首页 第一讲 数列的极限(n→∞)

函数、极限与连续 2、几种特殊的数列极限 3、数列极限的运算法则
函数、极限与连续 1、数列极限的定义 2、几种特殊的数列极限 3、数列极限的运算法则 一、数列的极限

函数、极限与连续 刘徽的割圆术: 割之弥细,所失弥少,割之又割,则与圆合体而无所失矣
函数、极限与连续 刘徽的割圆术: 割之弥细,所失弥少,割之又割,则与圆合体而无所失矣
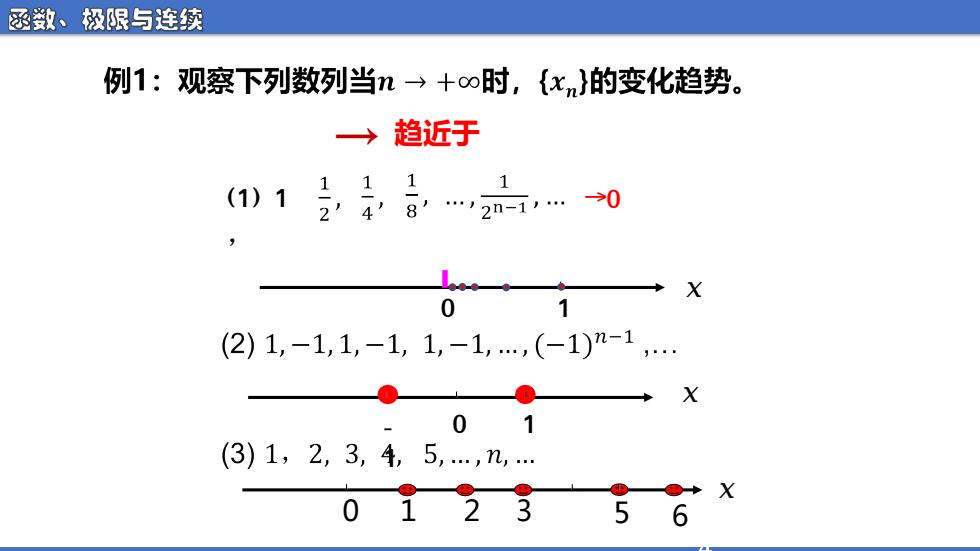
函数、极限与连续 例1:观察下列数列当n→+o时,{xn}的变化趋势。 趋近于 (1)13,4,8,2n-.→0 0 1 (2)1,-1,1,-1,1,-1,(-1)n-1, X 01 (3)1,2,3,4,5,. 01235 @X 6
函数、极限与连续 (1) 1 , ᵆ 0 1 ᵆ 1 →0 - 1 0 ᵆ 0 1 2 3 5 6 4 → 趋近于
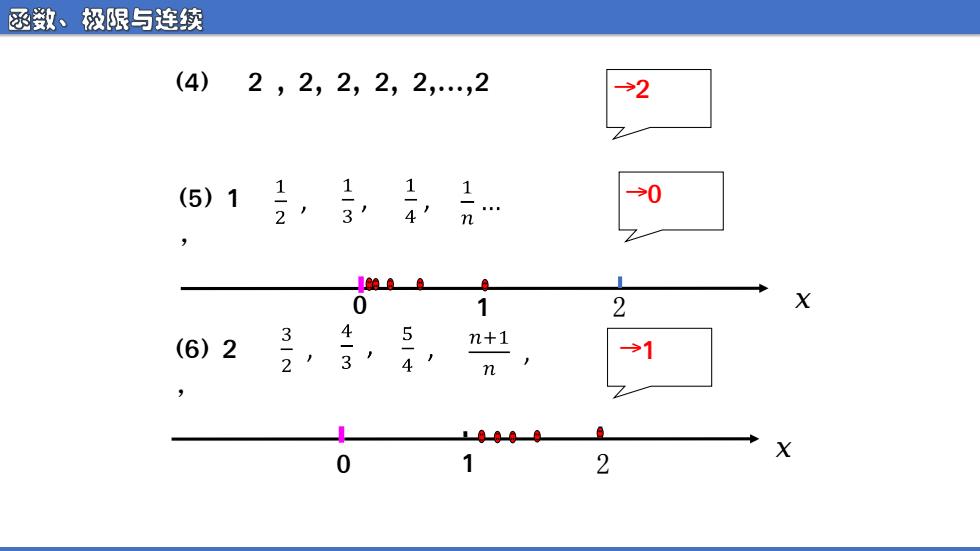
函数、极限与连续 (4) 2,2,2,2,2,.,2 →2 (5)1 2, 1 1 3,4 →0 n. 0 1 2 3 4 5 (6)2 n+1 1 2’ 3 4 2 X 0
函数、极限与连续 (4) 2 , 2, 2, 2, 2,.,2 (6) 2 , (5) 1 , →2 →0 →1 0 1 2 ᵆ 0 1 2 ᵆ