
第五讲 无穷大与无穷小
函数极限与连续 第五讲 无穷大与无穷小
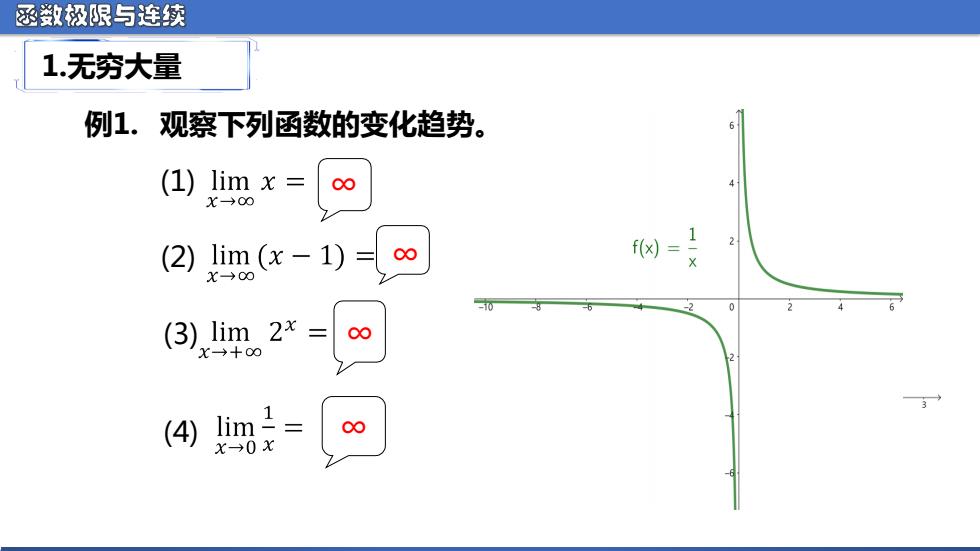
函极限与连续 1.无穷大量 例1.观察下列函数的变化趋势。 (1) limx= X→00 1 (2)1 im(x-1)=∞ f(x)= X→00 -0 (3)lim 2x 00 X→+00 (4 lim= 00 X→0X
函数极限与连续 例1. 观察下列函数的变化趋势。 (1) (2) (3) ∞ ∞ ∞ (4) ∞ 1.无穷大量

函数极限与连续 1.无穷大量 定义1 若当x一x0(或x一→o∞)时,函数f(x)的 绝对值无限增大则称f(x)是x→x(或x→∞)的 无穷大量,简称无穷大。 说明:(1)说函数是无穷大,须指明自变量的变化趋势; (2)绝对值很大的常数不是无穷大; (3)“∞”只是一种记法,此时函数的极限 不存在
函数极限与连续 定义1 : 说明: (1) 说函数是无穷大,须指明自变量的 变化趋势; (3) “∞ ”只是一种记法,此时函数的极限 不存在。 (2) 绝对值很大的常数不是无穷大; 1.无穷大量
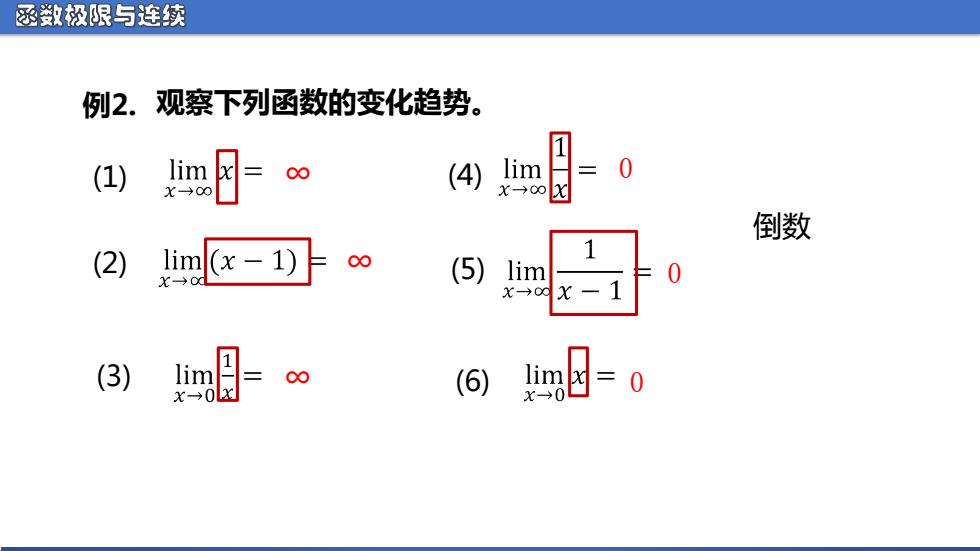
函叙极限与连续 例2.观察下列函数的变化趋势。 (1) (4) lim =0 X→00 倒数 (2) [x-1)∞ (5)1im 0 X→00 (3) 目。日-0
函数极限与连续 (1) (2) (3) ∞ (4) (5) (6) 0 ∞ ∞ 0 0 例2. 观察下列函数的变化趋势。 倒数

函数极限与连续 2无穷大与无穷小的关系 定理2在自变量的同一变化过程中, 如果f(田为无穷大,则是无穷小 如果f(x)为无穷小,且f(x)≠0, 则 是无穷大
函数极限与连续 定理2 : 在自变量的同一变化过程中, 2.无穷大与无穷小的关系