
关于定义的几点说明 (1)EX)是一个实数,而非变量,它是一种加 权平均,与一般的平均值不同,它从本质上体现 了随机变量X取可能值的真正的平均值,也称 均值. (2)级数的绝对收敛性保证了级数的和不 随级数各项次序的改变而改变,之所以这样要 求是因为数学期望是反映随机变量X取可能值 的平均值,它不应随可能值的排列次序而改变. (3)随机变量的数学期望与一般变量的算 术平均值不同
关于定义的几点说明 (3) 随机变量的数学期望与一般变量的算 术平均值不同. (1) E(X)是一个实数,而非变量,它是一种加 权平均,与一般的平均值不同 , 它从本质上体现 了随机变量 X 取可能值的真正的平均值, 也称 均值. (2) 级数的绝对收敛性保证了级数的和不 随级数各项次序的改变而改变 , 之所以这样要 求是因为数学期望是反映随机变量X 取可能值 的平均值,它不应随可能值的排列次序而改变

X 2 假设 0.02 0.98 随机变量X的算术平均值为 1+ 2=1.5, 2 E(X)=1×0.02+2×0.98=1.98. 它从本质上体现了随机变量X取可能值的平均值 当随机变量X取各个可能值是等概率分布时,X 的期望值与算术平均值相等
x O • 随机变量 X 的算术平均值为 1.5, 2 1 2 = + 假设 E(X) = 1 0.02 + 2 0.98= 1.98. 它从本质上体现了随机变量X 取可能值的平均值. 当随机变量 X 取各个可能值是等概率分布时 , X 的期望值与算术平均值相等. • 1 • 2 • • X 1 2 p 0.02 0.98
实例1谁的技术比较好? 甲、乙两个射手,他们射击的分布律分别内 击中环数 8 10 甲射手 概率 0.30.10.6 击中环数 8 9 10 乙射手 概率 0.20.50.3 试问哪个射手技术较好?
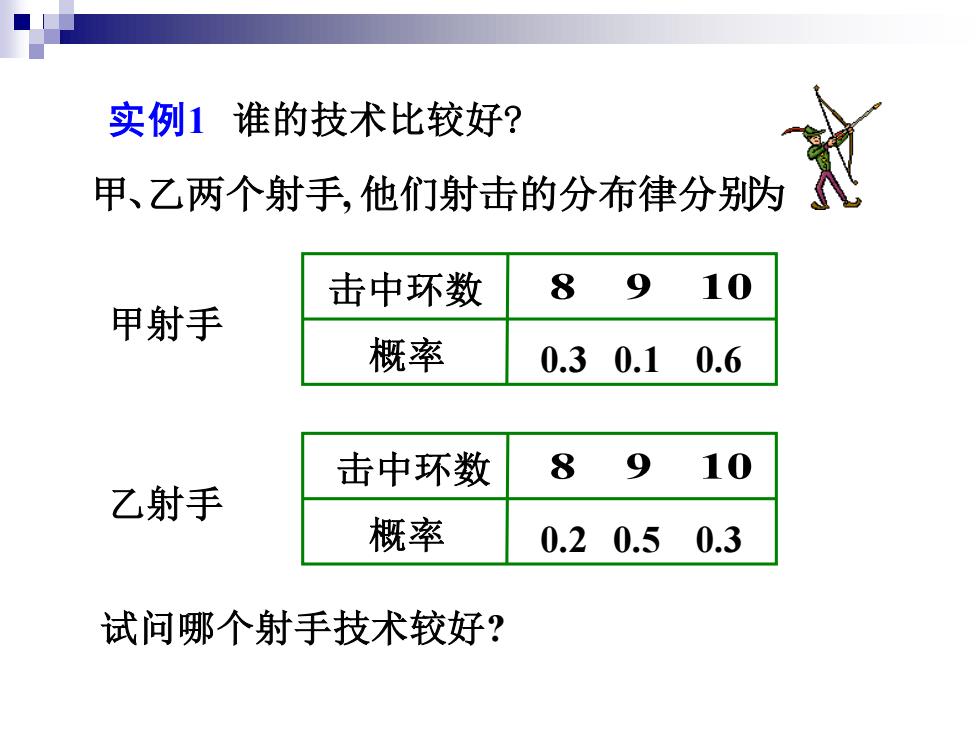
甲、乙两个射手, 他们射击的分布律分别为 试问哪个射手技术较好? 实例1 谁的技术比较好? 乙射手 击中环数 概率 8 9 10 0.2 0.5 0.3 甲射手 击中环数 概率 8 9 10 0.3 0.1 0.6

解设甲、乙射手击中的环数分别为X,X2· E(X1)=8×0.3+9×0.1+10×0.6=9.3(环), E(X2)=8×0.2+9×0.5+10×0.3=9.1(环), 故甲射手的技术比较好
解 ( ) 8 0.3 9 0.1 10 0.6 9.3( ), E X1 = + + = 环 ( ) 8 0.2 9 0.5 10 0.3 9.1( ), E X2 = + + = 环 , . 设甲、乙射手击中的环数分别为 X1 X2 故甲射手的技术比较好

实例2发行彩票的创收利润 某一彩票中心发行彩票10万张,每张2元.设 头等奖1个,奖金1万元,二等奖2个,奖金各5千元; 三等奖10个,奖金各1千元;四等奖100个,奖金各 100元;五等奖1000个,奖金各10元.每张彩票的成 本费为0.3元,请计算彩票发行单位的创收利润. 解设每张彩票中奖的数额为随机变量X,则 X10000 5000 1000 100 10 0 p 1/105 2/10s 10/105100/1051000/10P0
实例2 发行彩票的创收利润 某一彩票中心发行彩票 10万张, 每张2元. 设 头等奖1个, 奖金 1万元, 二等奖2个,奖金各 5 千元; 三等奖 10个, 奖金各1千元; 四等奖100个, 奖金各 100元; 五等奖1000个, 奖金各10 元.每张彩票的成 本费为 0.3 元, 请计算彩票发行单位的创收利润. 解 设每张彩票中奖的数额为随机变量X, 则 X p 10000 5000 1000 100 10 0 5 1 10 5 2 10 5 10 10 5 100 10 5 1000 10 p0