
11-1 静力法做单跨梁的影响线 影响线基本规律 剪力影响线在截面两侧平行,数值差值为1,截面处有突变 ●弯矩影响线在截面处有折点; 伸臂梁影响线(与简支梁比较) ●支反力影响线:只需将简支梁反力影响线在伸臂部分延伸; ●内力影响线:截面在简支梁部分时,其影响线是将简支梁截 面影响线延长到伸臂部分; ●内力影响线:截面在伸臂部分时,其影响线与悬臂梁相同;
⚫ 剪力影响线在截面两侧平行,数值差值为1,截面处有突变 影响线基本规律 伸臂梁影响线(与简支梁比较) ⚫ 弯矩影响线在截面处有折点; 11-1 静力法做单跨梁的影响线 ⚫ 支反力影响线:只需将简支梁反力影响线在伸臂部分延伸; ⚫ 内力影响线:截面在简支梁部分时,其影响线是将简支梁截 面影响线延长到伸臂部分; ⚫ 内力影响线:截面在伸臂部分时,其影响线与悬臂梁相同;
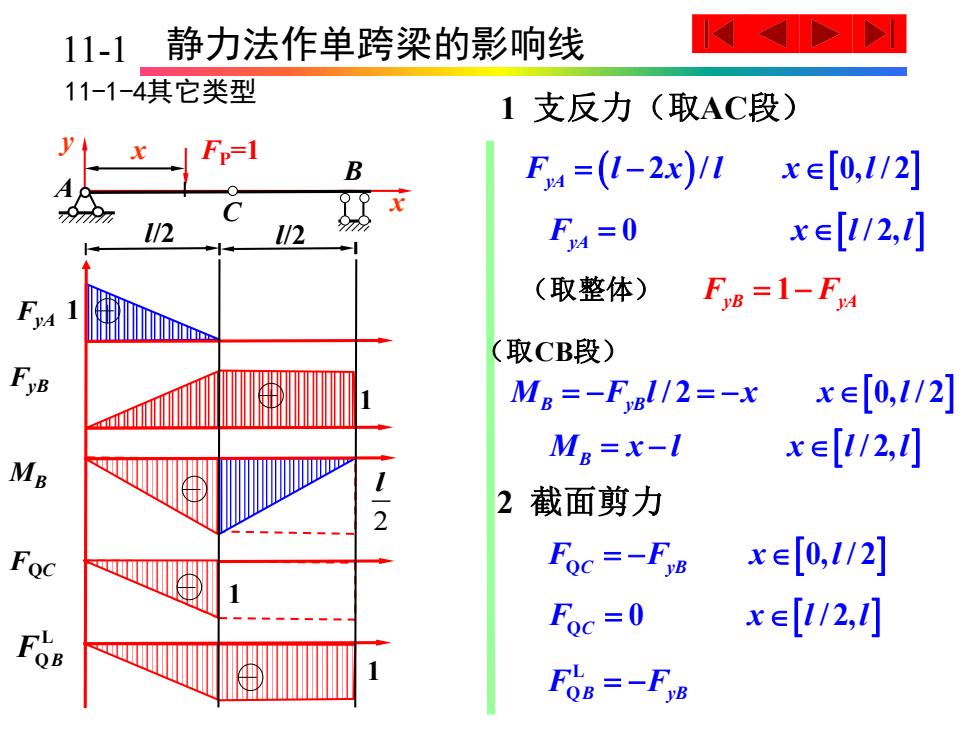
11-1 静力法作单跨梁的影响线 11-1-4其它类型 1支反力(取AC段) p=1 B F4=(l-2x)/lx∈[0,l/2] 99 L2 L/2 F,4=0 x∈[/2,] (取整体) Fy8=1-FA (取CB段) FyB Mg=-Fgl/2=-x x∈[0,l/2] Mp=x-I ID x∈[/2,] 2截面剪力 Foc Foc=-F)B xe[0,l/2] Foc=0 x∈[/2,] FoB=-FyB
5-1 静力法作单跨梁的影响线 11-1-4其它类型 FyA 1 1 支反力(取AC段) F l x l x l yA = − ( 2 / 0, / 2 ) FyB 1 x FP=1 A B y x l/2 C l/2 F x l l yA = 0 / 2, 1 F F yB yA = − M x l x l l B = − / 2, M F l x x l B yB = − = − / 2 0, / 2 2 MB l 2 截面剪力 F x l l QC = 0 / 2, 1 FQC F F x l QC yB = − 0, / 2 L F F QB yB = − L FQB 1 11-1 (取整体) (取CB段)
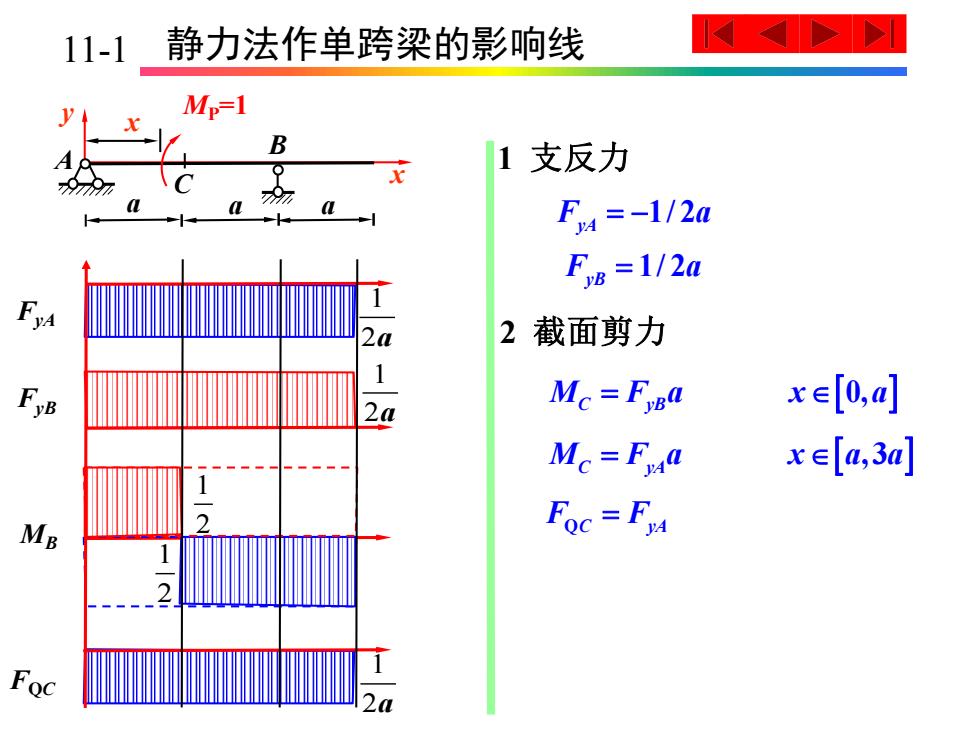
11-1 静力法作单跨梁的影响线 ✉> Mp=1 B 1 支反力 99z F4=-l/2a F,B=1/2a 2 截面剪力 FyB 2a Mc=Fypa xe[o,a个 Mc=Fya xe[a,3a] MB Foc=Fy Foc 2a
5-1 静力法作单跨梁的影响线 1 2a 1 2a 1 2a 1 2 1 2 FyA 1 支反力 1/ 2 F a yA = − FyB M F a x a a C yA = , 3 MB 2 截面剪力 FQC F F QC yA = a x MP=1 A B y x a C a 1/ 2 F a yB = M F a x a C yB = 0, 11-1

静力法作静定列架影响线 求Fc,ME,FNE,M,FoD影响线 1.Fgc,影响线 B x<l/4 Foc=-1 M. 414 1/2 x>l/4 Foc =0 Q影响线 x-l12 2.ME,FvE影响线 N影响线 O ME(右拉为正) FE=-1 2 M影响线 /2 ME=-(x-l/2) (0≤x≤)
静力法作静定刚架影响线 1 FNE = − 求 FQC , ME , FNE , MD , FQD影响线 x l / 4 M (x l / 2) E = − − 1 FQC = − QC影响线 1 C D l/4 l/2 A B 1 l/4 E x 1. FQC , 影响线 x l / 4 0 FQC = 2. ME , FNE影响线 FNE1 ( ME 右拉为正) x − l / 2 NE影响线 1 ME影响线 l/2 l/2 (0 ) x l FQC 1 Mc FQC Mc
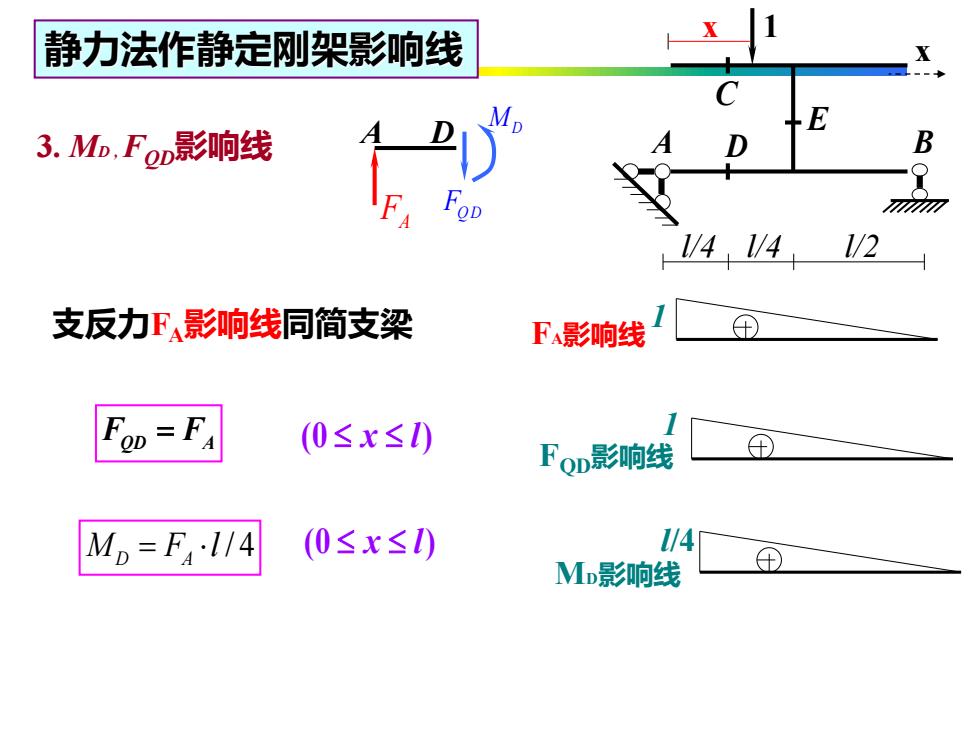
静力法作静定刚架影响线 3.M,FoD影响线 B 支反力影响线同简支梁 F影响线 FOD=FA (0≤x≤I) FoD影响线 M=FA·l/4 (0≤x≤) 14 MD影响线
静力法作静定刚架影响线 3. MD ,FQD影响线 F F QD A = C D l/4 l/2 A B 1 l/4 E x x / 4 M F l D A = 1 FA影响线 MD影响线 l/4 MD FA FQD A D (0 ) x l 1 FQD影响线 支反力FA影响线同简支梁 (0 ) x l