上海交通大学：《概率论与数理统计》课程教学资源（课件讲义）第六章 数理统计的基本概念 6.2 抽样分布

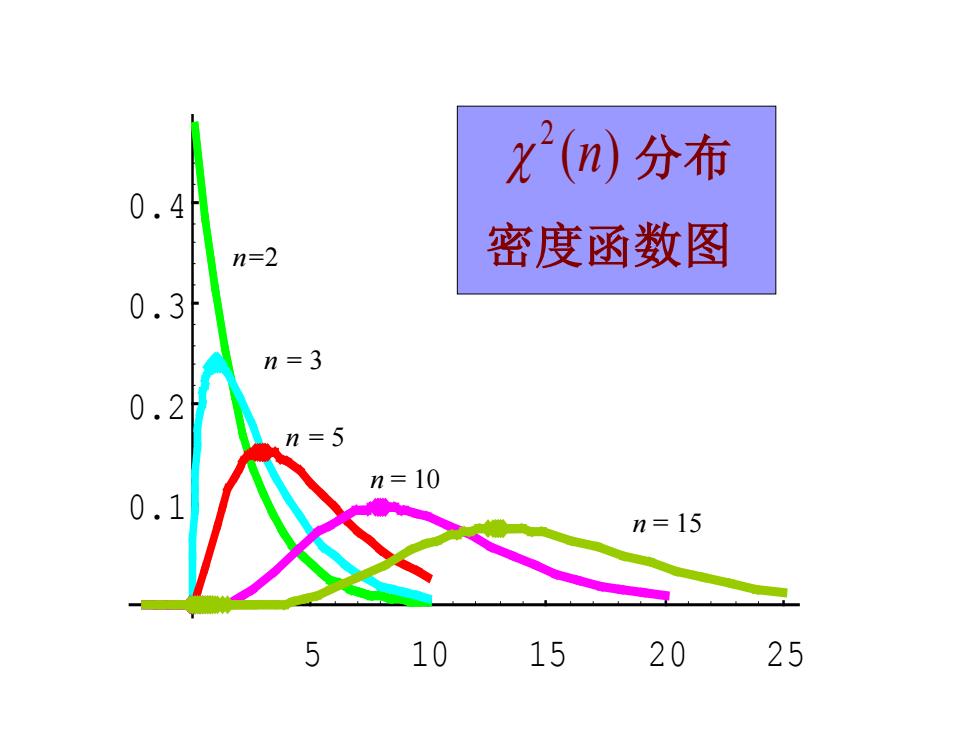
t2(n)分布 0.4 n=2 密度函数图 0.3 n=3 0.2 n=5 n=10 0. n=15 10 15 20 25

5 10 15 20 25 0.1 0.2 0.3 0.4 n=2 n = 3 n = 5 n = 10 n = 15 分布 密度函数图 ( ) 2 χ n

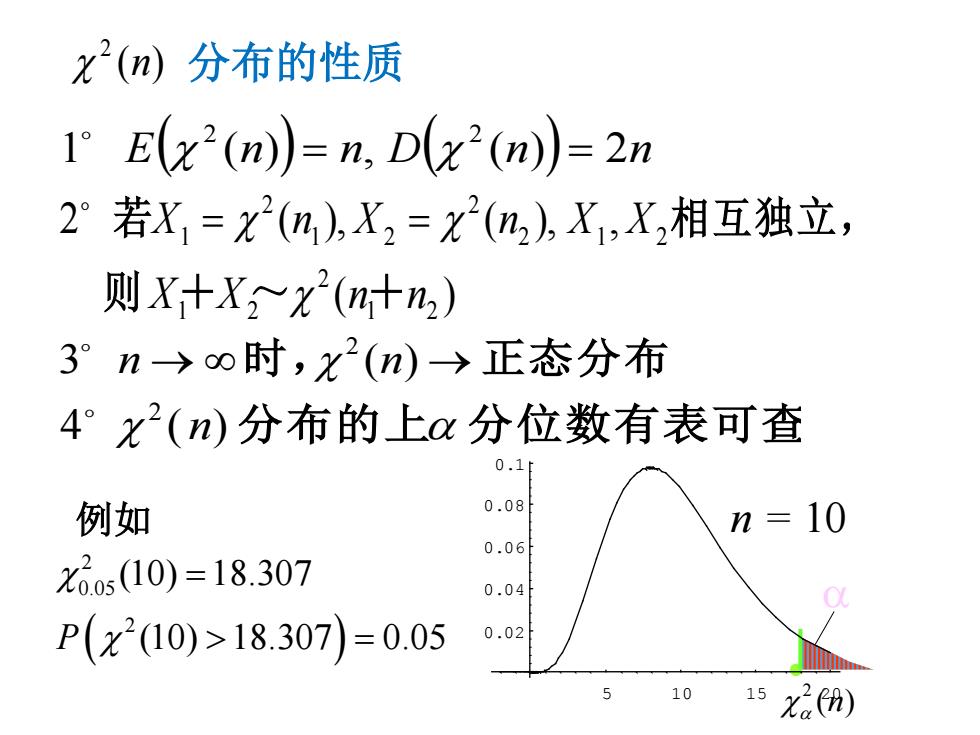
x(n)分布的性质 I E(x2(n))=n,D(x"(n))=2n 2°若X1=x2(n),X2=X2(n),X1,X相互独立， 则X+X>x2(n十n) 3°n→o时，x2(n)→正态分布 4°x2(n)分布的上分位数有表可查 0.1 例如 0.08 n=10 0.06 X6s(10)=18.307 0.04 P(x2(10)>18.307=0.05 0.02 10 15X2m)

1 E( (n)) n, D( (n)) 2n 2 2 χ = χ =  α ( ) 2 ( ), ( ), , 1 2 2 1 2 2 1 2 2 1 2 2 1 X X n n X n X n X X 则 ＋ ～ ＋ 若 相互独立， χ = χ = χ  3 n → ∞时，χ2 (n) → 正态分布 4 χ2 ( n) 分布的上α 分位数有表可查 ( ) 分布的性质 2 χ n • 例如 ( ) 2 0.05 2 (10) 18.307 P (10) 18.307 0.05 χ χ = > = 5 10 15 20 0.02 0.04 0.06 0.08 0.1 n = 10 2 ( ) n χα

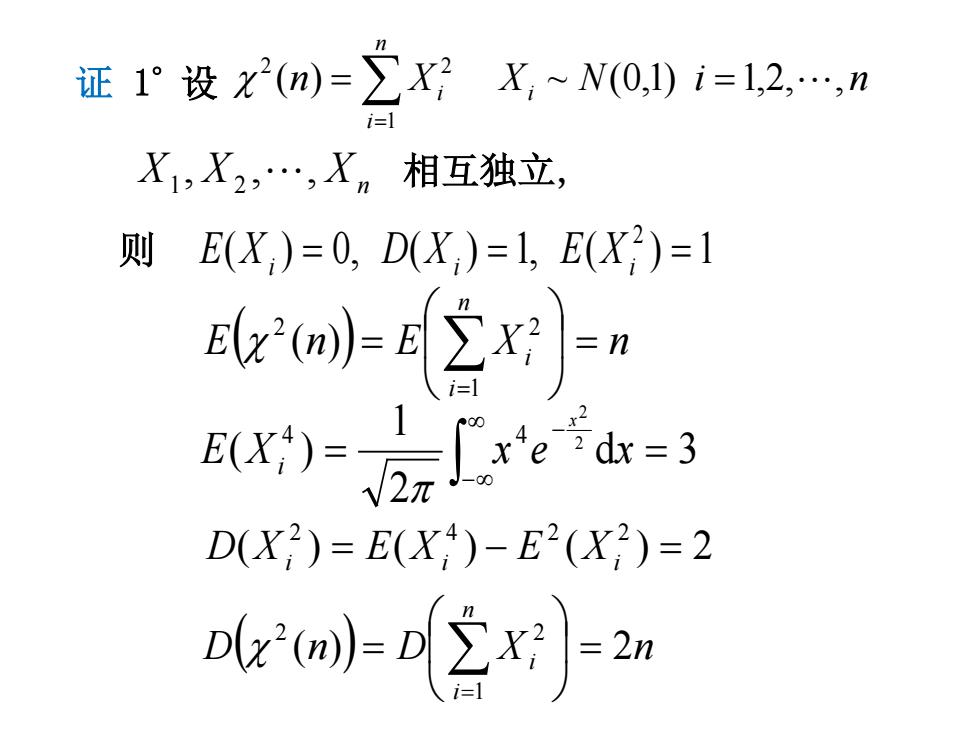
证1°设x2()）=∑X好X,N(0,)i=1,2,…,n i1 X1,X2,…,X,n相互独立， E(X)=0,D(X)=1,E(X)=1 则 -42x好=n D(X)=E(X4)-E2(X2)=2 ()2n

X X Xn , , , 1 2  相互独立, 证 1° 设 ∑= = = n i i i n X X N i n 1 2 2 χ ( ) ~ (0,1) 1,2,, 则 ( ) 0, ( ) 1, ( ) 1 2 = = = E Xi D Xi E Xi E( n ) E X n n i i  =      = ∑=1 2 2 χ ( ) d 3 2 1 ( ) 2 2 4 4 = = ∫ ∞ −∞ − E X x e x x i π ( ) ( ) ( ) 2 2 4 2 2 D Xi = E Xi − E Xi = D( n ) D X n n i i ( ) 2 1 2 2  =      = ∑= χ

t分布 定义设X~N(0,1),Y~x(n),X,Y相互独立， T 则T所服从的分布称为自由度为n的t分布其密 度函数为 f(t)= r2 1 -0<t<0 nx r n

t 分布 定义 则T 所服从的分布称为自由度为 n 的t 分布其密 度函数为 n Y X T = − ∞ < < ∞         +             + = + − t n t n n n f t n 2 1 2 1 2 2 1 ( ) Γ Γ π ~ (0,1) , ~ ( ), 2 设X N Y χ n X , Y 相互独立

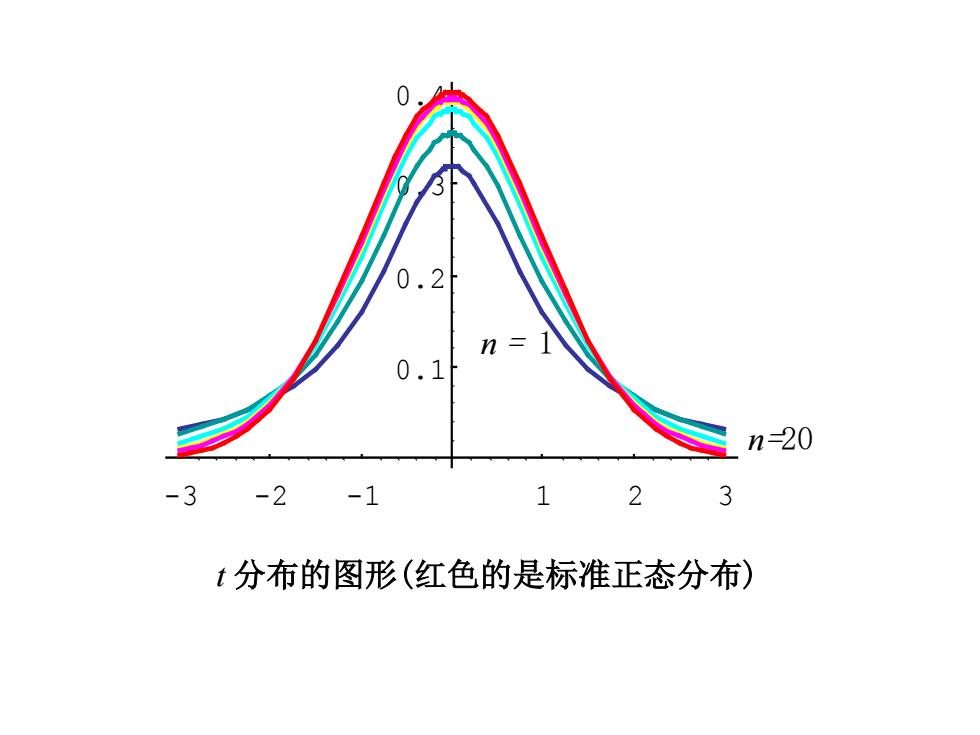
0.2 0.1 n20 -3 -2 -1 2 3 t分布的图形（红色的是标准正态分布）

t 分布的图形(红色的是标准正态分布) n = 1 n=20 -3 -2 -1 1 2 3 0.1 0.2 0.3 0.4