
导航 典型例题1】已知a=(2,-3,5),b=(-3,1,-4) (1)若c=(m,2,m),且ac,求c; (2)若p=(1x,y),且a⊥p,b⊥P,求p 解:(1).allc,∴.c=a, 即(m,2,n)=(2,-3,5), 2 m=2λ, =- ∴.2=-31,解得 m 3 -(2,9) n=51, m 三 3
导航 【典型例题1】已知a=(2,-3,5),b=(-3,1,-4). (1)若c=(m,2,n),且a∥c,求c; (2)若p=(1,x,y),且a⊥p,b⊥p,求p. 解:(1)∵a∥c,∴c=λa, 即(m,2,n)=λ(2,-3,5), ∴ 𝑚 = 2𝜆, 2 = -3𝜆, 𝑛 = 5𝜆, 解得 𝜆 = - 2 3 , 𝑚 = - 4 3 , 𝑛 = - 10 3 . ∴c= - 4 3 ,2,- 10 3

导航、 (2).'aLp,b⊥p, .ap=0,bp=0, 0 x=1, y=-1. ∴.p=(1,-1,-1)
导航 (2)∵a⊥p,b⊥p, ∴a·p=0,b·p=0, ∴ 2-3𝑥 + 5𝑦 = 0, -3 + 𝑥-4𝑦 = 0, 解得 𝑥 = -1, 𝑦 = -1. ∴p=(1,-1,-1)

导 专题二空间向量与空间中线、面的位置关系 设两条不同的直线l,m的方向向量分别为a,b,两个不同的平面 a,B的法向量分别为u,y,直线l¢平面α,则 (1)线线平行:lIlm台→aIlb台a=kb,k∈R; (2)线面平行:lIlo台a⊥u台au=0; (3)面面平行:aIB←台→uIv台u=kw,k∈R, (4)线线垂直:lLm→a⊥b台ab=0; (5)线面垂直:l⊥a台alu台a=ku,k∈R; (6)面面垂直:0⊥台u⊥v台→uv=0
导航 专题二空间向量与空间中线、面的位置关系 设两条不同的直线l,m的方向向量分别为a,b,两个不同的平面 α,β的法向量分别为u,v,直线l⊄平面α,则 (1)线线平行:l∥m⇔a∥b⇔a=kb,k∈R; (2)线面平行:l∥α⇔a⊥u⇔a·u=0; (3)面面平行:α∥β⇔u∥v⇔u=kv,k∈R; (4)线线垂直:l⊥m⇔a⊥b⇔a·b=0; (5)线面垂直:l⊥α⇔a∥u⇔a=ku,k∈R; (6)面面垂直:α⊥β⇔u⊥v⇔u·v=0
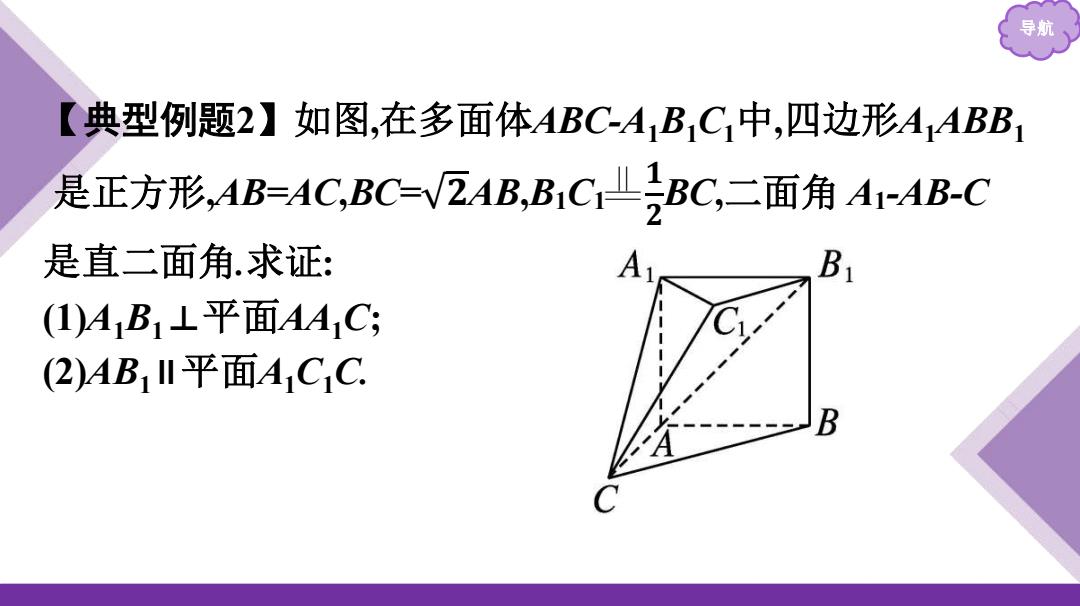
导 【典型例题2】如图,在多面体ABCA1B1C1中,四边形AABB1 是正方形,AB=AC,BC=V2AB,B1C1LBC,二面角AI-AB-C 是直二面角.求证: B (1)AB1⊥平面AAC; (2)AB1II平面AC1C
导航 【典型例题2】如图,在多面体ABC-A1B1C1中,四边形A1ABB1 是正方形,AB=AC,BC= 𝟐AB,B1C1 𝟏 𝟐 BC,二面角 A1-AB-C 是直二面角.求证: (1)A1B1⊥平面AA1C; (2)AB1∥平面A1C1C

导航 证明:.二面角A1AB-C是直二面角, .∴,平面AABB1⊥平面ABC 又四边形A1ABB1是正方形,'AA1LAB .∴AA1⊥平面ABC ∴AA1⊥AC 又AB=AC,BC=V2AB, ∴.∠CAB=90°,即AC⊥AB. .∴AB,AC,AA1两两互相垂直
导航 证明:∵二面角A1 -AB-C是直二面角, ∴平面A1ABB1⊥平面ABC. 又四边形A1ABB1是正方形,∴AA1⊥AB. ∴AA1⊥平面ABC. ∴AA1⊥AC. 又 AB=AC,BC= 𝟐AB, ∴∠CAB=90° ,即AC⊥AB. ∴AB,AC,AA1两两互相垂直