§3-2力矩转动惯量定轴转动定律 一、力矩 F对0点的力矩:M=干×F M=rFsin a 0 M Mz 转动平面 沿z轴分量为对z轴 力矩M2 让美下觉返同速
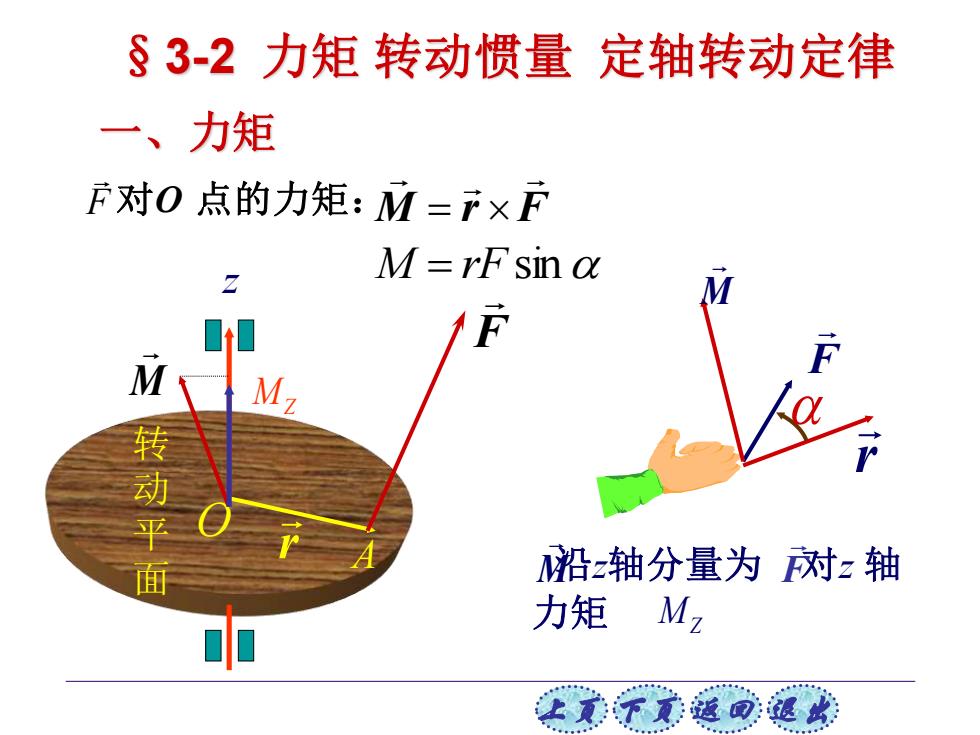
上页 下页 返回 退出 z O 转 动 平 面 r A F M r F M Z M 沿z轴分量为 对z 轴 力矩 MZ F M M = rF sin M r F F 对O 点的力矩: = 一、力矩 §3-2 力矩 转动惯量 定轴转动定律
力不在转动平面内 M=TxF =F×(匠+E) =r×F+r×F, 转动 产×F只能引起轴的 平面 变形,对转动无贡献。 注:(1)在定轴动问题 中,如不加说明,所指的 力矩是指力在转动平面内 的分力对转轴的力矩。 上美不意通可退欢
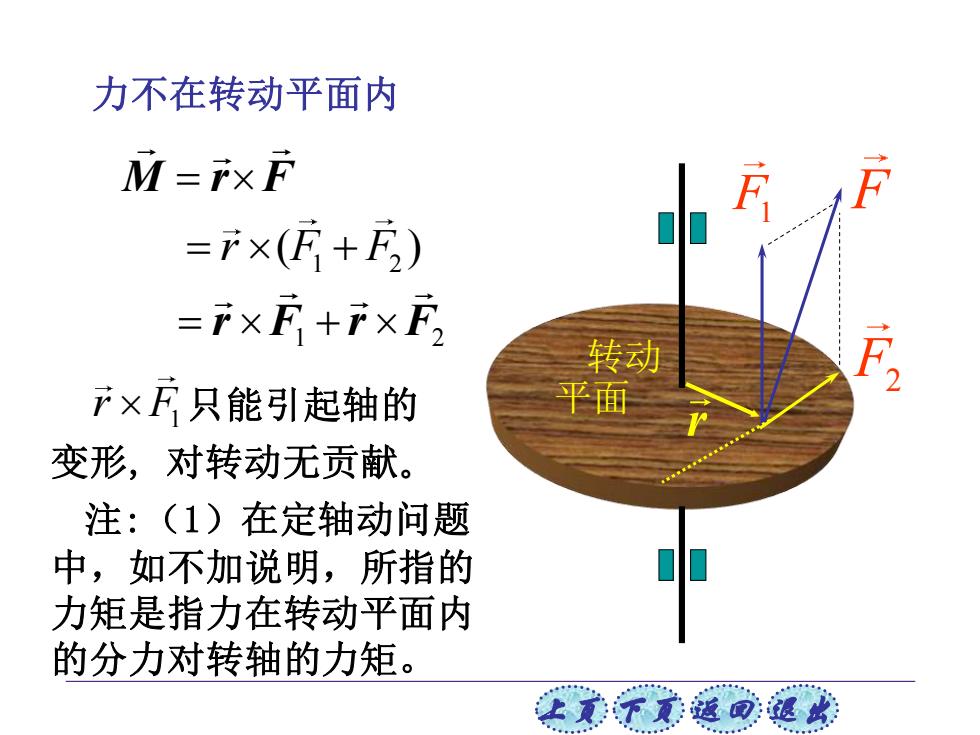
上页 下页 返回 退出 力不在转动平面内 注:(1)在定轴动问题 中,如不加说明,所指的 力矩是指力在转动平面内 的分力对转轴的力矩。 M r F = 只能引起轴的 变形, 对转动无贡献。 1 r F 转动 平面 F1 F F2 1 2 = + r F F ( ) 1 F2 r F r = + r
(2)M.=rF,sina=F,d d=rS转轴到力作用线 的距离,称为力臂。 (3)F对转轴的力矩为零, 转动 在定轴转动中不予考虑。 平面 (4)在转轴方向确定后,力对 转轴的力矩方向可用+、-号表示。 让意文滋可退攻
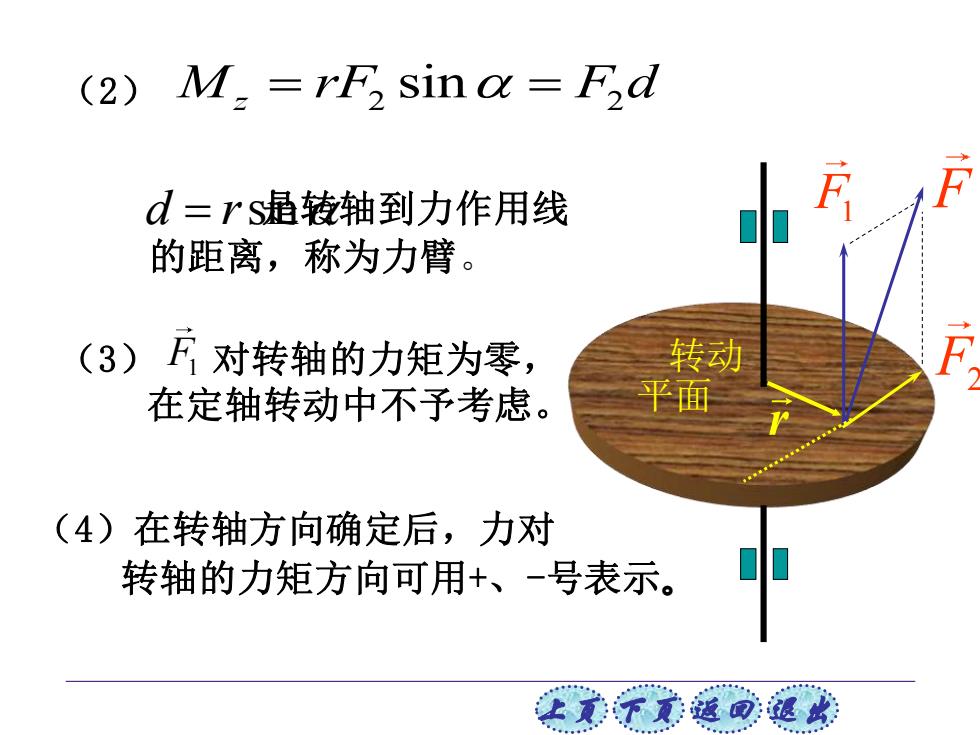
上页 下页 返回 退出 是转轴到力作用线 的距离,称为力臂。 d = rsin 2 2 (2) M rF F d z = = sin (3) F1 对转轴的力矩为零, 在定轴转动中不予考虑。 (4)在转轴方向确定后,力对 转轴的力矩方向可用+、-号表示。 转动 平面 F1 F F2 r
二、 刚体转动的角量描述 1.角坐标 描写刚体转动位置的物理量。 在转动平面内,过O点作 一极轴,设极轴的正方向 是水平向右,则OP与极轴 之间的夹角为0。 角称为角坐标(或角位置)。 角坐标为标量,但可有正负。 让贰子家通可退此
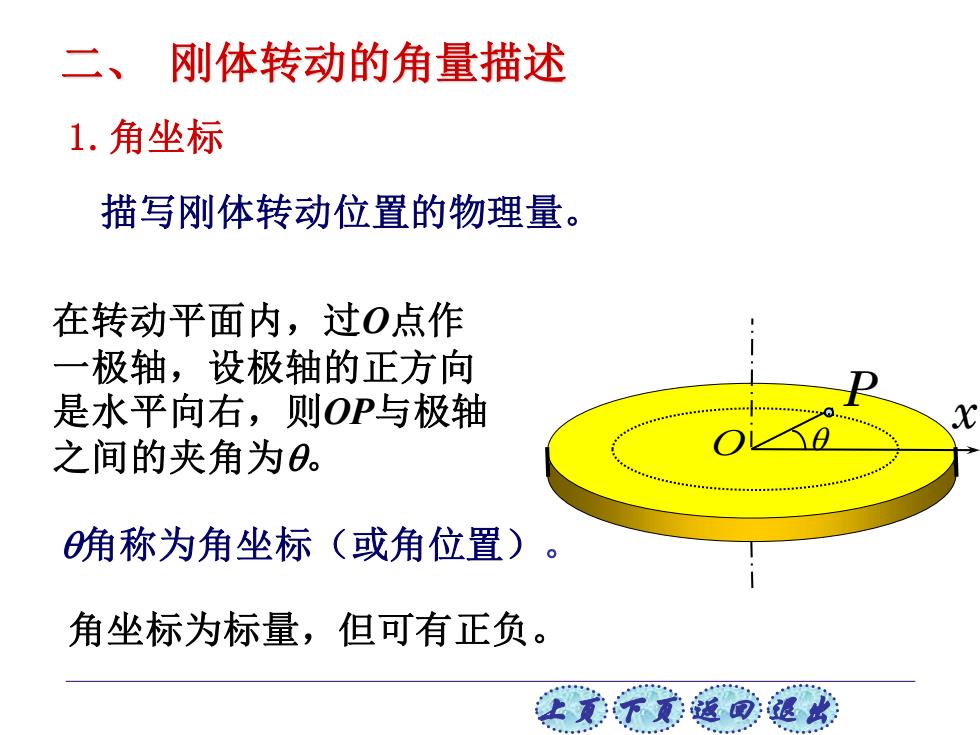
上页 下页 返回 退出 O 描写刚体转动位置的物理量。 P x 在转动平面内,过O点作 一极轴,设极轴的正方向 是水平向右,则OP与极轴 之间的夹角为。 角称为角坐标(或角位置)。 角坐标为标量,但可有正负。 二、 刚体转动的角量描述 1.角坐标
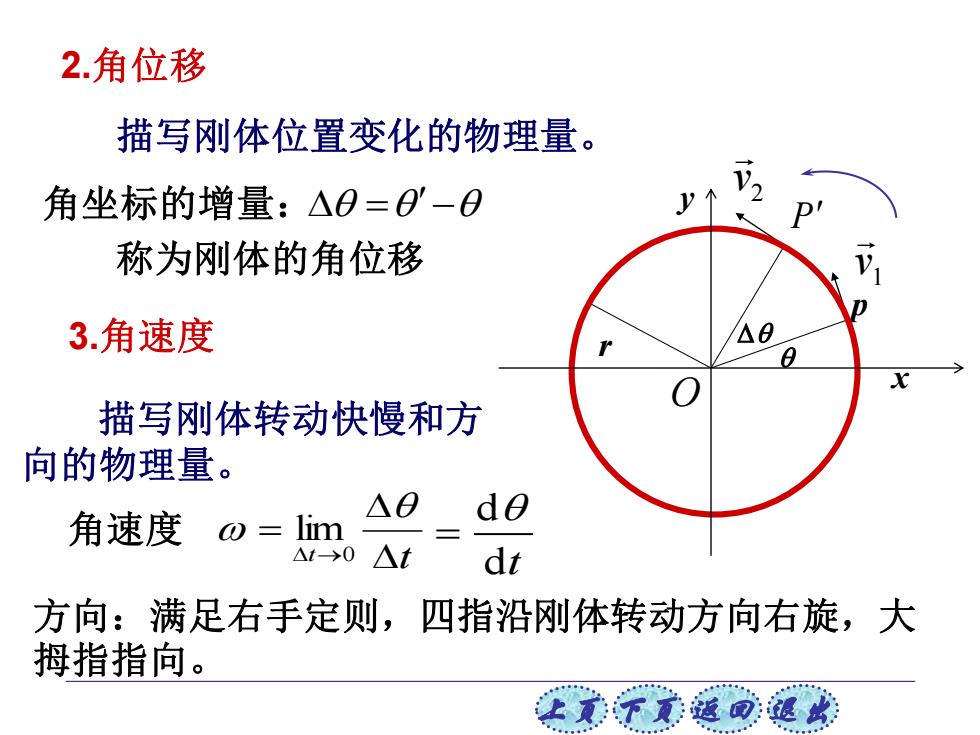
2.角位移 描写刚体位置变化的物理量。 角坐标的增量:△0=0-0 V2 D 称为刚体的角位移 3.角速度 描写刚体转动快慢和方 向的物理量。 角速度o=lim de △t->0 △t dt 方向:满足右手定则,四指沿刚体转动方向右旋,大 拇指指向。 让美下觉返同速
上页 下页 返回 退出 描写刚体位置变化的物理量。 角坐标的增量: =− 称为刚体的角位移 p P 2 v 1 v r 描写刚体转动快慢和方 向的物理量。 t t = → 0 lim d dt 角速度 = 方向:满足右手定则,四指沿刚体转动方向右旋,大 拇指指向。 2.角位移 3.角速度 x y O