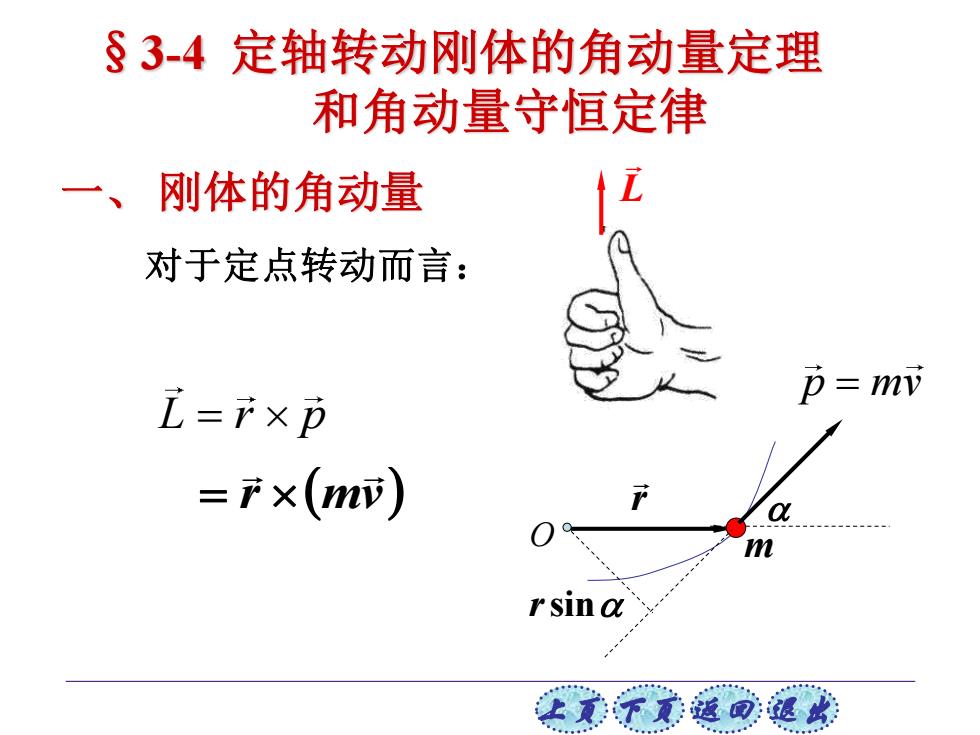
§3-4定轴转动刚体的角动量定理 和角动量守恒定律 一、 刚体的角动量 对于定点转动而言: 瓦=F×p p=mv =产×(m) rsina 上贰不觉返退此
上页 下页 返回 退出 一、 刚体的角动量 对于定点转动而言: L L r p = r m p mv = rsin O r (mv ) = §3-4 定轴转动刚体的角动量定理 和角动量守恒定律
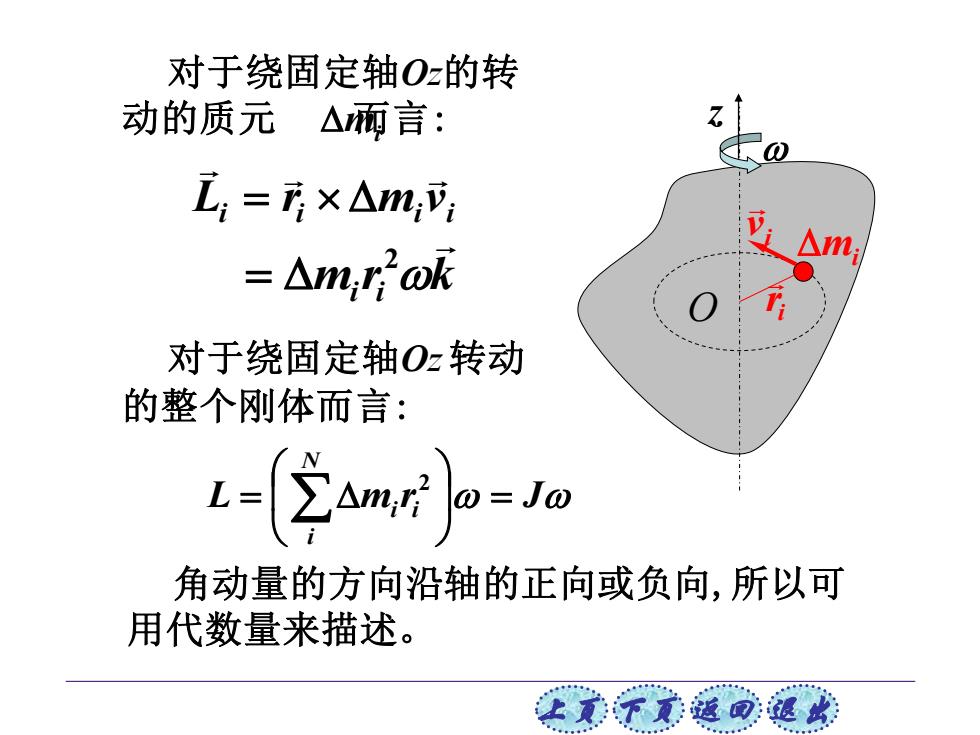
对于绕固定轴Oz的转 动的质元 △而言: Z:=i×△m;: =△,of 对于绕固定轴Oz转动 的整个刚体而言: u-2a加=n 角动量的方向沿轴的正向或负向,所以可 用代数量来描述。 让美下觉返司速此
上页 下页 返回 退出 L i i i i L r m v = mi ri k 2 = 对于绕固定轴Oz转动 的整个刚体而言: 对于绕固定轴Oz的转 动的质元 而言: mi L m r J N i i i = = 2 角动量的方向沿轴的正向或负向,所以可 用代数量来描述。 i r mi i v z O

二、定轴转动刚体的角动量定理 do M= d(Jo)dL dt dr 微分形式:Mdt=d(Jo)=dL 积分形式:Mt=Jw-Jo 或:∫Mdt=L-L 上意不家返可退此
上页 下页 返回 退出 d d M J t = d ( ) d J t = d d L t = 微分形式:M t J L d d d = = ( ) 0 0 d t t M t J J = − 积分形式: 0 0 d t t M t L L = − 或 : 二、 定轴转动刚体的角动量定理

三、定轴转动刚体的角动量守恒定律 由定轴转动定理:M= d(Jo) dt 当M=0时 d(J@)=0 dr 即 J0=J00=常量 刚体在定轴转动中,当对转轴的合外力矩为 零时,刚体对转轴的角动量保持不变,这一规律 就是定轴转动的角动量守恒定律。 让美觉返司退
上页 下页 返回 退出 d( ) d J M t = 当 M=0 时 刚体在定轴转动中,当对转轴的合外力矩为 零时,刚体对转轴的角动量保持不变, 这一规律 就是定轴转动的角动量守恒定律。 由定轴转动定理: d( ) 0 d J t = 即 J = J0 0 =常量 三、 定轴转动刚体的角动量守恒定律

讨论: a.对于绕固定转轴转动的刚体,因J保持不变, 当合外力矩为零时,其角速度恒定。 当M.=0时,J=常 0=常量 量 b.若系统由若干个刚体构成,当合外力矩为零时,系 统的角动量依然守恒。J大→小,J小→ 当M。=0时,L=J1@,+J2@2=常量
上页 下页 返回 退出 a.对于绕固定转轴转动的刚体,因J保持不变, 当合外力矩为零时,其角速度恒定。 J =常 量 =常量 b.若系统由若干个刚体构成,当合外力矩为零时,系 统的角动量依然守恒。J 大→ 小,J 小→ 大 。 L J J z = + = 1 1 2 2 常量 讨论: 0 当 M z = 时, 0 当 M z = 时