
§4-4狭义相对论动力学基础 通过前面的讨论,我们知道在不同惯性系内,时 空坐标遵守洛伦兹变换关系,所以要求物理规律符合 相对性原理,也就是要求它们在洛伦兹变换下保持不 变。牛顿运动方程对伽利略是不变式,对洛伦兹变换 不是不变式。那么,牛顿力学里一系列物理概念,在 相对论中都面临着重新定义的问题。如何定义? 重新定义物理量的原则: (1)受到对应原则的限制,即当速度远远小于光速 时,新定义的物理量必须趋于经典物理中对 应的量。 (2)尽量保持基本守恒定律成立。 (3) 逻辑上的自洽性。 让美觉返司退
上页 下页 返回 退出 通过前面的讨论,我们知道在不同惯性系内,时 空坐标遵守洛伦兹变换关系,所以要求物理规律符合 相对性原理,也就是要求它们在洛伦兹变换下保持不 变。牛顿运动方程对伽利略是不变式,对洛伦兹变换 不是不变式。那么,牛顿力学里一系列物理概念,在 相对论中都面临着重新定义的问题。如何定义? 重新定义物理量的原则 : (1)受到对应原则的限制,即当速度远远小于光速 时,新定义的物理量必须趋于经典物理中对 应的量。 (2) 尽量保持基本守恒定律成立。 (3) 逻辑上的自洽性。 §4-4 狭义相对论动力学基础
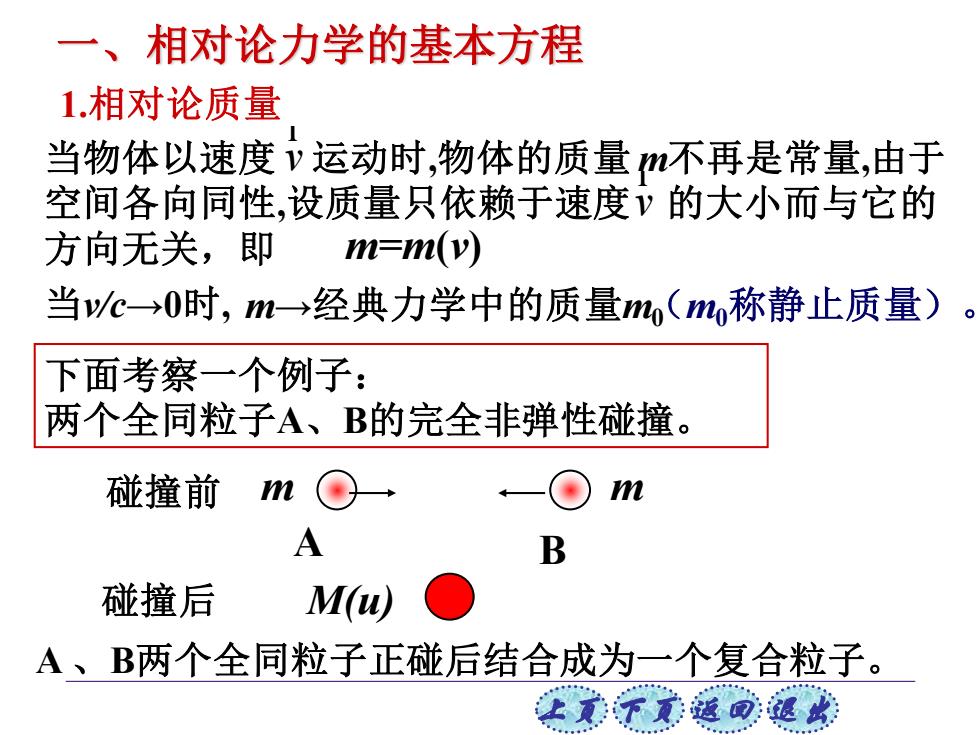
一、相对论力学的基本方程 1.相对论质量 当物体以速度v运动时,物体的质量不再是常量,由于 空间各向同性,设质量只依赖于速度y的大小而与它的 方向无关,即 m=m(v) 当c0时,m→经典力学中的质量m(m,称静止质量) 下面考察一个例子: 两个全同粒子A、B的完全非弹性碰撞。 碰撞前 m A 碰撞后 M A、B两个全同粒子正碰后结合成为一个复合粒子。 王意子返回道球
上页 下页 返回 退出 1.相对论质量 下面考察一个例子: 两个全同粒子A、B的完全非弹性碰撞。 m=m(v) (m0称静止质量)。 M(u) A m B 碰撞前 m 碰撞后 当v/c→0时, m→经典力学中的质量m0 , A 、B两个全同粒子正碰后结合成为一个复合粒子。 一、相对论力学的基本方程 当物体以速度 运动时,物体的质量 m不再是常量,由于 空间各向同性,设质量只依赖于速度 的大小而与它的 方向无关,即 v r v r
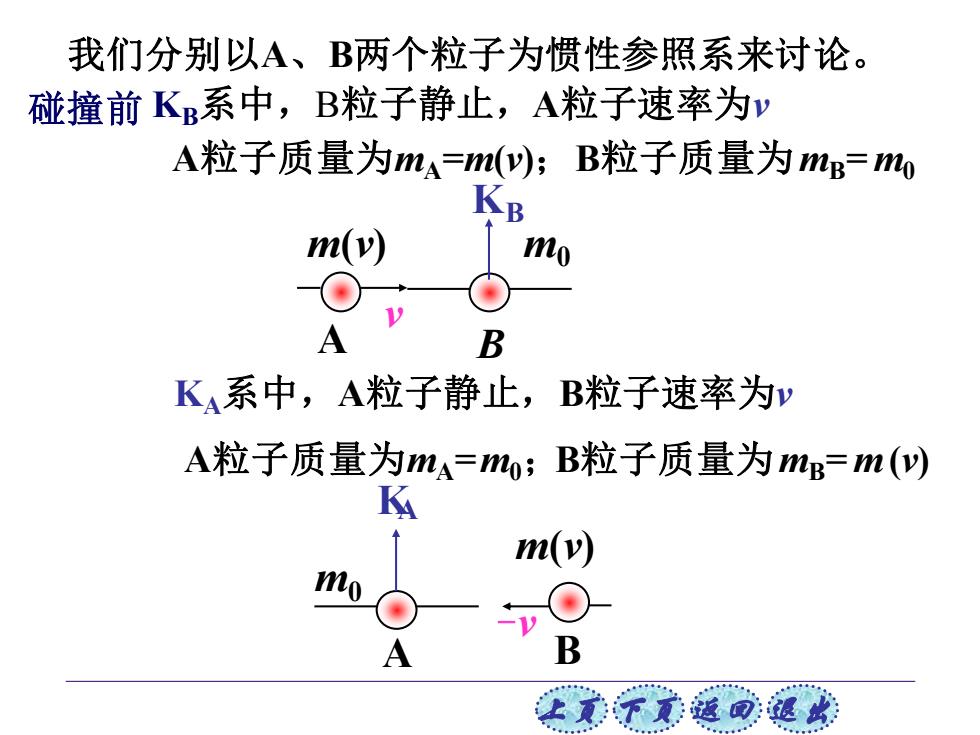
我们分别以A、B两个粒子为惯性参照系来讨论。 碰撞前K系中,B粒子静止,A粒子速率为y A粒子质量为mA=m(y);B粒子质量为mB=mo KB m(v) mo A B K系中,A粒子静止,B粒子速率为 A粒子质量为mA=mo;B粒子质量为mB=m() K m(v) mo A 让美下觉返同速
上页 下页 返回 退出 碰撞前 B KB m(v) A v m0 KA A B m0 m(v) -v 我们分别以A、B两个粒子为惯性参照系来讨论。 KB系中,B粒子静止,A粒子速率为v , A粒子质量为mA=m(v);B粒子质量为mB= m0 KA系中,A粒子静止,B粒子速率为v , A粒子质量为mA=m0;B粒子质量为mB= m (v)
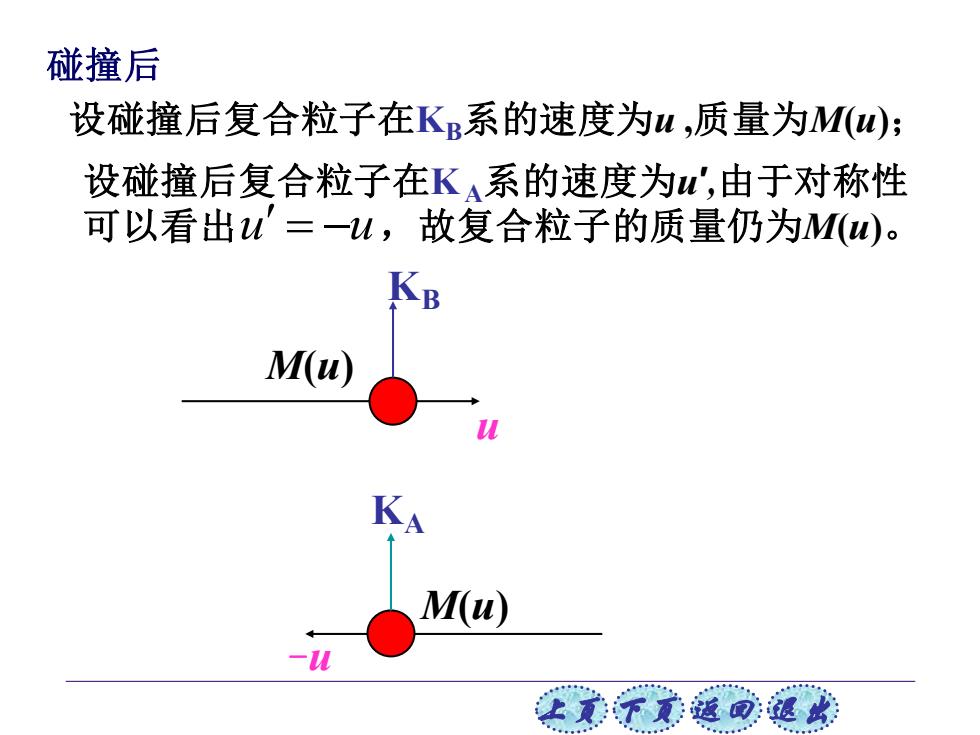
碰撞后 设碰撞后复合粒子在K系的速度为u,质量为M(u); 设碰撞后复合粒子在K系的速度为',由于对称性 可以看出u=-u,故复合粒子的质量仍为M(0)。 KB M(u) KA Mu) 正意子元道回退此
上页 下页 返回 退出 碰撞后 u M(u) KB M(u) -u KA 设碰撞后复合粒子在KB系的速度为u ,质量为M(u); 设碰撞后复合粒子在K A系的速度为u ′ ,由于对称性 可以看出 u u = − ,故复合粒子的质量仍为M(u)

根据动量守恒和质量守恒定律可以得到 m(v)v=M(u)u-(1) m(v)+m=M(u)-(2) M四)_-m)+m=1+m='-(3) m(v) m(v) m(v)u 根据洛伦兹速度变换公式可得 u-v w'=-u= 1-uv/c2 -(4) y=1+V1-v21c2 -(5) u m(v)= mo 相对论质速关系 V1-21c2 上文不美返回退球
上页 下页 返回 退出 根据动量守恒和质量守恒定律可以得到 根据洛伦兹速度变换公式可得 相对论质速关系 m v v M u u ( ) ( ) (1) = − − − 0 m v m M u ( ) ( ) (2) + = − − − 0 ( ) ( ) ( ) ( ) M u m v m m v m v + = 0 1 ( ) m m v = + (3) v u = − − 2 ' (4) 1 / u v u u uv c − = − = − − − − 2 2 1 1 / (5) v v c u = + − − − − 0 2 2 ( ) 1 / m m v v c = −