§3-3定轴转动中的功能关系 一、力矩的功 力矩的功:当刚体在外力矩作用下绕定轴转 动而发生角位移时,就称力矩对刚体作功。 力F对P点作功: dA-F.dr =Fds cos(π/2-p) =Fdssin o ds=rdo 让美下觉返司速此
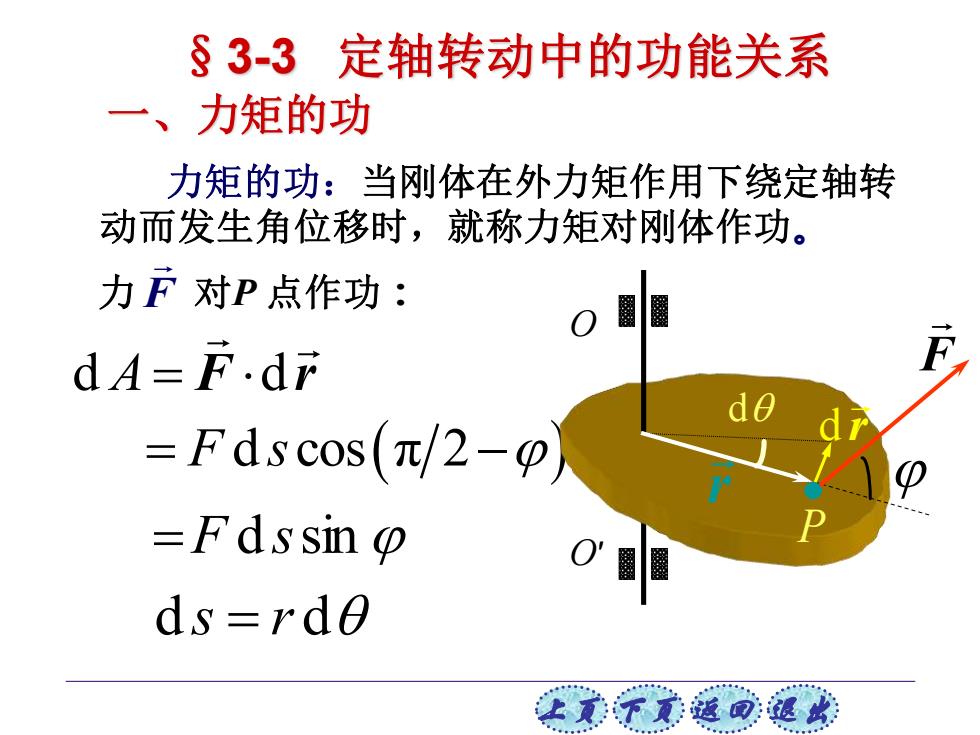
上页 下页 返回 退出 力矩的功:当刚体在外力矩作用下绕定轴转 动而发生角位移时,就称力矩对刚体作功。 力 F 对P 点作功: F r d A = d =F d ssin = − F s d cos(π 2 ) d s = r d O′ O d r F r d P §3-3 定轴转动中的功能关系 一、力矩的功
因Frsin o=M 故dA=MdO 力矩作功: A=∫Md6=心Md0 对于刚体定轴转动 情形,因质点间无相对 位移,任何一对内力作 功为零。 正贰子元道同退此
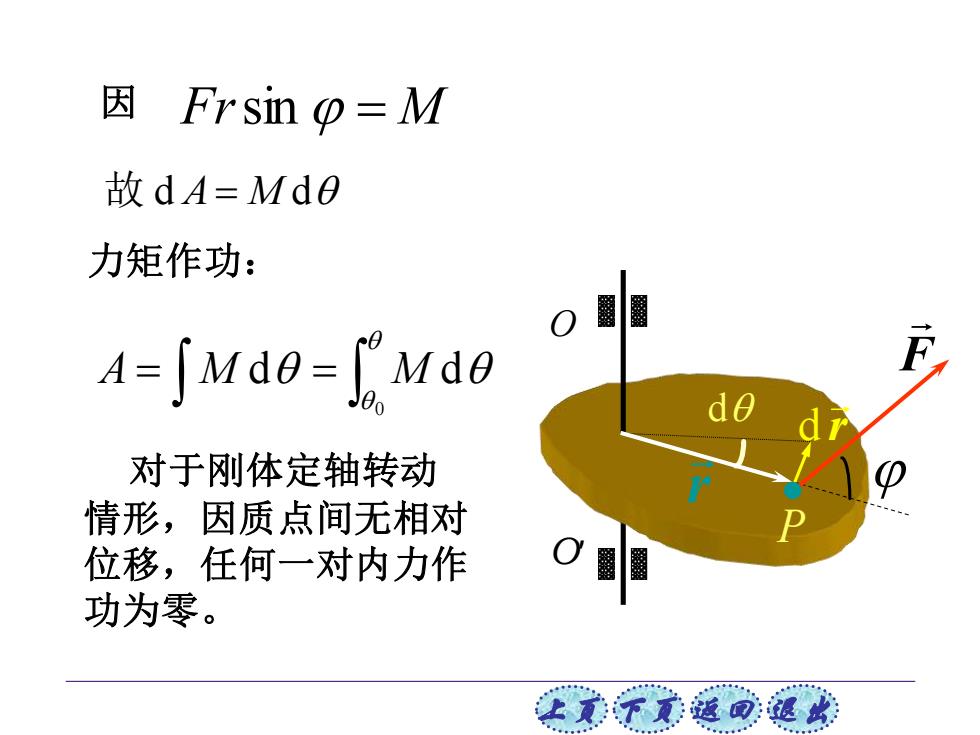
上页 下页 返回 退出 因 Frsin = M 故 d d A M= = = 0 A M d M d 力矩作功: 对于刚体定轴转动 情形,因质点间无相对 位移,任何一对内力作 功为零。 O′ O d r F r d P

二、刚体的转动动能 刚体的转动动能应该是组成刚体的各个质点 的动能之和。设刚体中第个质点的质量为△m, 速度为y,则该质点的动能为 1 △m, 2 刚体做定轴转动时,各质点的角速度相同。 设质点△m离轴的垂直距离为y,则它的线速度 v:=ar 因此整个刚体的动能为 E=∑4mg=)(∑am)o 上觉子觉道司退欢
上页 下页 返回 退出 2 2 1 i i m v 因此整个刚体的动能为 刚体的转动动能应该是组成刚体的各个质点 的动能之和。设刚体中第i个质点的质量为 , 速度为 ,则该质点的动能为 mi i v 刚体做定轴转动时,各质点的角速度相同。 设质点 mi 离轴的垂直距离为 ri ,则它的线速度 ( ) 2 2 2 k 1 1 2 2 E m v m r = = i i i i i i v =r 二、 刚体的转动动能

式中∑△m,是刚体对转轴的转动惯量2所以 上式写为 1 上式中的动能是刚体因转动而具有的动能,因 此叫刚体的转动动能。 三、定轴转动的动能定理 总外力矩对刚体所作的功为A=M0 与此对应的动能增量为 b-jJa AE=2J,2 转动的动能定理 =0=J,2-Jm
上页 下页 返回 退出 2 k 1 2 E J = 上式中的动能是刚体因转动而具有的动能,因 此叫刚体的转动动能。 式中 是刚体对转轴的转动惯量 ,所以 上式写为 2 miri J 总外力矩对刚体所作的功为 2 1 A Md = 2 1 2 2 2 1 1 1 d 2 2 A M J J = = − 2 2 k 2 1 1 1 2 2 与此对应的动能增量为 = − E J J 三、定轴转动的动能定理 转动的动能定理

四、刚体的重力势能 对于一个不太大的质量为m的物体,它的重力 势能应是组成刚体的各个质点的重力势能之和 即 E。=∑Amgh=g∑△m,h 质心高度为 2=∑4mh n 可得 E。=mghc 若只有保守力作功 E=mgh+Jo2=常量 2 让美下觉返司速此
上页 下页 返回 退出 E mgh p = C 即 质心高度为 i i C m h h m = 对于一个不太大的质量为 的物体,它的重力 势能应是组成刚体的各个质点的重力势能之和 m 1 2 2 若只有保守力作功 E mgh J = + = C 常量 四、刚体的重力势能 可得