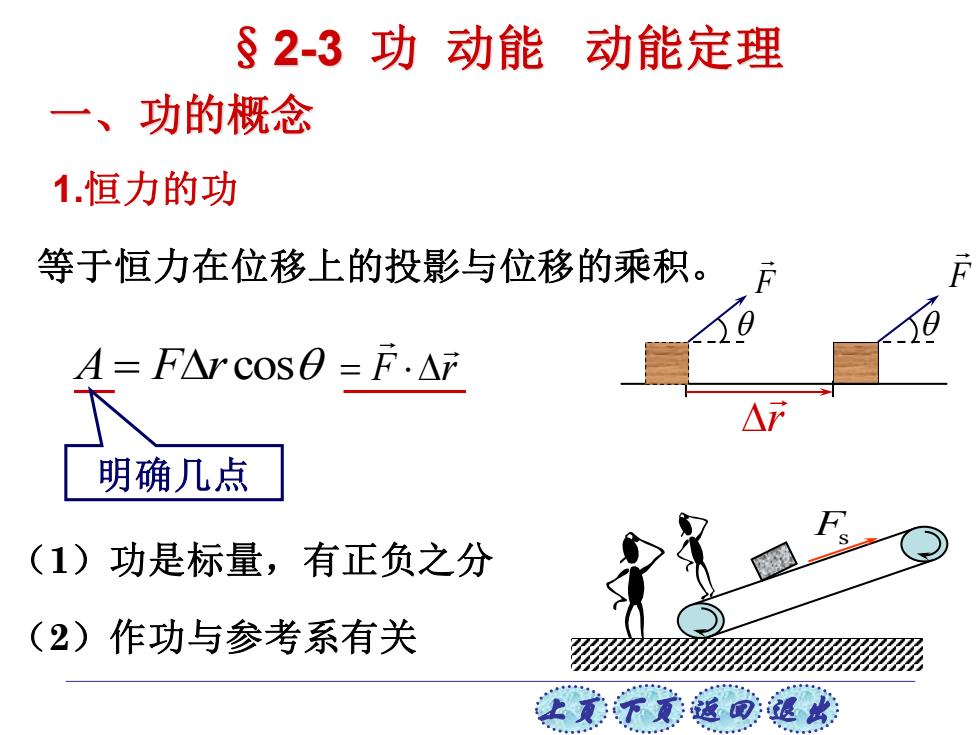
§2-3功动能 动能定理 一、功的概念 1.恒力的功 等于恒力在位移上的投影与位移的乘积。 A=FAr cos0=F.△F 明确几点 (1)功是标量,有正负之分 (2)作功与参考系有关 王美下美菠回:退收
上页 下页 返回 退出 F 等于恒力在位移上的投影与位移的乘积。 r A = Fr cos F r = F (1)功是标量,有正负之分 (2)作功与参考系有关 一、功的概念 1.恒力的功 明确几点 Fs §2-3 功 动能 动能定理

2.变力的功 物体在变力的作用 辉堡屦松A个金 下从运动到b。 怎样计算这个力 的功呢? 采用微元分割法 让意了意返可退收
上页 下页 返回 退出 b a 物体在变力的作用 下从a运动到b。 怎样计算这个力 的功呢? 采用微元分割法 2.变力的功
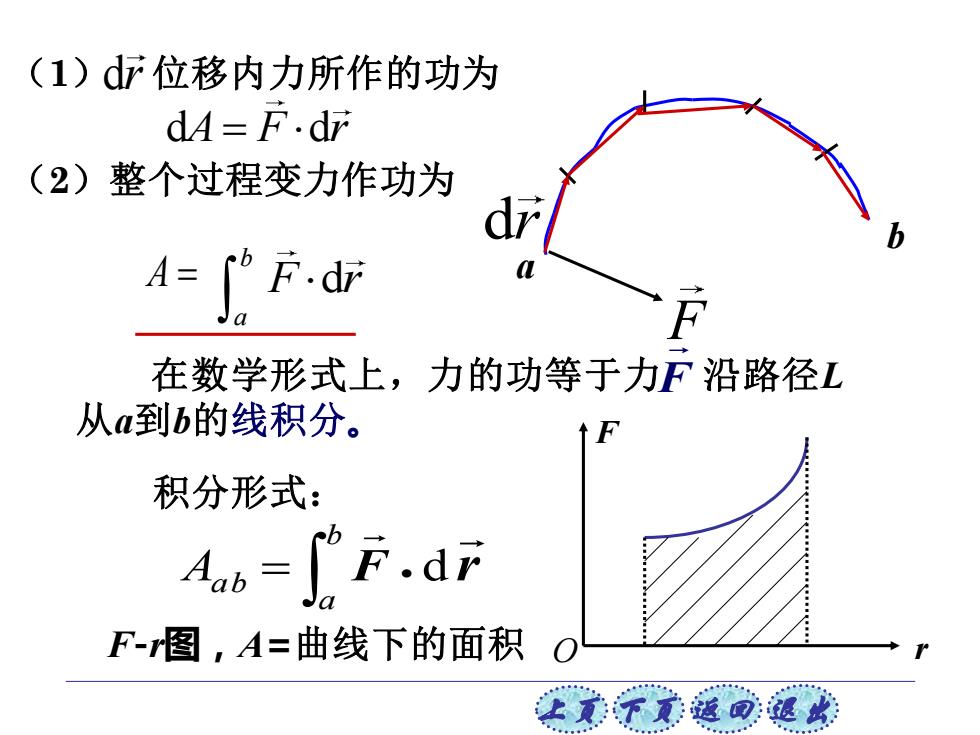
(1)d位移内力所作的功为 dA=F.dr (2)整个过程变力作功为 1=心F. 在数学形式上,力的功等于力F沿路径L 从a到b的线积分。 积分形式: oo= F-图,A=曲线下的面积 让美下元道司退此
上页 下页 返回 退出 F b a dr (1) dr 位移内力所作的功为 d d A F r = F r d (2)整个过程变力作功为 b a A = 积分形式: F r • d = b a Aa b 在数学形式上,力的功等于力 沿路径L 从a到b的线积分。 F F-r图,A=曲线下的面积 F O r

直角坐标系: 受力 F=Fi+Fj+Fk (N) 元位移 dr =dxi +dyj+dzk (m) 元功 dA=Fdx+F,dy+Fdz 总功 Ab=JFdr+∫Fdy+∫Fd正 自然坐标系: 46=∫rds F.d=(Fe+F).dse=Fds 让意子意通回退块
上页 下页 返回 退出 直角坐标系: d d d d A F x F y F z = + + x y z d d d b b b a a a x y z ab x y z x y z A F x F y F z = + + 总功 (N) F F i F j F k = + + x y z d d d d (m) r xi yj zk = + + 元功 受力 元位移 自然坐标系: t d b a s ab s A F s = t t n n t F r F e F e se = + d ( ) d t = F s d

3.合力的功 A6=心F.d=(+E++F)d 4.功率 =A+4++4,=∑4 (1)平均功率P= △A △t △A d (2)功率P=lim 0△t di 恒力的功率: P=F.v d1 P =京可 dt dt 江美觉返司退
上页 下页 返回 退出 (1)平均功率 t A P = (2) 功率 d d A P t = 恒力的功率: t A P t = →0 lim d d A t = d d r F t = F v = P F v = 1 2 d ( ) d b b ab n a a A F r F F F r = = + ++ 1 2 n n i i = + + + = A A A A 3.合力的功 4.功 率