
§2-2动量定理 动量守恒定律 一、动量定理 重写牛顿第二定律的微分形式 Fdt-dp 考虑一过程,时间从到2,两端积分 Fdt=∫d方=p2-p 左侧积分表示力对时间的累积量,叫做冲量。 于是得到积分形式 亚=币2-p 江觉子觉返司退欢
上页 下页 返回 退出 重写牛顿第二定律的微分形式 = 2 1 2 1 d d p p F p t t t 考虑一过程,时间从t1到t2,两端积分 F p dt = d p2 p1 = − 一、 动量定理 左侧积分表示力对时间的累积量,叫做冲量。 = 2 1 d t t I F t 于是得到积分形式 2 1 I p p = − §2-2 动量定理 动量守恒定律

这就是质点的动量定理:物体在运动过程中所受 到的合外力的冲量,等于该物体动量的增量。 动量定理的几点说明: (1)冲量的方向: 冲量的方向一般不是某一瞬时力的方向,而是 所有元冲量F的合矢量∫疗d的方向。 (2)在直角坐标系中将矢量方程改为标量方程 (Is =Sh Fx dt=mvzx -mvis I,=∫F,dt=y2y-my I.=5 F:dt=mv2:-mvi: 让意了意返可退收
上页 下页 返回 退出 这就是质点的动量定理:物体在运动过程中所受 到的合外力的冲量,等于该物体动量的增量。 动量定理的几点说明: (1)冲量的方向: 冲量 的方向一般不是某一瞬时力 的方向,而是 所有元冲量 的合矢量 的方向。 I Fi F dt 2 1 d t t F t (2)在直角坐标系中将矢量方程改为标量方程 x x t I x t Fx t mv2 mv1 2 1 = d = − y y t I y t Fy t mv2 mv1 2 1 = d = − z z t I z t F z t mv2 mv1 2 1 = d = −

(3)动量定理在打击或碰撞问题中用来求平均力。 打击或碰撞,力的方向保持 不变,曲线与轴所包围的面积就 是t到t2这段时间内力雨冲量的 大小,根据改变动量的等效性, 得到平均力。 将积分用平 均力代替 FasF 动量定 理写为 FAI=AP 平均力写为 斥-炉 △t 平均力大小:F= t-t 江美觉返司退
上页 下页 返回 退出 (3)动量定理在打击或碰撞问题中用来求平均力。 t 2 t 1 t − F 打击或碰撞,力 的方向保持 F 不变,曲线与t轴所包围的面积就 是t1到t2这段时间内力 的冲量的 大小,根据改变动量的等效性, 得到平均力。 F F F t p = 2 1 t t F t F t d p F t = 将积分用平 均力代替 动量定 理写为 平均力写为 2 1 2 1 d t t F t F t t = − 平均力大小:
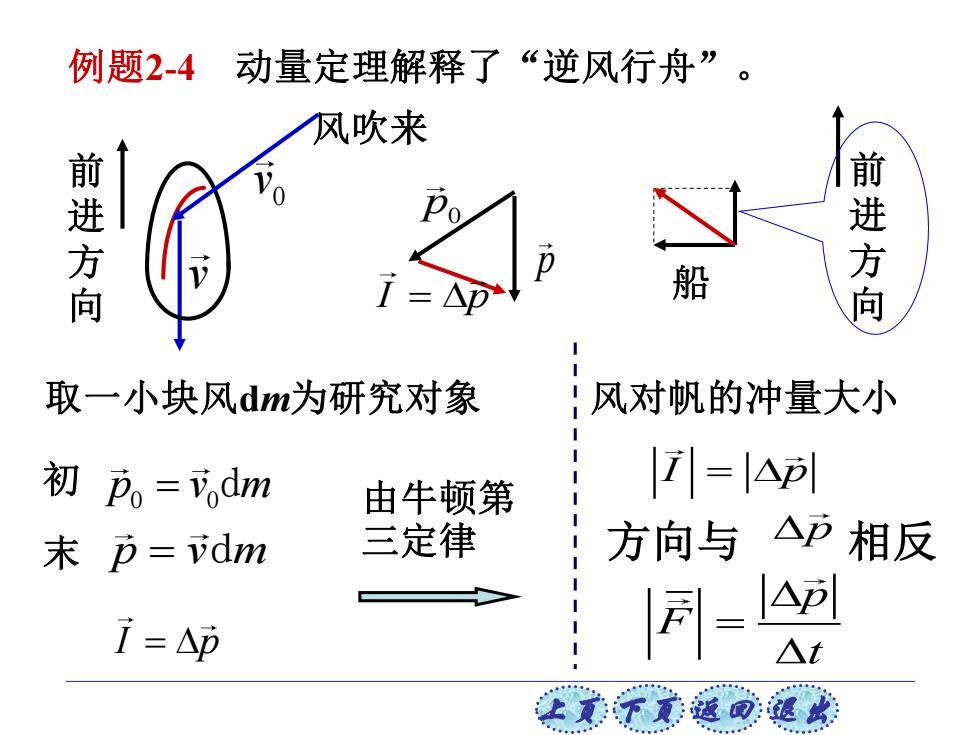
例题2-4动量定理解释了“逆风行舟”。 风吹来 进方 前进方 船 取一小块风dm为研究对象 !风对帆的冲量大小 初p。=d山m 由牛顿第 |=lA列 末币=dm 三定律 方向与 △p相反 AP 1=Ap △t
上页 下页 返回 退出 例题2-4 动量定理解释了“逆风行舟”。 船 前 进 方 向 风吹来 取一小块风dm为研究对象 0 v v p0 p I p = I p = 0 0 初 p v m = d 末 p v m = d 由牛顿第 三定律 前 进 方 向 风对帆的冲量大小 I p = 方向与 p 相反 p F t =

例题2-5质量=3t的重锤,从高度h=1.5m处自由落 到受锻压的工件上,工件发生形变。如果作用的时间 (1)=0.1s,(2)=0.01s。试求锤对工件的平均冲力。 解:以重锤为研究对象,分析受力,作受力图: 解法一锤对工件的冲力变化范 围很大,采用平均冲力计算,其反 作用力用平均支持力代替。 在竖直方向利用动量定理,取竖直 向上为正。 (F-mg)t =mv-mvo 初状态动量为m√2gh 末状态动量为0 美子元道回:退来
上页 下页 返回 退出 例题2-5 质量m=3t的重锤,从高度h=1.5m处自由落 到受锻压的工件上,工件发生形变。如果作用的时间 (1)t=0.1s, (2)t=0.01s。试求锤对工件的平均冲力。 解:以重锤为研究对象,分析受力,作受力图: 解法一 锤对工件的冲力变化范 围很大,采用平均冲力计算,其反 作用力用平均支持力代替。 在竖直方向利用动量定理,取竖直 向上为正。 N 0 ( ) F mg t mv mv − = − 初状态动量为 m gh 2 末状态动量为0 FN mg