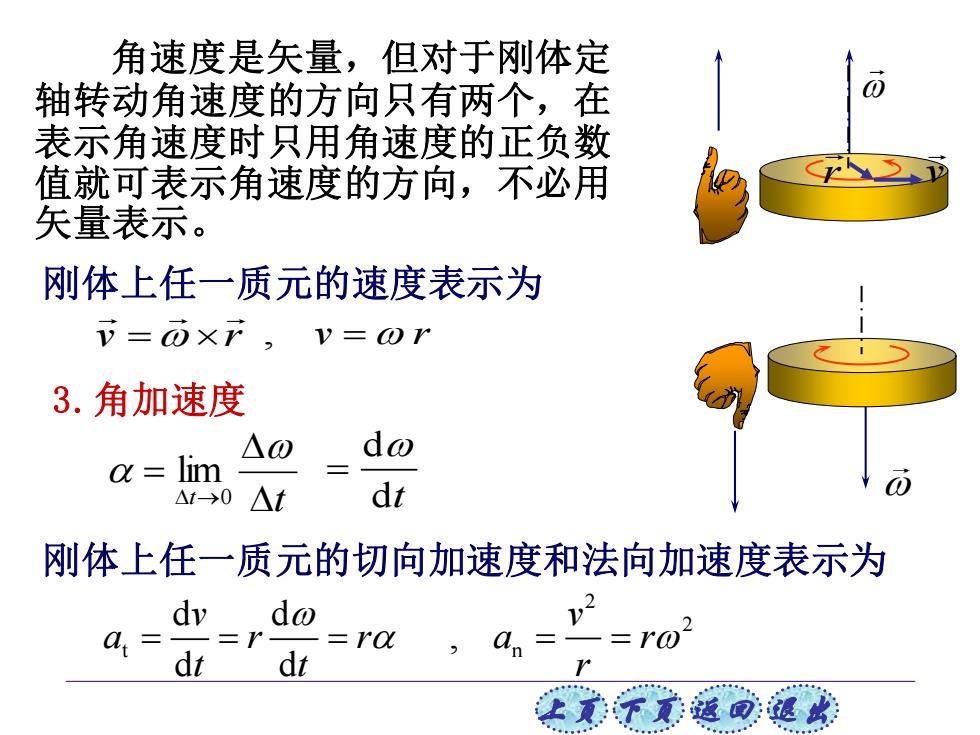
角速度是矢量,但对于刚体定 轴转动角速度的方向只有两个,在 表示角速度时只用角速度的正负数 值就可表示角速度的方向,不必用 矢量表示。 刚体上任一质元的速度表示为 V=而×F,V=ωr 3.角加速度 △⊙ d a lim △t-→0△t dt 刚体上任一质元的切向加速度和法向加速度表示为 dy do a -=r0, dt dt an=-=ro2
上页 下页 返回 退出 角速度是矢量,但对于刚体定 轴转动角速度的方向只有两个,在 表示角速度时只用角速度的正负数 值就可表示角速度的方向,不必用 矢量表示。 刚体上任一质元的速度表示为 v r = v r t t = → 0 lim d dt = , v = r t d d d d v a r r t t = = = 刚体上任一质元的切向加速度和法向加速度表示为 2 2 n , v a r r = = 3.角加速度
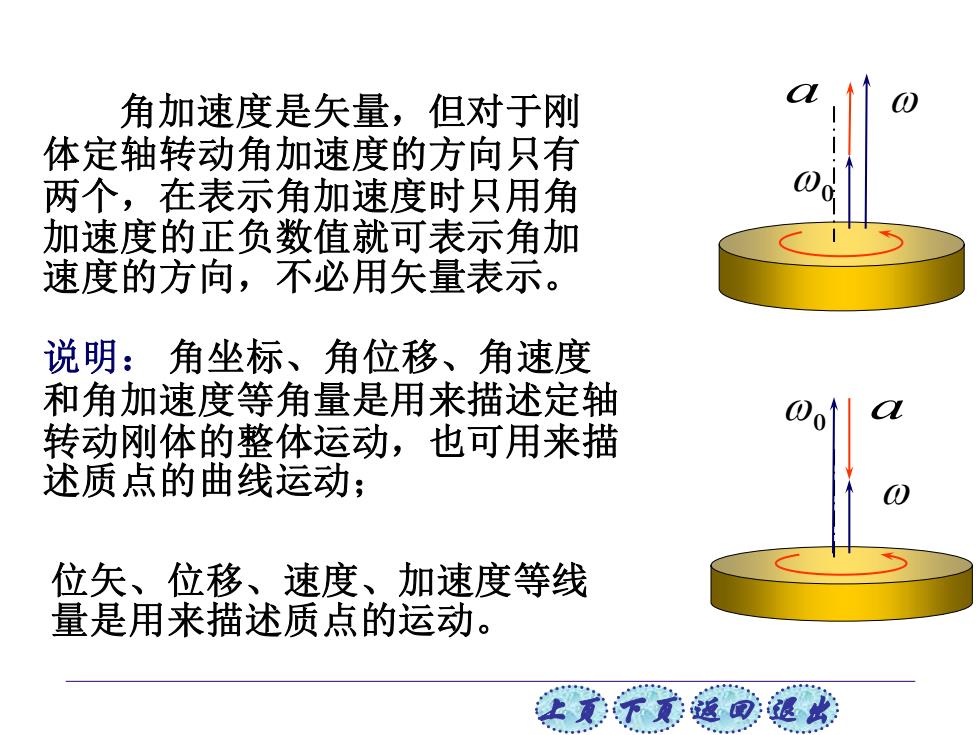
角加速度是矢量,但对于刚 体定轴转动角加速度的方向只有 两个,在表示角加速度时只用角 加速度的正负数值就可表示角加 速度的方向,不必用矢量表示。 说明:角坐标、角位移、角速度 和角加速度等角量是用来描述定轴 转动刚体的整体运动,也可用来描 述质点的曲线运动; 位矢、位移、速度、加速度等线 量是用来描述质点的运动。 让美子觉返同速
上页 下页 返回 退出 a 0 0 a 角加速度是矢量,但对于刚 体定轴转动角加速度的方向只有 两个,在表示角加速度时只用角 加速度的正负数值就可表示角加 速度的方向,不必用矢量表示。 说明: 角坐标、角位移、角速度 和角加速度等角量是用来描述定轴 转动刚体的整体运动,也可用来描 述质点的曲线运动; 位矢、位移、速度、加速度等线 量是用来描述质点的运动
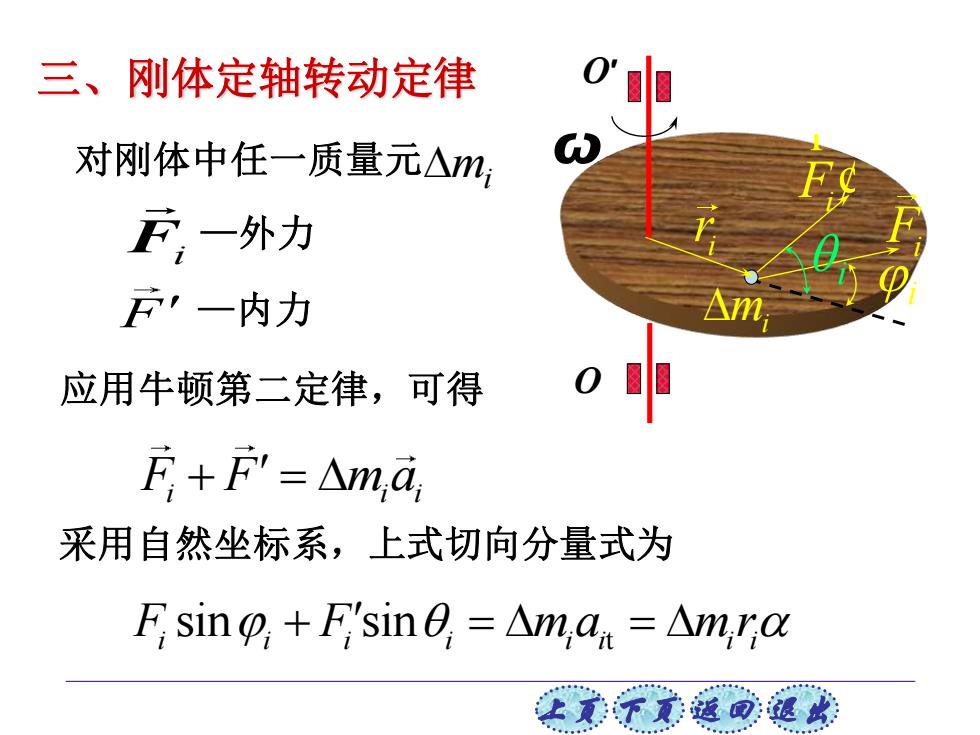
三、刚体定轴转动定律 对刚体中任一质量元△m 云一外力 云,一内力 应用牛顿第二定律,可得 E+F'=△m,a, 采用自然坐标系,上式切向分量式为 F;sing,+E'sin8,=△m,a.=△m,o 让贰不觉返回退
上页 下页 返回 退出 应用牛顿第二定律,可得 ω O Fi Fi ¢ r i i mi i r 对刚体中任一质量元 mi Fi —外力 F —内力 F F m a i i i + = 采用自然坐标系,上式切向分量式为 t sin sin F F m a m r i i i i i i i i + = = 三、刚体定轴转动定律 O′