
2。矩阵及其元素的赋值 ·赋值就是把数赋予代表变量的标识符。MATLAB中的变量或常量 都代表矩阵,标量应看做1×1阶的矩阵。矩阵的值放在方括号 中,同一行中各元素之间以逗号或空格分开,不同的行则以分 号隔开,语句的结尾可用回车符或逗 号,此时会立即显示运算 结果。如果不希望显示结果,就以分号结尾。此时运算仍然执 行,只是不显示。例如输入语句 ·a=[123;456;789] 则显示结果为 a=123 456 789 。 元素也可以用表达式代替,如输入: X=[-1.3,sqrt(3),(1+2+3)/5*4] 。 结果为 ● x=-1.3000 1.7321 4.8000
2。 矩阵及其元素的赋值 • 赋值就是把数赋予代表变量的标识符。MATLAB中的变量或常量 都代表矩阵,标量应看做1 1阶的矩阵。矩阵的值放在方括号 中,同一行中各元素之间以逗号或空格分开,不同的行则以分 号隔开,语句的结尾可用回车符或逗号,此时会立即显示运算 结果。如果不希望显示结果,就以分号结尾。此时运算仍然执 行,只是不显示。例如输入语句 • a=[1 2 3;4 5 6;7 8 9] • 则显示结果为 • a= 1 2 3 • 4 5 6 • 7 8 9 • 元素也可以用表达式代替,如输入: • x=[-1.3,sqrt(3),(1+2+3)/5*4] • 结果为 • x=-1.3000 1.7321 4.8000

变量下标的使用 变量中的元素序号用“()”中的数字(也称为下标) 来注明,一维矩阵(也称数组或向量)中的元素用 个下标表示,二维的矩阵可有行号和列号两个下标 数,以逗号分开。用户可以单独给元素赋值,如果 赋值元素的下标超出了原来矩阵的大小,、则矩阵的 行列会自动扩展。如在上述x的赋值语句之后键入: · x(5)=abs(x(1) ·得: ·×=-1.30001.7321 4.8000 01.3000 ·给全行赋值,可用冒号。例如,给a的第5行赋值。 可键入: ·a(4,3)=6.5;a(5,:)=[5,4,3]
变量下标的使用 • 变量中的元素序号用“( )”中的数字(也称为下标) 来注明,一维矩阵(也称数组或向量)中的元素用一 个下标表示,二维的矩阵可有行号和列号两个下标 数,以逗号分开。用户可以单独给元素赋值,如果 赋值元素的下标超出了原来矩阵的大小,则矩阵的 行列会自动扩展。如在上述x的赋值语句之后键入: • x(5)=abs(x(1)) • 得: • x =-1.3000 1.7321 4.8000 0 1.3000 • 给全行赋值,可用冒号。例如,给a的第5行赋值。 可键入: • a(4,3)=6.5; a(5, :)=[5,4,3]

矩阵赋值(续) 得:a=1.0000 2.0000 3.0000 4.0000 5.0000 6.0000 7.0000 8.0000 9.0000 ● 0 0 6.5000 ● 5.0000 4.0000 3.0000 可见,跳空的元素x(4),a(4,1),a(4,2)被自动赋值为0。这种 自动扩展维数的功能只适用于赋值语句。在其他语句中若出现 超维调用的情况,、系统将瓮出出错提示。一个矩阵的所有元素 都要用同样的格式显示,因为出现了a(4,3)=6.5,所以a的所有 元素都有了小数点。 把a的第二,,四行及第一,三列交点上的元素取出,构成一个新 矩阵b。可键入: b=a([2,4],[1,3]) ·得:b= 4.0000 6.0000 0 6.5000
矩阵赋值(续) 得:a =1.0000 2.0000 3.0000 • 4.0000 5.0000 6.0000 • 7.0000 8.0000 9.0000 • 0 0 6.5000 • 5.0000 4.0000 3.0000 • 可见,跳空的元素x(4),a(4,1),a(4,2)被自动赋值为0。这种 自动扩展维数的功能只适用于赋值语句。在其他语句中若出现 超维调用的情况,系统将给出出错提示。一个矩阵的所有元素 都要用同样的格式显示,因为出现了a(4,3)=6.5,所以a的所有 元素都有了小数点。 • 把a的第二,四行及第一,三列交点上的元素取出,构成一个新 矩阵b。可键入: b = a([2,4],[1,3]) • 得:b = 4.0000 6.0000 0 6.5000

空矩阵和矩阵元素的删除 ·要删除a中的第二、四、五行,可利用空矩阵([)的概念。 键入: a([2,4,5],:)=[] ·得:a= 123 789 洼意,“窑阵”是指婆有云春的矩阵兵对凭但金阵赋以 值门,就是使它的元素都消尖獐。这完全不茼宇“零矩库分 后者是云素存在,一尽是基数值为零而己。可以看出,空矩阵是 佞矩库减缩时宋可缺少的瓣卷。 a'为矩阵a的共轭转置命令。若a是实数矩阵,则它就是矩阵a的 转置。此处键入a',得到: ans 17 28 39
空矩阵和矩阵元素的删除 • 要删除a中的第二、四、五行,可利用空矩阵([ ])的概念。 • 键入: a([2,4,5],:)=[ ] • 得:a = 1 2 3 7 8 9 • 注意,“空矩阵”是指没有元素的矩阵。对任何一个矩阵赋以 值[ ],就是使它的元素都消失掉。这完全不同于“零矩阵”, 后者是元素存在,只是其数值为零而已。可以看出,空矩阵是 使矩阵减缩时不可缺少的概念。 • a'为矩阵a的共轭转置命令。若a是实数矩阵,则它就是矩阵a的 转置。此处键入a',得到: ans = 1 7 2 8 3 9
3)基本赋值矩阵 为了方便给矩阵赋值,MATLAB提供了一些最 常用的基本矩阵如下表所示。 zeros(m,n) 全0矩阵(mxn阶) linspace 均分向量(1xn维数组) ones(m,n) 全1矩阵(mxn阶) logspace 对数均分向量(1×n维) 本 rand(m,n) mxn随机数矩阵 meshgrid 画三维曲面时的X,Y 网格 正态随机数矩阵 阵 randn(m,n) (mxn阶) magic(n) 魔方矩阵 eye(n) 单位矩阵(方阵) size(A) 多维矩阵的各维长度 length 维矩阵的长度 diag 提取或建立对角阵 结 fliplr 矩阵左右翻转 tril 取矩阵的左下三角部分 flipud 矩阵上下翻转 triu 取矩阵的右上三角部分 换
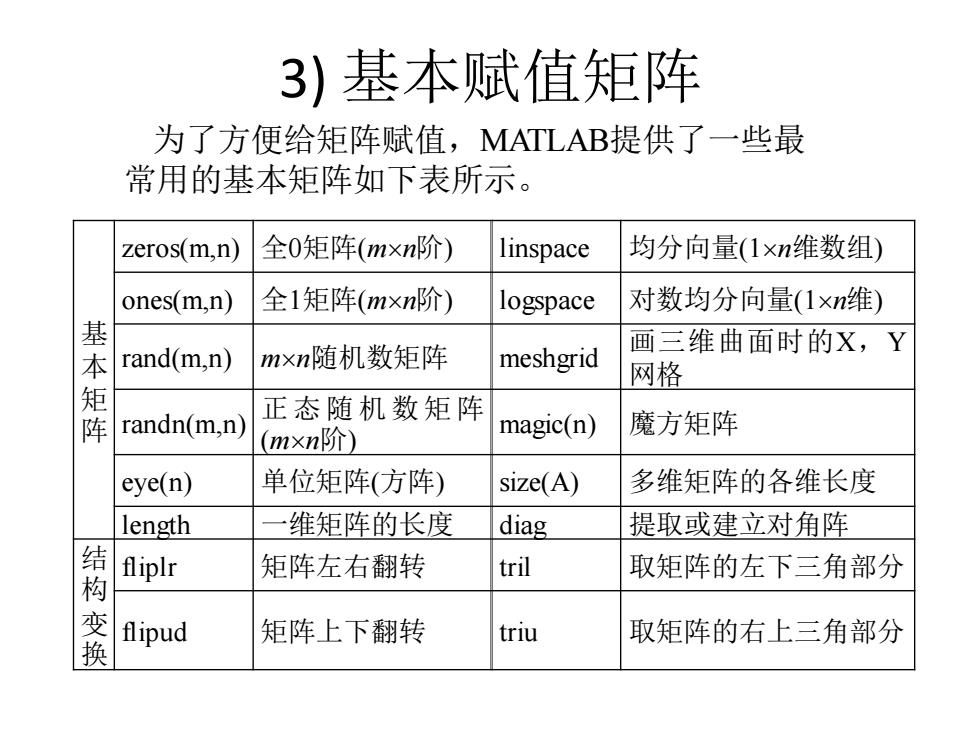
3) 基本赋值矩阵 基 本 矩 阵 zeros(m,n) 全0矩阵(mn阶) linspace 均分向量(1n维数组) ones(m,n) 全1矩阵(mn阶) logspace 对数均分向量(1n维) rand(m,n) mn随机数矩阵 meshgrid 画三维曲面时的X,Y 网格 randn(m,n) 正态随机数矩阵 (mn阶) magic(n) 魔方矩阵 eye(n) 单位矩阵(方阵) size(A) 多维矩阵的各维长度 length 一维矩阵的长度 diag 提取或建立对角阵 结 构 变 换 fliplr 矩阵左右翻转 tril 取矩阵的左下三角部分 flipud 矩阵上下翻转 triu 取矩阵的右上三角部分 为了方便给矩阵赋值,MATLAB提供了一些最 常用的基本矩阵如下表所示