《数字信号处理》课程教学课件（PPT讲稿）ch4_4 双线性变换法

稳定性2 1- z-12/T +sUZS=T 1+2-12/T-s(2 / T +α)2 +?s=o+ jo(2 /T -0)° +02左半平面映射到单位元内。稳定AF系[<11)g<0,统映射为稳定DF系统[-1 虚轴映射到单位圆上2)o=0,[z>13)o>0,右半平面映射到单位圆列外二结论：因果、稳定的AF系统映射为因果、稳定的DF系统

稳定性 1 1 1 2 1      z z T s T s T s z     2 2 s    jw 2 2 2 2 (2 / ) (2 / )  w  w      T T z 1<0, |z|<1 左半平面映射到单位元内。稳定AF系 统映射为稳定DF系统。 20, |z|=1 3>0, |z|>1 虚轴映射到单位圆上 右半平面映射到单位圆外 结论： 因果、稳定的AF系统映射为因果、稳定的DF系统

Q和の的关系Ts1+122 1-zz=S=Ts-1T 1+z令s-jo12(T0)1+ jTaexp( jtan -22= exp(j2tan(T)z=To)1- jTo2exp(-jtan2220Q = 2tantan0=T2<

W和w 的关系 2 1 2 1 Ts Ts z     令s=jw 2 j 1 2 j 1 w w T T z    )) 2 exp( jtan ( )) 2 exp(jtan ( 1 1 w w T T     )) 2 exp(j2tan ( 1 Tw  ) 2 2tan ( 1 wT W  ) 2 tan( 2 W  T w 1 1 1 2 1      z z T s

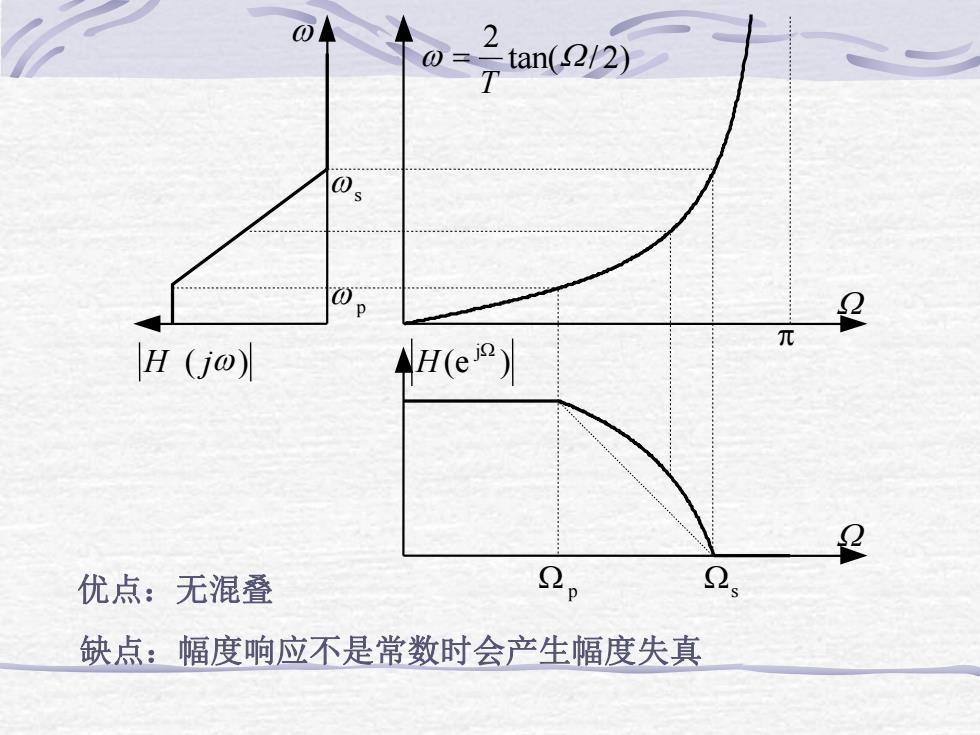
OA20=tan(2/ 2)TOs0pQ元NH(eig)[H (jo)QQs2优点：无混叠/缺点：幅度响应不是常数时会产生幅度失真

tan( / 2) 2  W T w W p ( ) jW H ( jw) H e W p W s W w p w s w 缺点：幅度响应不是常数时会产生幅度失真 优点：无混叠

双线性法设计DF的步骤：1)将数字滤波器的频率指标(Q)由のk=(2/T)tan(2/2转换为模拟滤波器的频率指标のi2）由模拟滤波器的指标设计H（s3)H(s)转换为H(z)H(z)=H(s)2 1-2-1T1+2-1

双线性法设计DF的步骤： 2) 由模拟滤波器的指标设计H (s) 3) H (s)转换为H(z) 1 1 1 2 1 ( ) ( )       z z T s H z H s 1)将数字滤波器的频率指标{Wk}由wk=(2/T)tan(Wk /2) 转换为模拟滤波器的频率指标{wk}

例：用一阶模拟巴特沃思低通滤波器和双线性变换法，设计一个3dB截止频率为2的数字低通滤波器解：设双线性变换中的参数为T2为 0p=二tan(, /2)1)模拟低通滤波器的3dB截率为-pT2)3dB截率为の,的一阶模拟BWLP滤波器为11H(s)=-sTs/0, +1-+12 tan(2, /2)3）由双线性变换得tan(2,/2)(1+ z-l)(1-α) 1+z-1H(z) =1+ tan(2,/2) +(tan(2,/2) - 1)z-2 1-0z-11-tan(Q,/2)α=1+ tan(2,/2)

解：设双线性变换中的参数为T 1)模拟低通滤波器的3dB截率为 tan( / 2) 2 p p T w  W 2)3dB截率为wp的一阶模拟BW LP 滤波器为 1 2tan( / 2) 1 / 1 1 ( )     p p sT s H s W w 3)由双线性变换得 1 1 1 tan(Ω 2) (tan(Ω 2) 1) tan( 2)(1 ) ( )      W   / / z / z H z p p p 1 1 1 1 2 (1 )       z z   1 tan(Ω 2) 1 tan( 2) / / p p   W   例：用一阶模拟巴特沃思低通滤波器和双线性变换法，设计 一个3dB截止频率为Wp的数字低通滤波器