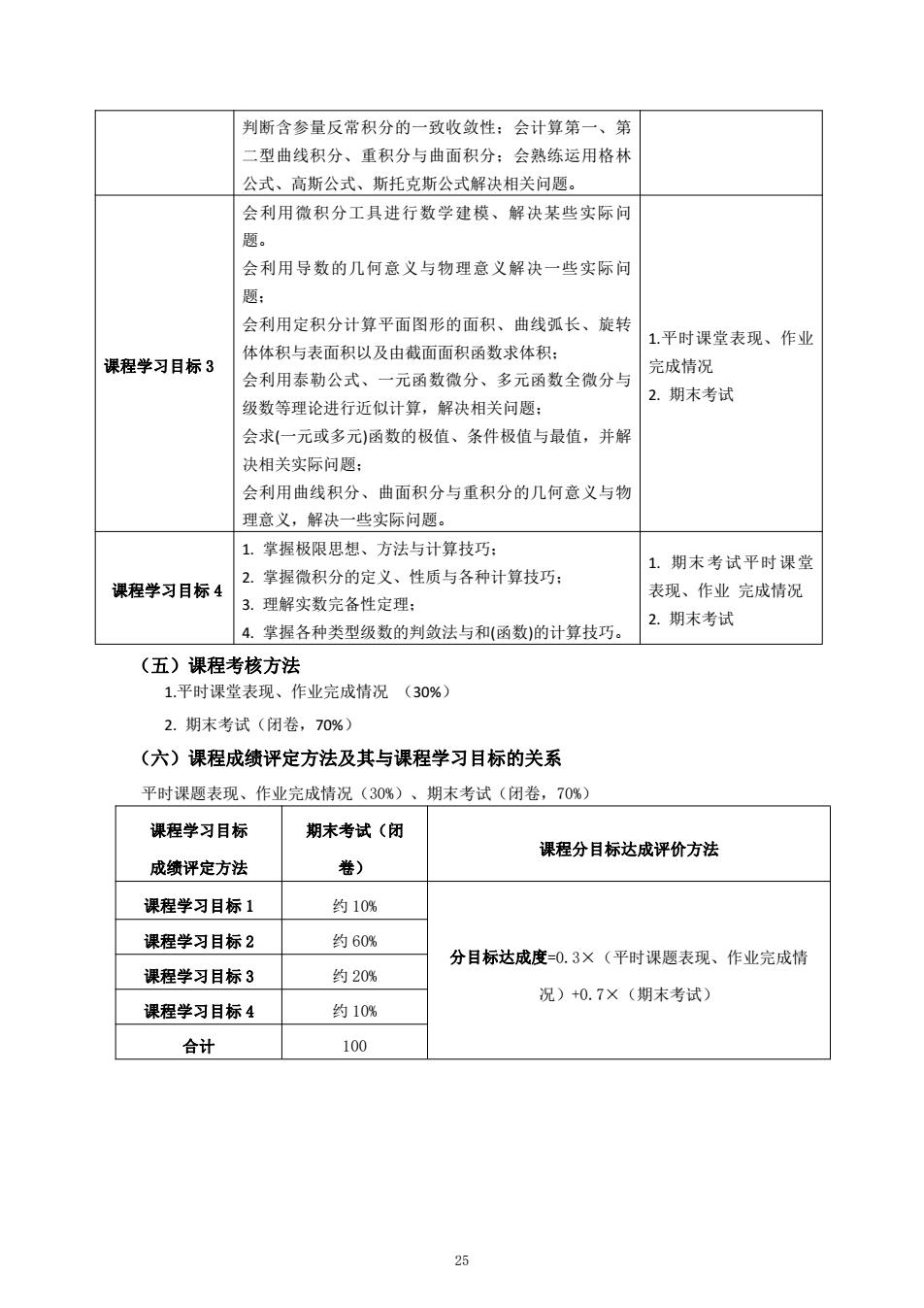
判断含参量反常积分的一致收敛性:会计算第一、第 二型曲线积分、重积分与曲面积分:会熟练运用格林 公式、高斯公式、斯托克斯公式解决相关问题。 会利用微积分工具进行数学建模、解决某些实际问 题。 会利用导数的几何意义与物理意义解决一些实际问 题; 会利用定积分计算平面图形的面积、曲线弧长、旋转 1.平时课堂表现、作业 体体积与表面积以及由截面面积函数求体积: 课程学习目标3 完成情况 会利用泰勒公式、一元函数微分、多元函数全微分与 2.期末考试 级数等理论进行近似计算,解决相关问题: 会求(一元或多元)函数的极值、条件极值与最值,并解 决相关实际问题: 会利用曲线积分、曲面积分与重积分的几何意义与物 理意义,解决一些实际问题。 1.掌握极限思想、方法与计算技巧: 1.期末考试平时课堂 2.掌握微积分的定义、性质与各种计算技巧: 课程学习目标4 表现、作业完成情况 3.理解实数完备性定理: 2.期末考试 4.掌握各种类型级数的判敛法与和(函数)的计算技巧。 (五)课程考核方法 1.平时课堂表现、作业完成情况(30%) 2.期末考试(闭卷,70%) (六)课程成绩评定方法及其与课程学习目标的关系 平时课题表现、作业完成情况(30%)、期末考试(闭卷,70%) 课程学习目标 期末考试(闭 课程分目标达成评价方法 成绩评定方法 卷) 课程学习目标1 约10% 课程学习目标2 约60% 分目标达成度=0.3×(平时课题表现、作业完成情 课程学习目标3 约20% 况)+0.7×(期末考试) 课程学习目标4 约10% 合计 100 25
判断含参量反常积分的一致收敛性;会计算第一、第 二型曲线积分、重积分与曲面积分;会熟练运用格林 公式、高斯公式、斯托克斯公式解决相关问题。 课程学习目标 3 会利用微积分工具进行数学建模、解决某些实际问 题。 会利用导数的几何意义与物理意义解决一些实际问 题; 会利用定积分计算平面图形的面积、曲线弧长、旋转 体体积与表面积以及由截面面积函数求体积; 会利用泰勒公式、一元函数微分、多元函数全微分与 级数等理论进行近似计算,解决相关问题; 会求(一元或多元)函数的极值、条件极值与最值,并解 决相关实际问题; 会利用曲线积分、曲面积分与重积分的几何意义与物 理意义,解决一些实际问题。 1.平时课堂表现、作业 完成情况 2. 期末考试 课程学习目标 4 1. 掌握极限思想、方法与计算技巧; 2. 掌握微积分的定义、性质与各种计算技巧; 3. 理解实数完备性定理; 4. 掌握各种类型级数的判敛法与和(函数)的计算技巧。 1. 期末考试平时课堂 表现、作业 完成情况 2. 期末考试 (五)课程考核方法 1.平时课堂表现、作业完成情况 (30%) 2. 期末考试(闭卷,70%) (六)课程成绩评定方法及其与课程学习目标的关系 平时课题表现、作业完成情况(30%)、期末考试(闭卷,70%) 课程学习目标 成绩评定方法 期末考试(闭 卷) 课程分目标达成评价方法 课程学习目标 1 约 10% 分目标达成度=0.3×(平时课题表现、作业完成情 况)+0.7×(期末考试) 课程学习目标 2 约 60% 课程学习目标 3 约 20% 课程学习目标 4 约 10% 合计 100 25
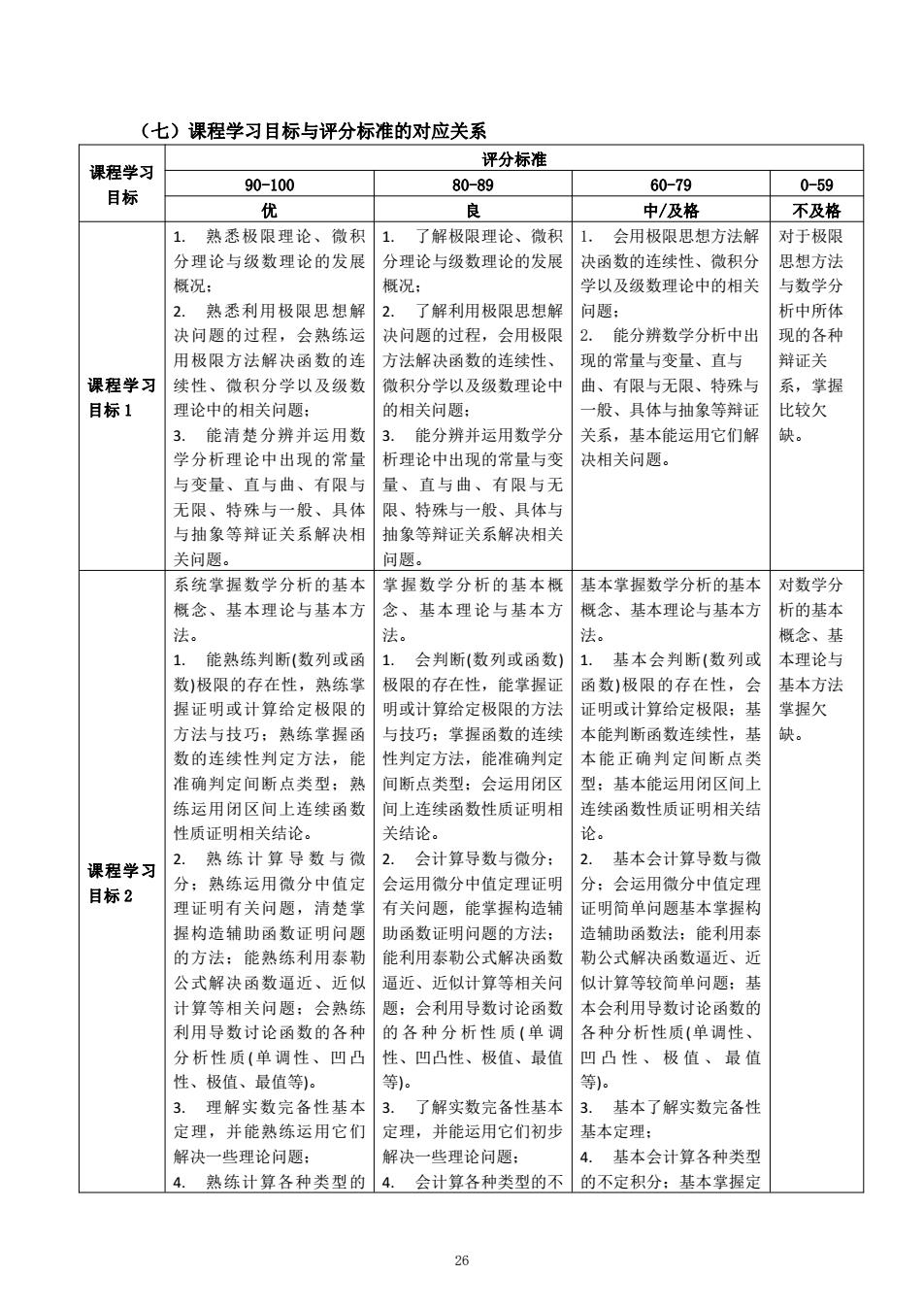
(七)课程学习目标与评分标准的对应关系 评分标准 课程学习 90-100 80-89 60-79 0-59 目标 优 良 中/及格 不及格 1. 熟悉极限理论、微积 1. 了解极限理论、微积 1. 会用极限思想方法解 对于极限 分理论与级数理论的发展 分理论与级数理论的发展 决函数的连续性、微积分 思想方法 概况: 概况: 学以及级数理论中的相关 与数学分 2. 熟悉利用极限思想解 2. 了解利用极限思想解 问题: 析中所体 决问题的过程,会熟练运 决问题的过程,会用极限 2. 能分辨数学分析中出 现的各种 用极限方法解决函数的连 方法解决函数的连续性、 现的常量与变量、直与 辩证关 课程学习 续性、微积分学以及级数 微积分学以及级数理论中 曲、有限与无限、特殊与 系,掌握 目标1 理论中的相关问题: 的相关问题: 一般、具体与抽象等辩证 比较欠 3. 能清楚分辨并运用数 3. 能分辨并运用数学分 关系,基本能运用它们解 缺。 学分析理论中出现的常量 析理论中出现的常量与变 决相关问题。 与变量、直与曲、有限与 量、直与曲、有限与无 无限、特殊与一般、具体 限、特殊与一般、具体与 与抽象等辩证关系解决相 抽象等辩证关系解决相关 关问题。 问题。 系统掌握数学分析的基本 掌握数学分析的基本概 基本掌握数学分析的基本 对数学分 概念、基本理论与基本方 念、基本理论与基本方 概念、基本理论与基本方 析的基本 法。 法。 法。 概念、基 1. 能熟练判断(数列或函 1. 会判断(数列或函数) 1. 基本会判断(数列或 本理论与 数)极限的存在性,熟练掌 极限的存在性,能掌握证 函数)极限的存在性,会 基本方法 握证明或计算给定极限的 明或计算给定极限的方法 证明或计算给定极限:基 掌握欠 方法与技巧:熟练掌握函 与技巧:掌握函数的连续 本能判断函数连续性,基 缺。 数的连续性判定方法,能 性判定方法,能准确判定 本能正确判定间断点类 准确判定间断点类型:熟 间断点类型:会运用闭区 型:基本能运用闭区间上 练运用闭区间上连续函数 间上连续函数性质证明相 连续函数性质证明相关结 性质证明相关结论。 关结论。 论。 2. 熟练计算导数与微 2.会计算导数与微分: 2. 基本会计算导数与微 课程学习 分;熟练运用微分中值定 会运用微分中值定理证明 分:会运用微分中值定理 目标2 理证明有关问题,清楚掌 有关问题,能掌握构造辅 证明简单问题基本掌握构 握构造辅助函数证明问题 助函数证明问题的方法: 造辅助函数法:能利用泰 的方法:能熟练利用泰勒 能利用泰勒公式解决函数 勒公式解决函数逼近、近 公式解决函数逼近、近似 逼近、近似计算等相关问 似计算等较简单问题:基 计算等相关问题:会熟练 题:会利用导数讨论函数 本会利用导数讨论函数的 利用导数讨论函数的各种 的各种分析性质(单调 各种分析性质(单调性、 分析性质(单调性、凹凸 性、凹凸性、极值、最值 凹凸性、极值、最值 性、极值、最值等)。 等)。 等)。 3.理解实数完备性基本 3.了解实数完备性基本 3.基本了解实数完备性 定理,并能熟练运用它们 定理,并能运用它们初步 基本定理: 解决一些理论问题: 解决一些理论问题: 4.基本会计算各种类型 4. 熟练计算各种类型的 4.会计算各种类型的不 的不定积分:基本掌握定 名
(七)课程学习目标与评分标准的对应关系 课程学习 目标 评分标准 90-100 80-89 60-79 0-59 优 良 中/及格 不及格 课程学习 目标 1 1. 熟悉极限理论、微积 分理论与级数理论的发展 概况; 2. 熟悉利用极限思想解 决问题的过程,会熟练运 用极限方法解决函数的连 续性、微积分学以及级数 理论中的相关问题; 3. 能清楚分辨并运用数 学分析理论中出现的常量 与变量、直与曲、有限与 无限、特殊与一般、具体 与抽象等辩证关系解决相 关问题。 1. 了解极限理论、微积 分理论与级数理论的发展 概况; 2. 了解利用极限思想解 决问题的过程,会用极限 方法解决函数的连续性、 微积分学以及级数理论中 的相关问题; 3. 能分辨并运用数学分 析理论中出现的常量与变 量、直与曲、有限与无 限、特殊与一般、具体与 抽象等辩证关系解决相关 问题。 1. 会用极限思想方法解 决函数的连续性、微积分 学以及级数理论中的相关 问题; 2. 能分辨数学分析中出 现的常量与变量、直与 曲、有限与无限、特殊与 一般、具体与抽象等辩证 关系,基本能运用它们解 决相关问题。 对于极限 思想方法 与数学分 析中所体 现的各种 辩证关 系,掌握 比较欠 缺。 课程学习 目标 2 系统掌握数学分析的基本 概念、基本理论与基本方 法。 1. 能熟练判断(数列或函 数)极限的存在性,熟练掌 握证明或计算给定极限的 方法与技巧;熟练掌握函 数的连续性判定方法,能 准确判定间断点类型;熟 练运用闭区间上连续函数 性质证明相关结论。 2. 熟 练 计 算 导 数 与 微 分;熟练运用微分中值定 理证明有关问题,清楚掌 握构造辅助函数证明问题 的方法;能熟练利用泰勒 公式解决函数逼近、近似 计算等相关问题;会熟练 利用导数讨论函数的各种 分析性质(单调性、凹凸 性、极值、最值等)。 3. 理解实数完备性基本 定理,并能熟练运用它们 解决一些理论问题; 4. 熟练计算各种类型的 掌握数学分析的基本概 念、基本理论与基本方 法。 1. 会判断(数列或函数) 极限的存在性,能掌握证 明或计算给定极限的方法 与技巧;掌握函数的连续 性判定方法,能准确判定 间断点类型;会运用闭区 间上连续函数性质证明相 关结论。 2. 会计算导数与微分; 会运用微分中值定理证明 有关问题,能掌握构造辅 助函数证明问题的方法; 能利用泰勒公式解决函数 逼近、近似计算等相关问 题;会利用导数讨论函数 的 各 种 分 析 性 质 ( 单 调 性、凹凸性、极值、最值 等)。 3. 了解实数完备性基本 定理,并能运用它们初步 解决一些理论问题; 4. 会计算各种类型的不 基本掌握数学分析的基本 概念、基本理论与基本方 法。 1. 基本会判断(数列或 函数)极限的存在性,会 证明或计算给定极限;基 本能判断函数连续性,基 本能正确判定间断点类 型;基本能运用闭区间上 连续函数性质证明相关结 论。 2. 基本会计算导数与微 分;会运用微分中值定理 证明简单问题基本掌握构 造辅助函数法;能利用泰 勒公式解决函数逼近、近 似计算等较简单问题;基 本会利用导数讨论函数的 各种分析性质(单调性、 凹 凸 性 、 极 值 、 最 值 等)。 3. 基本了解实数完备性 基本定理; 4. 基本会计算各种类型 的不定积分;基本掌握定 对数学分 析的基本 概念、基 本理论与 基本方法 掌握欠 缺。 26

不定积分:熟练掌握定积 定积分:掌握定积分的概 积分的概念、性质与意 分的概念、性质与意义: 念、 性质与意义:会判断 义:基本会判断函数的可 会判断函数的可积性,掌 函数的可积性,掌握可积 积性,了解可积函数类: 握可积函数类:熟练运用 函数类:会运用微积分基 基本能运用微积分基本定 微积分基本定理证明有关 本定理证明有关积分问 理证明简单的积分问题: 积分问题:熟练运用牛顿 题:能运用牛顿莱布尼 基本会计算定积分与反常 莱布尼茨公式计算定积 茨公式计算定积分:会计 积分,基本能判断反常积 分:会计算反常积分,熟 算反常积分,并判断反常 分的敛散性。 练判断反常积分的敛散 积分的敛散性。 5.基本判断数项级数的 性。 5.会判断数项级数的收 收敛性,函数项级数的一 5.熟练判断数项级数的 敛性,函数项级数的一致 致收敛性:基本能讨论函 收敛性,函数项级数的一 收敛性:会正确讨论函数 数项级数的极限函数的分 致收敛性:会正确讨论函 项级数的极限函数的分析 析性质;能利用一致收敛 数项级数的极限函数的分 性质;能利用一致收敛函 函数项级数的逐项可微与 析性质:能利用一致收敛 数项级数的逐项可微与逐 逐项可积性求解一些简单 函数项级数的逐项可微与 项可积性求解函数项级数 函数项级数的和函数:基 逐项可积性熟练求解函数 的和函数:会讨论幂级数 本会讨论幂级数的收敛情 项级数的和函数:熟练讨 的收敛情况,会求一些幂 况,并会求一些简单幂级 论幂级数的收敛情况,能 级数的和函数,会求一些 数的和函数,基本能求 熟练计算一些幂级数的和 简单函数的幂级数展开 些简单函数的幂级数展开 函数,并求一些简单函数 式:会求函数的傅里叶展 式:基本会求函数的傅里 的幂级数展开式:能熟练 开式,并讨论收敛性。 叶展开式,并讨论收敛 求解函数的傅里叶展开 6.会计算二元函数的重 性。 式,并讨论收敛性。 极限、累次极限:能运用 6. 基本会计算二元函数 6. 能熟练计算二元函数 有界闭域上连续函数性质 的重极限、累次极限:基 的重极限、累次极限:能 证明有关问题。 本能运用有界闭域上连续 熟练运用有界闭域上连续 7. 会计算多元函数与隐 函数性质证明有关问题。 函数性质证明有关问题。 函数(组)的偏导数:会计 7. 基本会计算多元函数 7. 能熟练计算多元函数 算多元函数的全微分:会 与隐函数(组)的偏导数、 与隐函数(组)的偏导数:熟 求解二元函数的极值与最 多元函数的全微分:会求 练计算多元函数的全微 值:会求函数的梯度与方 解简单的二元函数的极值 分:熟练求解二元函数的 向导数:能运用拉格朗日 与最值:基本会求函数的 极值与最值;会求函数的 乘数法求函数的条件极 梯度与方向导数:基本能 梯度与方向导数:能熟练 值。 运用拉格朗日乘数法求函 运用拉格朗日乘数法求函 8. 能正确讨论含参量正 数的条件极值。 数的条件极值。 常积分与含参量反常积分 8.基本会讨论含参量正 8. 能清楚地讨论含参量 的分析性质,并进行计 常积分与含参量反常积分 正常积分与含参量反常积 算:会计算含参量正常积 的分析性质,并进行计 分的分析性质,并进行计 分的导数:会判断含参量 算:基本会计算含参量正 算:能熟练计算含参量正 反常积分的一致收敛性: 常积分的导数:基本会判 常积分的导数:熟练判断 会计算第一、第二型曲线 断含参量反常积分的一致 含参量反常积分的一致收 积分、重积分与曲面积 收敛性:基本会计算第 敛性:能熟练计算第一 分:会运用格林公式、高 第二型曲线积分、重 27
不定积分;熟练掌握定积 分的概念、性质与意义; 会判断函数的可积性,掌 握可积函数类;熟练运用 微积分基本定理证明有关 积分问题;熟练运用牛顿- 莱 布 尼 茨 公 式 计 算 定 积 分;会计算反常积分,熟 练 判 断 反 常 积 分 的 敛 散 性。 5. 熟练判断数项级数的 收敛性,函数项级数的一 致收敛性;会正确讨论函 数项级数的极限函数的分 析性质;能利用一致收敛 函数项级数的逐项可微与 逐项可积性熟练求解函数 项级数的和函数;熟练讨 论幂级数的收敛情况,能 熟练计算一些幂级数的和 函数,并求一些简单函数 的幂级数展开式;能熟练 求 解 函 数 的 傅 里 叶 展 开 式,并讨论收敛性。 6. 能熟练计算二元函数 的重极限、累次极限;能 熟练运用有界闭域上连续 函数性质证明有关问题。 7. 能熟练计算多元函数 与隐函数(组)的偏导数;熟 练 计 算 多 元 函 数 的 全 微 分;熟练求解二元函数的 极值与最值;会求函数的 梯度与方向导数;能熟练 运用拉格朗日乘数法求函 数的条件极值。 8. 能清楚地讨论含参量 正常积分与含参量反常积 分的分析性质,并进行计 算;能熟练计算含参量正 常积分的导数;熟练判断 含参量反常积分的一致收 敛性;能熟练计算第一、 定积分;掌握定积分的概 念、性质与意义;会判断 函数的可积性,掌握可积 函数类;会运用微积分基 本定理证明有关积分问 题;能运用牛顿-莱布尼 茨公式计算定积分;会计 算反常积分,并判断反常 积分的敛散性。 5. 会判断数项级数的收 敛性,函数项级数的一致 收敛性;会正确讨论函数 项级数的极限函数的分析 性质;能利用一致收敛函 数项级数的逐项可微与逐 项可积性求解函数项级数 的和函数;会讨论幂级数 的收敛情况,会求一些幂 级数的和函数,会求一些 简单函数的幂级数展开 式;会求函数的傅里叶展 开式,并讨论收敛性。 6. 会计算二元函数的重 极限、累次极限;能运用 有界闭域上连续函数性质 证明有关问题。 7. 会计算多元函数与隐 函数(组)的偏导数;会计 算多元函数的全微分;会 求解二元函数的极值与最 值;会求函数的梯度与方 向导数;能运用拉格朗日 乘数法求函数的条件极 值。 8. 能正确讨论含参量正 常积分与含参量反常积分 的分析性质,并进行计 算;会计算含参量正常积 分的导数;会判断含参量 反常积分的一致收敛性; 会计算第一、第二型曲线 积分、重积分与曲面积 分;会运用格林公式、高 积分的概念、性质与意 义;基本会判断函数的可 积性,了解可积函数类; 基本能运用微积分基本定 理证明简单的积分问题; 基本会计算定积分与反常 积分,基本能判断反常积 分的敛散性。 5. 基本判断数项级数的 收敛性,函数项级数的一 致收敛性;基本能讨论函 数项级数的极限函数的分 析性质;能利用一致收敛 函数项级数的逐项可微与 逐项可积性求解一些简单 函数项级数的和函数;基 本会讨论幂级数的收敛情 况,并会求一些简单幂级 数的和函数,基本能求一 些简单函数的幂级数展开 式;基本会求函数的傅里 叶展开式,并讨论收敛 性。 6. 基本会计算二元函数 的重极限、累次极限;基 本能运用有界闭域上连续 函数性质证明有关问题。 7. 基本会计算多元函数 与隐函数(组)的偏导数、 多元函数的全微分;会求 解简单的二元函数的极值 与最值;基本会求函数的 梯度与方向导数;基本能 运用拉格朗日乘数法求函 数的条件极值。 8. 基本会讨论含参量正 常积分与含参量反常积分 的分析性质,并进行计 算;基本会计算含参量正 常积分的导数;基本会判 断含参量反常积分的一致 收敛性;基本会计算第 一、第二型曲线积分、重 27
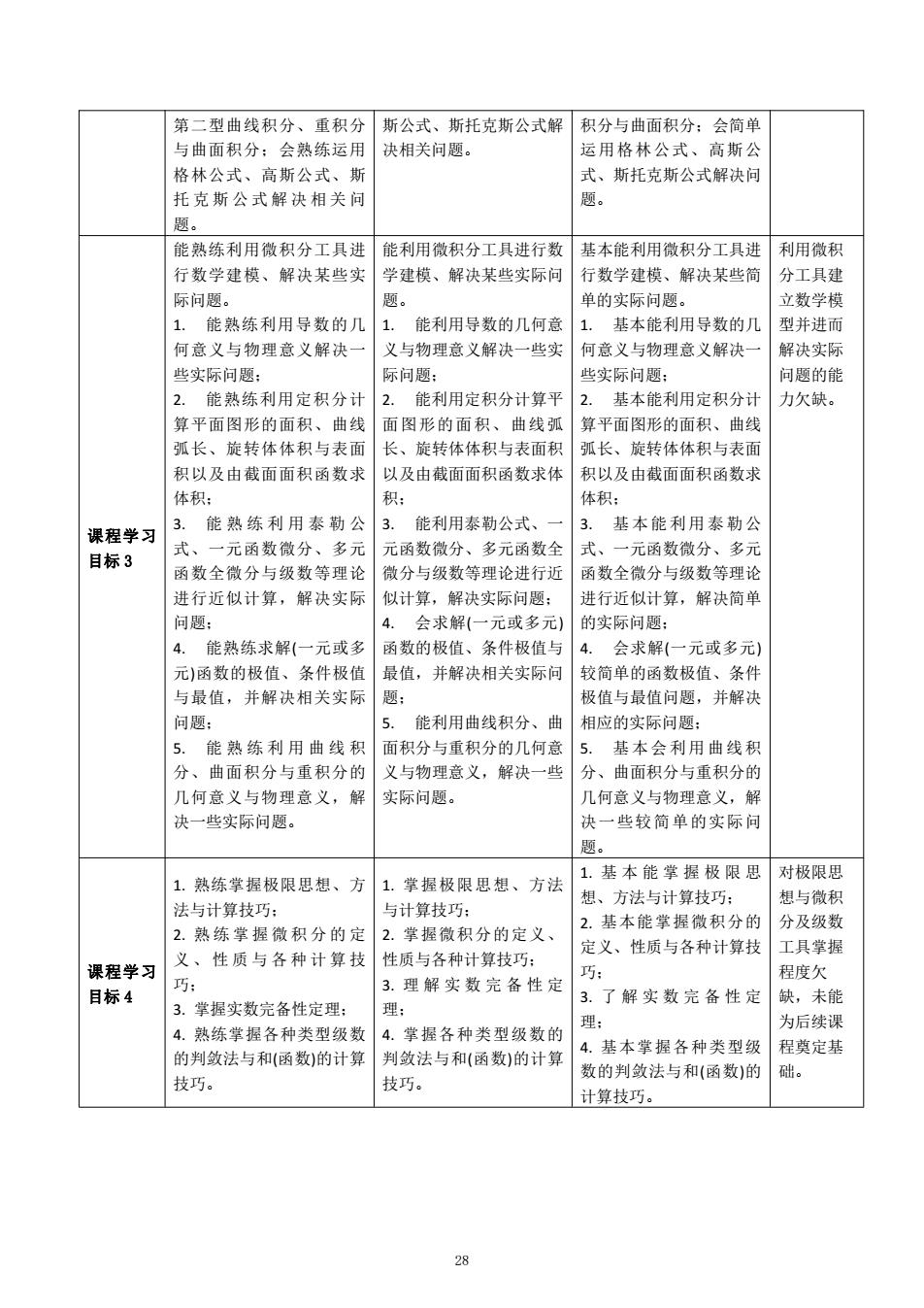
第二型曲线积分、重积分 斯公式、斯托克斯公式解 积分与曲面积分:会简单 与曲面积分:会熟练运用 决相关问题。 运用格林公式、高斯公 格林公式、高斯公式、斯 式、 斯托克斯公式解决问 托克斯公式解决相关问 题。 题。 能熟练利用微积分工具进 能利用微积分工具进行数 基本能利用微积分工具进 利用微积 行数学建模、解决某些实 学建模、解决某些实际问 行数学建模、解决某些简 分工具建 际问题。 题。 单的实际问题。 立数学模 1.能熟练利用导数的几 1. 能利用导数的几何意 1. 基本能利用导数的几 型并进而 何意义与物理意义解决一 义与物理意义解决一些实 何意义与物理意义解决一 解决实际 些实际问题: 际问题: 些实际问题: 问题的能 2. 能熟练利用定积分计 2. 能利用定积分计算平 2. 基本能利用定积分计 力欠缺。 算平面图形的面积、曲线 面图形的面积、曲线弧 算平面图形的面积、曲线 弧长、旋转体体积与表面 长、旋转体体积与表面积 弧长、旋转体体积与表面 积以及由截面面积函数求 以及由截面面积函数求体 积以及由截面面积函数求 体积: 积: 体积: 3. 能熟练利用泰勒公 3. 课程学习 能利用泰勒公式、一 3.基本能利用泰勒公 式、一元函数微分、多元 元函数微分、多元函数全 式、一元函数微分、多元 目标3 函数全微分与级数等理论 微分与级数等理论进行近 函数全微分与级数等理论 进行近似计算,解决实际 似计算,解决实际问题: 进行近似计算,解决简单 问题: 4.会求解(一元或多元) 的实际问题: 4. 能熟练求解(一元或多 函数的极值、条件极值与 4.会求解(一元或多元) 元)函数的极值、条件极值 最值,并解决相关实际问 较简单的函数极值、条件 与最值,并解决相关实际 题 极值与最值问题,并解决 问题: 5. 能利用曲线积分、曲 相应的实际问题: 5.能熟练利用曲线积 面积分与重积分的几何意 5. 基本会利用曲线积 分、曲面积分与重积分的 义与物理意义,解决一些 分、曲面积分与重积分的 几何意义与物理意义,解 实际问题。 几何意义与物理意义,解 决一些实际问题。 决一些较简单的实际问 题。 1.基本能掌握极限思 对极限思 1.熟练掌握极限思想、方 1.掌握极限思想、方法 法与计算技巧: 想、方法与计算技巧: 想与微积 与计算技巧: 2.基本能掌握微积分的 分及级数 2.熟练掌握微积分的定 2.掌握微积分的定义、 义、性质与各种计算技 定义、性质与各种计算技 工具掌握 性质与各种计算技巧: 课程学习 巧; 3.理解实数完备性定 巧: 程度欠 目标4 3.了解实数完备性定 缺,未能 3. 掌握实数完备性定理: 理: 理; 为后续课 4.熟练掌握各种类型级数 4.掌握各种类型级数的 4.基本掌握各种类型级 程奠定基 的判敛法与和(函数)的计算 判敛法与和(函数)的计算 数的判敛法与和(函数)的 础。 技巧。 技巧。 计算技巧。 28
第二型曲线积分、重积分 与曲面积分;会熟练运用 格林公式、高斯公式、斯 托 克 斯 公 式 解 决 相 关 问 题。 斯公式、斯托克斯公式解 决相关问题。 积分与曲面积分;会简单 运用格林公式、高斯公 式、斯托克斯公式解决问 题。 课程学习 目标 3 能熟练利用微积分工具进 行数学建模、解决某些实 际问题。 1. 能熟练利用导数的几 何意义与物理意义解决一 些实际问题; 2. 能熟练利用定积分计 算平面图形的面积、曲线 弧长、旋转体体积与表面 积以及由截面面积函数求 体积; 3. 能 熟 练 利 用 泰 勒 公 式、一元函数微分、多元 函数全微分与级数等理论 进行近似计算,解决实际 问题; 4. 能熟练求解(一元或多 元)函数的极值、条件极值 与最值,并解决相关实际 问题; 5. 能 熟 练 利 用 曲 线 积 分、曲面积分与重积分的 几何意义与物理意义,解 决一些实际问题。 能利用微积分工具进行数 学建模、解决某些实际问 题。 1. 能利用导数的几何意 义与物理意义解决一些实 际问题; 2. 能利用定积分计算平 面图形的面积、曲线弧 长、旋转体体积与表面积 以及由截面面积函数求体 积; 3. 能利用泰勒公式、一 元函数微分、多元函数全 微分与级数等理论进行近 似计算,解决实际问题; 4. 会求解(一元或多元) 函数的极值、条件极值与 最值,并解决相关实际问 题; 5. 能利用曲线积分、曲 面积分与重积分的几何意 义与物理意义,解决一些 实际问题。 基本能利用微积分工具进 行数学建模、解决某些简 单的实际问题。 1. 基本能利用导数的几 何意义与物理意义解决一 些实际问题; 2. 基本能利用定积分计 算平面图形的面积、曲线 弧长、旋转体体积与表面 积以及由截面面积函数求 体积; 3. 基 本能 利用 泰勒 公 式、一元函数微分、多元 函数全微分与级数等理论 进行近似计算,解决简单 的实际问题; 4. 会求解(一元或多元) 较简单的函数极值、条件 极值与最值问题,并解决 相应的实际问题; 5. 基 本会 利用 曲线 积 分、曲面积分与重积分的 几何意义与物理意义,解 决一些较简单的实际问 题。 利用微积 分工具建 立数学模 型并进而 解决实际 问题的能 力欠缺。 课程学习 目标 4 1. 熟练掌握极限思想、方 法与计算技巧; 2. 熟 练 掌 握 微 积 分 的 定 义 、 性 质 与 各 种 计 算 技 巧; 3. 掌握实数完备性定理; 4. 熟练掌握各种类型级数 的判敛法与和(函数)的计算 技巧。 1. 掌握极限思想、方法 与计算技巧; 2. 掌握微积分的定义、 性质与各种计算技巧; 3. 理 解 实 数 完 备 性 定 理; 4. 掌握各种类型级数的 判敛法与和(函数)的计算 技巧。 1. 基 本 能 掌 握 极 限 思 想、方法与计算技巧; 2. 基本能掌握微积分的 定义、性质与各种计算技 巧; 3. 了 解 实 数 完 备 性 定 理; 4. 基本掌握各种类型级 数的判敛法与和(函数)的 计算技巧。 对极限思 想与微积 分及级数 工具掌握 程度欠 缺,未能 为后续课 程奠定基 础。 28
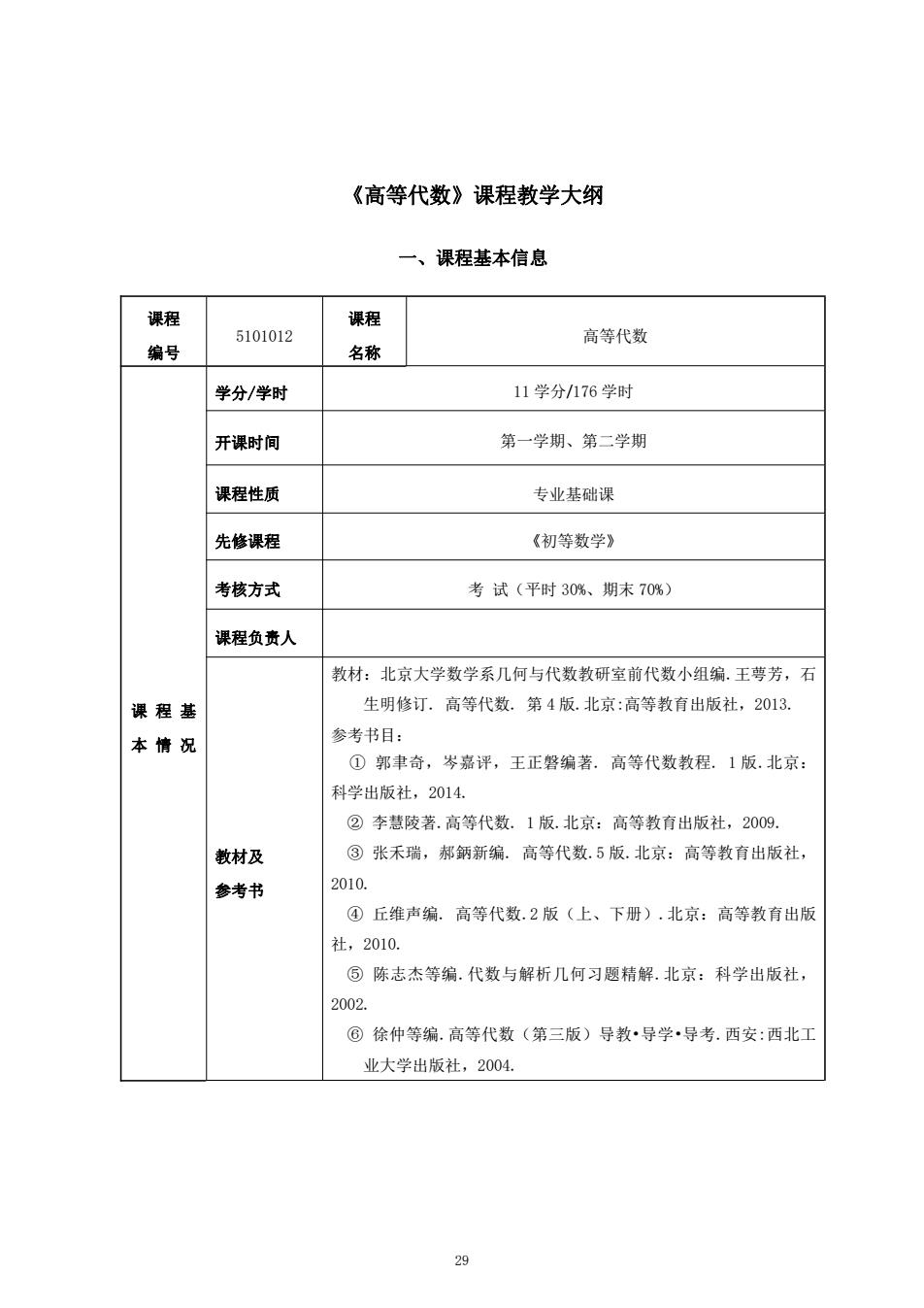
《高等代数》课程教学大纲 一、课程基本信息 课程 课程 5101012 高等代数 编号 名称 学分/学时 11学分/176学时 开课时间 第一学期、第二学期 课程性质 专业基础课 先修课程 《初等数学》 考核方式 考试(平时30%、期末70%) 课程负责人 教材:北京大学数学系几何与代数教研室前代数小组编.王萼芳,石 课程基 生明修订.高等代数.第4版.北京:高等教育出版社,2013. 本情况 参考书目: ①郭聿奇,岑嘉评,王正磐编著.高等代数教程.1版.北京: 科学出版社,2014. ②李慧陵著.高等代数.1版.北京:高等教育出版社,2009. 教材及 ③张禾瑞,郝鈵新编.高等代数.5版.北京:高等教育出版社, 参考书 2010. ④丘维声编.高等代数.2版(上、下册).北京:高等教育出版 社,2010. ⑤陈志杰等编.代数与解析几何习题精解.北京:科学出版社, 2002. ⑥徐仲等编.高等代数(第三版)导教·导学·导考.西安:西北工 业大学出版社,2004. 29
《高等代数》课程教学大纲 一、课程基本信息 课程 编号 5101012 课程 名称 高等代数 课 程 基 本 情 况 学分/学时 11 学分/176 学时 开课时间 第一学期、第二学期 课程性质 专业基础课 先修课程 《初等数学》 考核方式 考 试(平时 30%、期末 70%) 课程负责人 教材及 参考书 教材:北京大学数学系几何与代数教研室前代数小组编.王萼芳,石 生明修订. 高等代数. 第 4 版.北京:高等教育出版社,2013. 参考书目: ① 郭聿奇,岑嘉评,王正磐编著. 高等代数教程. 1 版.北京: 科学出版社,2014. ② 李慧陵著.高等代数. 1 版.北京:高等教育出版社,2009. ③ 张禾瑞,郝鈵新编. 高等代数.5 版.北京:高等教育出版社, 2010. ④ 丘维声编. 高等代数.2 版(上、下册).北京:高等教育出版 社,2010. ⑤ 陈志杰等编.代数与解析几何习题精解.北京:科学出版社, 2002. ⑥ 徐仲等编.高等代数(第三版)导教•导学•导考.西安:西北工 业大学出版社,2004. 29