
曲线的切向量 例4自z0经z1到z2折线段的参数方程 z(e)=o+t2-zo),0≤t≤1 z1+t(z2-z1),1≤t≤2 该曲线在t=1处通常不可导,故不是光滑曲线,但是逐段光滑的. 例5求圆周z(0)=z0+rei8,0e[0,2m]的切向量. 解先将方程写为实形式 x(0)=x0+rc0s0 求导数 (x'(0)=-rsine y(0)=yo +rsine Iy'(e)=rcose 将导数写回复形式z'(t)=-r(sin0-icos0)=irei8
曲线的切向量 例4 自 𝑧0 经 𝑧1 到 𝑧2 折线段的参数方程 𝑧 𝑡 = ൜ 𝑧0 + 𝑡 𝑧1 − 𝑧0 ,0 ≤ 𝑡 ≤ 1 𝑧1 + 𝑡(𝑧2 − 𝑧1),1 ≤ 𝑡 ≤ 2 该曲线在 𝑡 = 1 处通常不可导,故不是光滑曲线,但是逐段光滑的. 例5 求圆周 𝑧 𝜃 = 𝑧0 + 𝑟𝑒 𝑖𝜃 ,𝜃 ∈ 0,2𝜋 的切向量. 解 先将方程写为实形式 ൝ 𝑥 𝜃 = 𝑥0 + 𝑟 cos 𝜃 𝑦 𝜃 = 𝑦0 + 𝑟 sin 𝜃 求导数 ቊ 𝑥 ′ 𝜃 = −𝑟 sin 𝜃 𝑦′ 𝜃 = 𝑟 cos𝜃 将导数写回复形式 𝑧 ′ 𝑡 = −𝑟 sin 𝜃 − 𝑖 cos𝜃 = 𝑖𝑟𝑒 𝑖𝜃 .
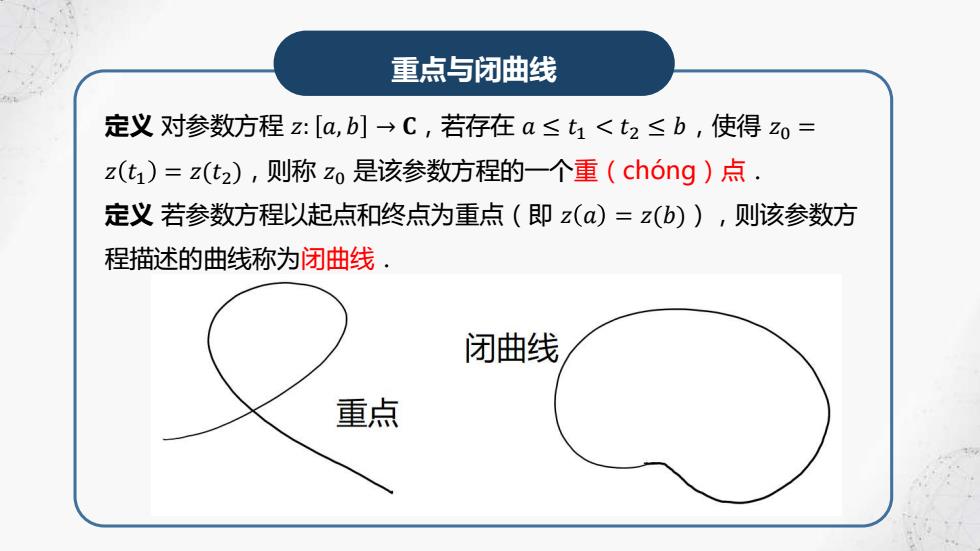
重点与闭曲线 定义对参数方程z:[a,b]→C,若存在a≤t1<t2≤b,使得z0= z(t1)=z(t2),则称z0是该参数方程的一个重(ch6ng)点. 定义若参数方程以起点和终点为重点(即z(a)=z(b)),则该参数方 程描述的曲线称为闭曲线, 闭曲线 重点
重点与闭曲线 定义 对参数方程 𝑧: 𝑎, 𝑏 → 𝐂,若存在 𝑎 ≤ 𝑡1 < 𝑡2 ≤ 𝑏,使得 𝑧0 = 𝑧 𝑡1 = 𝑧(𝑡2),则称 𝑧0 是该参数方程的一个重(chóng)点. 定义 若参数方程以起点和终点为重点(即 𝑧 𝑎 = 𝑧(𝑏)),则该参数方 程描述的曲线称为闭曲线.