
01 三角形式和指数形式 目录》 02 幂与根 CONTENTS 03 球极投影
01 三角形式和指数形式 目 录 CONTENTS 02 幂与根 03 球极投影

01 PART 三角形式与指数形式
三角形式与指数形式 01 PART
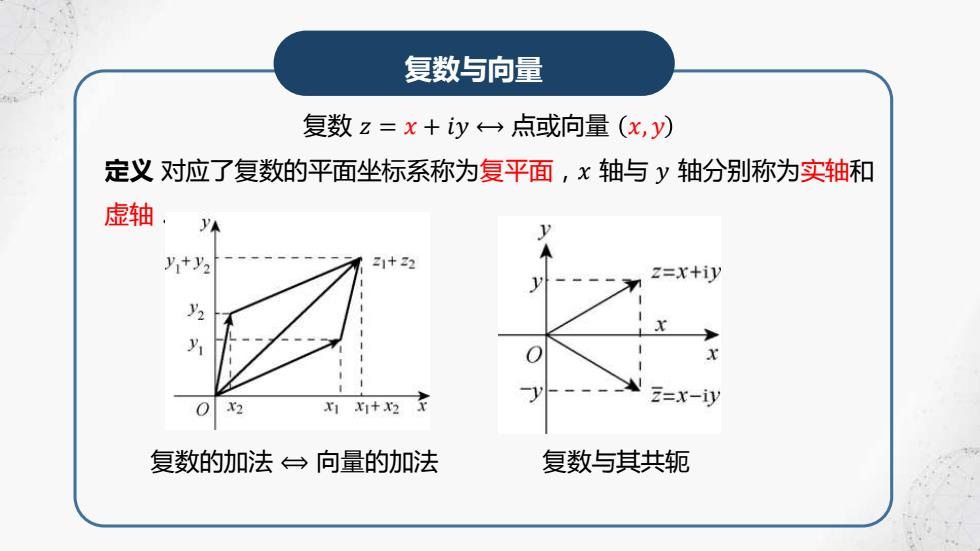
复数与向量 复数z=x+iy←→点或向量(x,y) 定义对应了复数的平面坐标系称为复平面,x轴与y轴分别称为实轴和 虚轴 1 +y2 21+22 z=x+iy X2 X1X+X2 z=x-iy 复数的加法台向量的加法 复数与其共轭
复数与向量 复数 𝑧 = 𝑥 + 𝑖𝑦 ⟷ 点或向量 𝑥, 𝑦 定义 对应了复数的平面坐标系称为复平面,𝑥 轴与 𝑦 轴分别称为实轴和 虚轴. 复数的加法 ⟺ 向量的加法 复数与其共轭
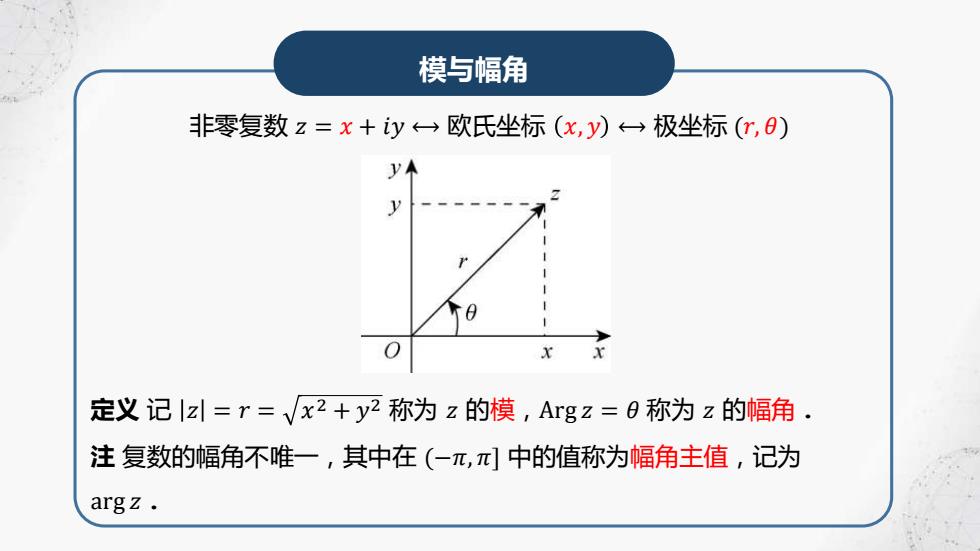
模与幅角 非零复数z=x+y←→欧氏坐标(x,y)←→极坐标(亿,) y 定义记|z=r=√x2+y2称为z的模,Argz=0称为z的幅角. 注复数的幅角不唯一,其中在(-兀,π]中的值称为幅角主值,记为 argz
模与幅角 非零复数 𝑧 = 𝑥 + 𝑖𝑦 ⟷ 欧氏坐标 𝑥, 𝑦 ⟷ 极坐标 (𝑟, 𝜃) 定义 记 𝑧 = 𝑟 = 𝑥 2 + 𝑦 2 称为 𝑧 的模,Arg 𝑧 = 𝜃 称为 𝑧 的幅角. 注 复数的幅角不唯一,其中在 (−𝜋, 𝜋] 中的值称为幅角主值,记为 arg 𝑧.

三角形式 定义对复数z,若其在复平面对应点的极坐标为(工,),则称表达式 z=r(cos0+isin0) 为该复数的三角形式· 定理若z1=h(cos01+isin01),z2=2(cos02+isin日2),则 z1z2=12(cos(01+02)+isin(01+02). 证明只需注意到 (cos01+isin01)(cos02 +isin02) =(cos01 cos02-sin 01 sin 02)+i(sin 01 cos02 +cos01 sin02) =cos(01+02)+isin(01+02) 即可
三角形式 定义 对复数 𝑧,若其在复平面对应点的极坐标为 𝑟, 𝜃 ,则称表达式 𝑧 = 𝑟(cos 𝜃 + 𝑖 sin 𝜃) 为该复数的三角形式. 定理 若 𝑧1 = 𝑟1(cos𝜃1 + 𝑖 sin 𝜃1),𝑧2 = 𝑟2(cos𝜃2 + 𝑖 sin 𝜃2),则 𝑧1𝑧2 = 𝑟1𝑟2(cos(𝜃1 + 𝜃2) + 𝑖 sin(𝜃1 + 𝜃2)). 证明 只需注意到 cos 𝜃1 + 𝑖 sin 𝜃1 cos𝜃2 + 𝑖 sin 𝜃2 = (cos𝜃1 cos𝜃2 − sin 𝜃1 sin 𝜃2) + 𝑖 (sin 𝜃1 cos𝜃2 + cos𝜃1 sin 𝜃2) = cos(𝜃1 + 𝜃2) + 𝑖 sin(𝜃1 + 𝜃2) 即可.