
(3)实现的种类 ① 严格正则传递函数(G(∞)=0,D=0),其实现为(A,B,C)。 ② 正则传递函数(G(∞)≠0,D≠0),其实现为(A,B,C,D)。 ③ 非正则传递函数(G(∞)=∞),也存在实现,其实现具有 如下形式 Ei(t)=Ax(t)+Bu(t) y(t)=Cx(t)+Du(t) (5-9) 式中E为奇异阵。这种形式的系统称为广义系统,或奇异 系统。(本书不予讨论,在专门文献中研究)
( ) ( ) ( ) ( ) ( ) ( ) t t t t t t y Cx Du Ex Ax Bu = + & = + 式中 为奇异阵。这种形式的系统称为广义系统,或奇异 系统。(本书不予讨论,在专门文献中研究) E ⑶ 实现的种类 ① 严格正则传递函数( , ),其实现为( )。 ③ 非正则传递函数( ),也存在实现,其实现具有 如下形式 ② 正则传递函数( , ),其实现为( )。 G(∞) ≠ 0 G(∞) = 0 D = 0 A,B,C D ≠ 0 A,B,C,D G(∞) = ∞ (5-9)
5.2.2最小实现的性质 如果将例(5一5)的传递函数阵写成 Gs)=[G(s)G2(s)] 先分别求出Gs)和Gs)的实现,G(s)的实现就是这两个实现 的直和。 G(s)= G2(s)= G(s)的实现是 x1=-X1+41 G2(s)的实现是 「2 1 [0 -3-+
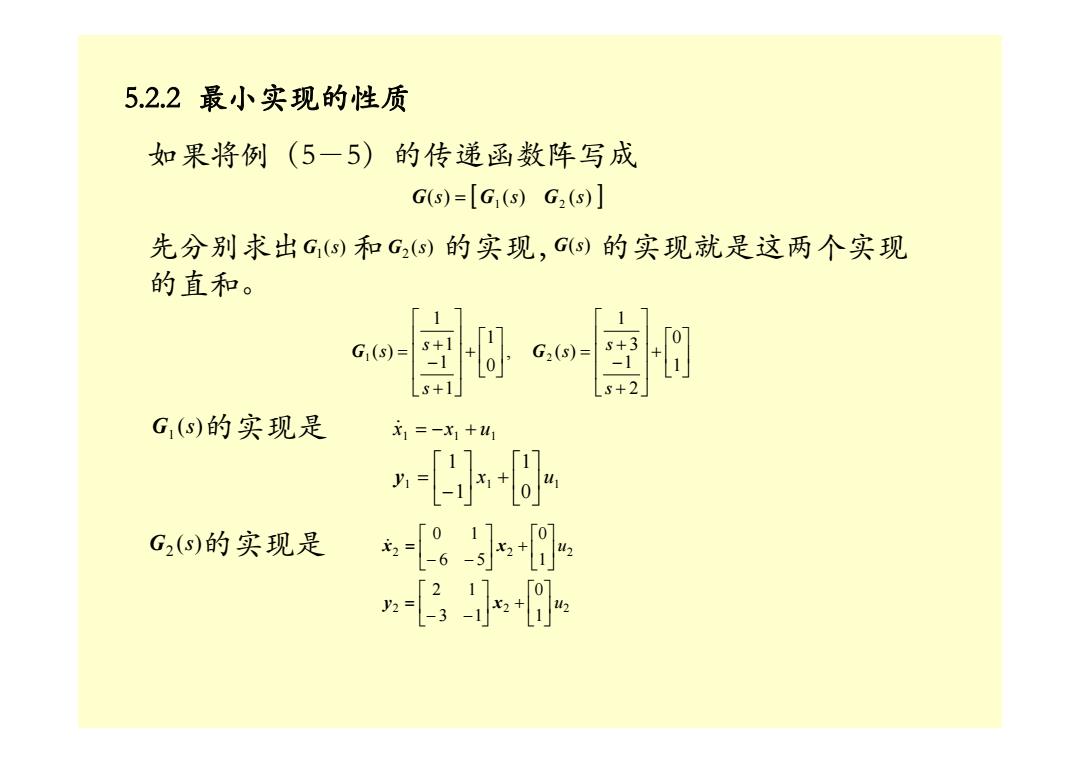
如果将例(5-5)的传递函数阵写成 G( ) [ G ( ) G ( ) ] 1 2 s = s s 先分别求出 和 的实现, 的实现就是这两个实现 的直和。 ( ) 1 G s ( ) 2 G s G(s) 5.2.2 最小实现的性质 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − + = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − + = 1 0 2 1 3 1 , ( ) 0 1 1 1 1 1 ( ) 1 2 s s s s s G s G G1 ( s )的实现是 1 1 1 1 1 1 0 1 1 1 x u x x u y ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ + ⎦ ⎤ ⎢ ⎣ ⎡ − = & = − + G 2 ( s )的实现是 2 2 2 2 2 2 1 0 3 1 2 1 1 0 6 5 0 1 u u y x x x ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ + ⎦ ⎤ ⎢ ⎣ ⎡ − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ + ⎦ ⎤ ⎢ ⎣ ⎡ − − & =

G(s)的实现是 -1 0 0 「10 = 0 0 1 x+0 41 0 0 -6 -5 0 1 12 这是一个3维(等于G(s)的维数)的实现。可以验证,它是 既能控又能观的。 可见,如果G(s)是可实现的,其实现不是唯一的,并且 实现的维数也可能是不同的。其中,维数最小的实现称为 最小实现
⎥⎦⎤ ⎢⎣⎡ ⎥⎦⎤ ⎢⎣⎡ ⎥ + ⎦⎤ ⎢⎣⎡− − − = ⎥⎦⎤ ⎢⎣⎡ ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ + ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ − − − = 2 1 2 1 1 1 1 0 1 3 1 1 2 1 0 1 0 0 1 0 0 6 5 0 0 1 1 0 0 u u u u y x x & x G(s) 的实现是 可见,如果 是可实现的,其实现不是唯一的,并且 实现的维数也可能是不同的。其中,维数最小的实现称为 最小实现。 G(s) 这是一个3维(等于 的维数)的实现。可以验证,它是 既能控又能观的。 G(s)

(1)定义 G(s)的实现中,维数最小的实现叫做G(s)的最小实现。 由于传递函数只描述系统中既能控又能观子系统的行为 ,如果G(s的某个实现不是既能控又能观的,那么其既能控 又能观的子系统也是G(s)的实现,在这个意义上,G(s)的最小 实现也称为不可简约的实现或既能控又能观的实现。 最小实现台既能控又能观的实现台不可简约的实现 (2)最小实现的性质 ① 定理5一2(4,B,CD)是G(s)最小实现的充分必要条件是: (4,B,CD)是既能控又能观的。 证明 必要性:如果(A,B,C,D)是G(s)的一个最小实现,则(A,B,C,D) 是既能控又能观的
⑴ 定义 G(s) 的实现中,维数最小的实现叫做 的最小实现 G(s) 。 由于传递函数只描述系统中既能控又能观子系统的行为 ,如果 的某个实现不是既能控又能观的,那么其既能控 又能观的子系统也是 的实现,在这个意义上, 的最小 实现也称为不可简约的实现或既能控又能观的实现。 G(s) G(s) G(s) 最小实现 既能控又能观的实现 不可简约的实现 ⇔ ⇔ ⑵ 最小实现的性质 ① 定理5-2 是 最小实现的充分必要条件是: 是既能控又能观的。 (A,B,C, D) (A,B,C, D) G(s) 证明 必要性:如果 是 的一个最小实现,则 是既能控又能观的。 (A,B,C, D) (A,B,C, D) G(s)

反证法:如果(A,B,C,D)是Gs)的一个最小实现,而又不是既 能控又能观的,则可以通过结构分解得到一个既能控又能 观的子系统,它的维数小于(A,B,C,D)的维数,而又具有相同 的传递函数阵,说明(4,B,C,D)不是的最小实现,与假设矛 盾。 充分性:如果(A,B,C,D是既能控的又能观的,则它一定是G(s) 的一个最小实现。 反证法:如果(4,B,CD)是n维的,且是既能控的又能观的,而 又不是Gs最小实现,则必存在一个n<n维的最小实现(A,B,C,D) ,它与(4,B,CD)具有相同的传递函数阵G(s)=G(s),即 C(sI-A)-B+D=C(sI-A)-B+D
反证法:如果 是 的一个最小实现,而又不是既 能控又能观的,则可以通过结构分解得到一个既能控又能 观的子系统,它的维数小于 的维数,而又具有相同 的传递函数阵,说明 不是的最小实现,与假设矛 盾。 (A,B,C, D) G(s) (A,B,C, D) (A,B,C, D) 充分性:如果 是既能控的又能观的,则它一定是 的一个最小实现。 (A,B,C, D ) G(s) 反证法:如果 是 维的,且是既能控的又能观的,而 又不是 最小实现,则必存在一个 维的最小实现 ,它与 具有相同的传递函数阵 ,即 (A,B,C, D) n G(s) n < n (A,B,C, D) (A,B,C, D) G (s) = G(s) C I − A B + D = C I − A B + D −1 −1 ( s ) ( s ) r