
(2)G(s)可实现为(A,B,C,D)的条件 定理5一1G(s)可实现的充分必要条件是:G(s)是正则(或严 格正则)有理函数阵。 证明 必要性:若(A,B,C,D)是G(s)的一个实现,则有 G(s)=C(sI-A)-B+D C[adj(sI-A)1B+D det(sI-A) 若D≠0,G(s)是正则有理函数阵。若D=0,G(S)是严格正则有理 函数阵。所以如果可实现,则G(s)必定是正则有理(或严格 正则)函数阵。 充分性:若G()是正则有理函数,则存在一个实现(4,B,C,D), 满足 G(s)=C(sI-A)B+D
⑵ 可实现为 的条件 G ( s ) 定理5-1 可实现的充分必要条件是: 是正则(或严 格正则)有理函数阵。 G ( s ) G ( s ) 证明 必要性:若 是 的一个实现,则有 (A,B,C, D ) G ( s ) G = C I − A B + D −1 (s) (s ) C I A B D I A − + − = [ ( )] det( ) 1 adj s s 若 , 是正则有理函数阵。若 , 是严格正则有理 函数阵。所以如果可实现,则 必定是正则有理(或严格 正则)函数阵。 D ≠ 0 G ( s ) D = 0 G ( s ) G ( s ) 充分性: 若 是正则有理函数,则存在一个实现 , 满足 G ( s ) G = C I − A B + D −1 (s) (s ) (A,B,C, D ) (A,B,C, D )
设G(s)是9×p有理函数阵,可写成 G(s)=Gm(s)+G(∞) (5-5) 式中,G(∞)是G(s)中的常数阵部分 Gps是Gs)的严格正则部分,可写成 69-08O Ng=N,s+N,s++N5+N,】 (5-6) 式中,N与N,都是9×P有理函数阵 d(s)是G(s)中所有子式的首一最小公(倍)分母 d(s)=s'+a1s-+…+a,-1s+a, (5-7) 可以证明以下方程(A,B,C,D)就是G(s)的一个实现 0 Ip 0… 0 0 0 文= 0 x+ 0 0 Ip 0 (5-8) -aIp-a-lp… … y= N N:x+G(co)u
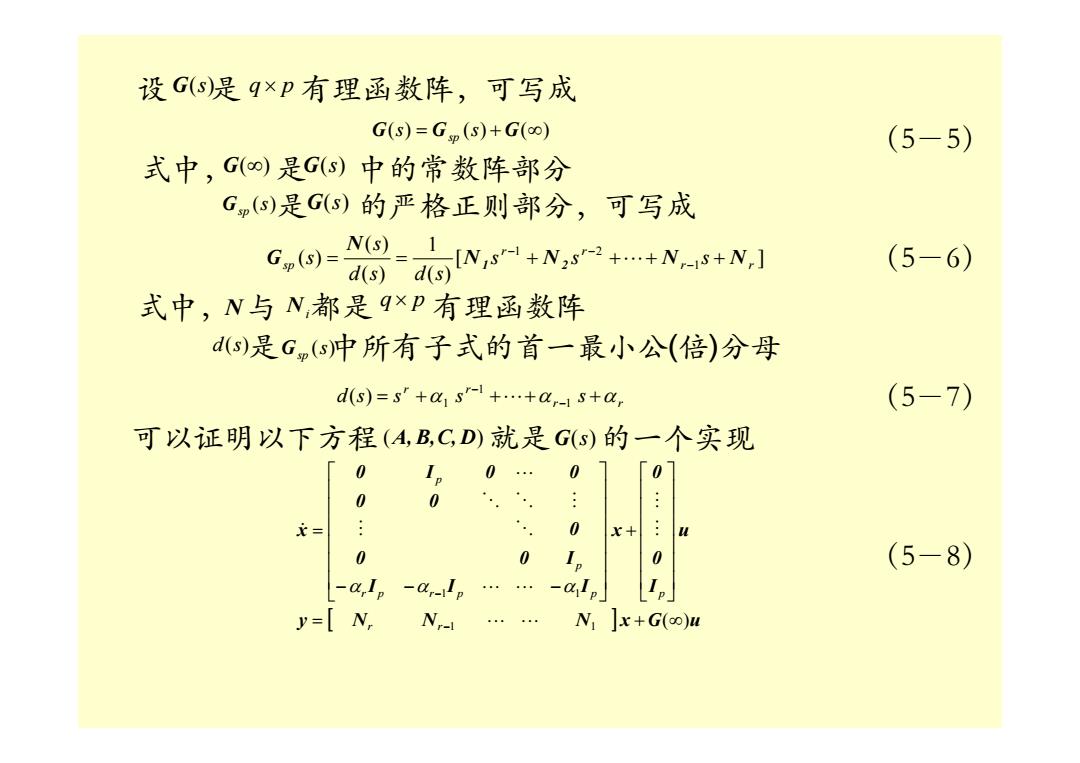
设 是 有理函数阵,可写成 G ( s ) q × p G(s) = G (s) + G(∞) sp 式中, 是 中的常数阵部分 是 的严格正则部分,可写成 G ( ∞ ) (s) Gsp G ( s ) G ( s ) [ ] ( ) 1 ( ) ( ) ( ) 1 1 2 r r r r sp s s s d s d s s s N N N N N G = = 1 + 2 + + − + − − L (5-5) (5-6) 式中, 与 都是 有理函数阵 d(s) (s) Gsp N Ni q × p r r r r d s = s + α s + + α − s + α − 1 1 1 ( ) L 是 中所有子式的首一最小公 ( 倍 )分母 可以证明以下方程 就是 的一个实现 (A,B,C, D ) G ( s ) y [ ] N N N x G u u I 0 0 x I I I 0 0 I 0 0 0 0 I 0 0 x ( ) 1 1 1 1 = + ∞ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = − − L L M M L L M O O O M L & r r r p r p p p p p α α α (5-7) (5-8)

式中,I,与0是p×p单位阵与零阵 A是pxp阵,它由P列r行p×p阵组成 B是PxP阵,它由r列P×P阵组成 C是9×p阵,它由”行q×p阵组成 D=G(co) (证略) 式(⑤一8)的实现称为的能控性实现。它也可实现为能观性实 现。对多变量系统,按此法求得的实现一般不是最小实现
式中, 与 是 单位阵与零阵 是 阵,它由 列 行 阵组成 是 阵,它由 列 阵组成 是 阵,它由 行 阵组成 (证略) p I 0 p × p A rp × rp r B rp × p C q × rp r q × p p × p r p × p r D = G ( ∞ ) 式(5-8)的实现称为的能控性实现。它也可实现为能观性实 现。对多变量系统,按此法求得的实现一般不是最小实现

例5一5求下列G(s)的实现 S+2 1 G(s)= S+1 S+3 s+1 s+i s+2 G(s)是正则双输入双输出系统。现将它分解为 G(s)=Gm(s)+G(∞) 1 1 s+1 S+3 T10 0 +2 G知(s)所有子式的首一最小公分母 d(s)=(s+1)(s+2)(s+3)=s3+6s2+11s+6 G(s)=N(s)_1 Ns+N2s-2++N-1s+N,] d(s)d(s) o+we+[%3
例5-5 求下列 的实现 G(s) ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ ++ ++ + + = 21 1 3 1 12 ( ) ss s s s s s G s G(s)是正则双输入双输出系统。现将它分解为 ⎥⎦⎤ ⎢⎣⎡ +⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ +− +−+ + = = + ∞ 0 1 1 0 2 1 1 1 3 1 1 1 ( ) ( ) ( ) s s s s s s G Gsp G Gsp (s)所有子式的首一最小公分母 ( ) ( 1)( 2)( 3) 6 11 6 3 2 d s = s + s + s + = s + s + s + ⎟⎟⎠⎞ ⎜⎜⎝⎛ ⎥⎦⎤ ⎢⎣⎡− − + ⎥⎦⎤ ⎢⎣⎡− − + ⎥⎦⎤ ⎢⎣⎡ + + + − − = = = + + + − + − − 6 3 6 2 5 3 5 4 1 1 1 1 ( 1)( 2)( 3) 1 [ ] ( ) 1 ( ) ( ) ( ) 2 1 1 2 s s s s s s s s d s d s s s r r r r sp N N N N N G 1 2 L

可得 1=6,a2=11,a3+6 x-[小[[ G(s)的实现是 00 1 0 0 0 To 01 00 0 1 0 0 0 0 00 0 0 1 0 0 文= 0 0 0 X+ 0 0 1 0 0 -6 0 -11 0 -6 0 1 0 0 -6 -110 -6 01 6 2 [1 0 y= -6 -3-5-3 x+ G)是2×2矩阵,是3阶的,而上述实现是6维的。它不是最小 实现
α 1 = 6 , α 2 = 11, α 3 + 6 ⎥⎦⎤ ⎢⎣⎡− − ⎥ = ⎦⎤ ⎢⎣⎡− − ⎥ = ⎦⎤ ⎢⎣⎡− − = 6 3 6 2 5 3 5 4 1 1 1 1 1 2 N 3 N , N , y x u x x u ⎥⎦⎤ ⎢⎣⎡ ⎥ + ⎦⎤ ⎢⎣⎡− − − − − − = ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡ + ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡ − − − − − − = 0 1 1 0 6 3 5 3 1 1 6 2 5 4 1 1 0 1 1 0 0 0 0 0 0 0 0 0 0 6 0 11 0 6 6 0 11 0 6 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 & 可得 G(s)的实现是 是 矩阵,是 阶的,而上述实现是6维的。它不是最小 实现。 G(s) 2×2 3