
类似地,设函数f(x)在区间[a,b)上连续,而在 点b的左邻域内无界,取ε>0 如果极限m心fxd存在,则定义 +0。 fs=m达 (5) 否则,就称广义积分心f(x)dk发散 前页 返回
前页 后页 返回 类似地, 设函数 f (x)在区间[a, b)上连续, 而在 点 b 的左邻域内无界, 取 > 0. b a lim f (x)dx 0 如果极限 存在,则定义 b a b a f (x)dx lim f (x)dx 0 (5) 否则, 就称广义积分 发散. b a f (x)dx

设函数fx)在区间[a,b]上除点c(a<c<b) 外连续,而在点c的邻域内无界,如果两个广义 积分 Cfx)d与心fx) 都收敛,则定义 (ds=ds+ limdsm()ds (6) 否则,就称广义积分心fx)d发散 前页 后页 返回
前页 后页 返回 设函数 f (x)在区间[a, b]上除点c (a < c < b) 外连续, 而在点 c 的邻域内无界, 如果两个广义 积分 b c c a f (x)dx与 f (x)dx 都收敛, 则定义 b c c a b a f (x)dx f (x)dx f (x)dx b c c a f x dx f x dx lim ( ) lim ( ) 0 0 (6) 否则, 就称广义积分 发散. b a f (x)dx
例6计g广义积分。本 (a>0) 解:因为lim xa-0va-x2 =+00 所以,x=a为被积函数的无穷 间断点 于是八m dx 1 a 0 a-sax 图5-7-1 -lin,arosin -aresin 8→+0 后页 返回
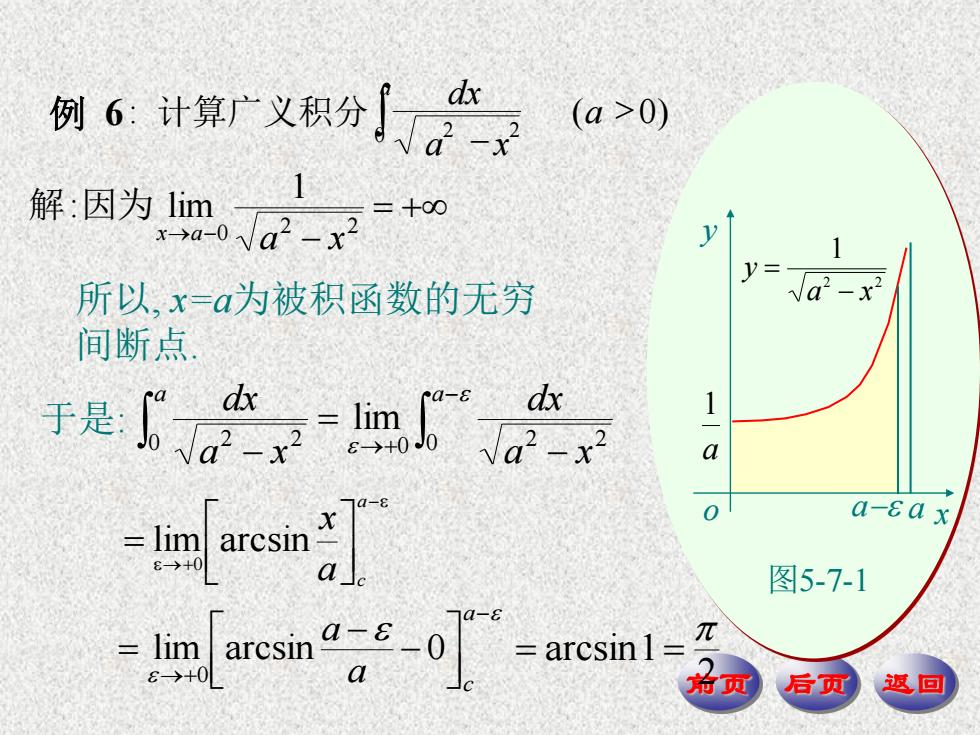
前页 后页 返回 2 2 0 1 : lim a x x a 解 因为 所以, x=a为被积函数的无穷 间断点. 于是: a a a x dx a x dx 0 2 2 0 0 2 2 lim a a c x lim arcsin 0 a c a a lim arcsin 0 0 2 arcsin1 o y a a x a 1 2 2 1 a x y 图5-7-1 ) a x dx a 6: ( 0 0 2 2 例 计算广义积分 a

例7 计算广义积分 dx 解 d (x-1)3 =+v dx x (x-1) =m。 (x-)=3 )-==32 x dx …心 x-0=3(1+/2). dx 前页 后页 返回
前页 后页 返回 解 2 3 3 0 ( 1) dx x 1 0 3 1 3 2 ( 1) ( ) x dx 1 0 3 2 (x 1) dx 1 0 0 3 2 ( 1) lim x dx 3 3 1 3 2 (x 1) dx 3 0 1 3 2 ( 1) lim x dx 3 2, 3 3 0 3 2 (x 1) dx 3(1 2). 3 例7 计算广义积分 。 2 3 3 0 ( 1) dx x

例8证明 I=了u+心1+么与a无关并求英位 正1=了+1+ -+j4+a+4=-4 ,=a+e+(令x= 前页 后页 返回
前页 后页 返回 0 2 (1 )(1 ) 1 dx与无关并求其值 x x I 例8 证明 证 dx x x I 0 2 (1 )(1 ) 1 dx x x 1 0 1 2 (1 )(1 ) 1 1 2 I I dx x x I 1 0 1 2 (1 )(1 ) 1 ) 1 ( t 令x