
例9.2斜体字的生成 ·数据矩阵x 0.500.506.006.005.50 5.50 0 0 6.4208.008.00 1.588.00 表示英文大写空心字母N的各个节点 (1)用plot语句在子图1中画出其形状: (2)取A= 10.25 1 作为变换矩阵对x进行变 换,并在子图2中画出其图形; 画图的要点是要在给定的数据右方,补上第 一点的坐标,使画出的图形封闭
例9.2 斜体字的生成 • 数据矩阵 表示英文大写空心字母N的各个节点 (1)用plot语句在子图1中画出其形状; (2)取 作为变换矩阵对x进行变 换,并在子图2中画出其图形; 画图的要点是要在给定的数据右方,补上第 一点的坐标,使画出的图形封闭。 0 0.50 0.50 6.00 6.00 5.50 5.50 0 0 0 6.42 0 8.00 8.00 1.58 8.00 x = 1 0.25 0 1 A =
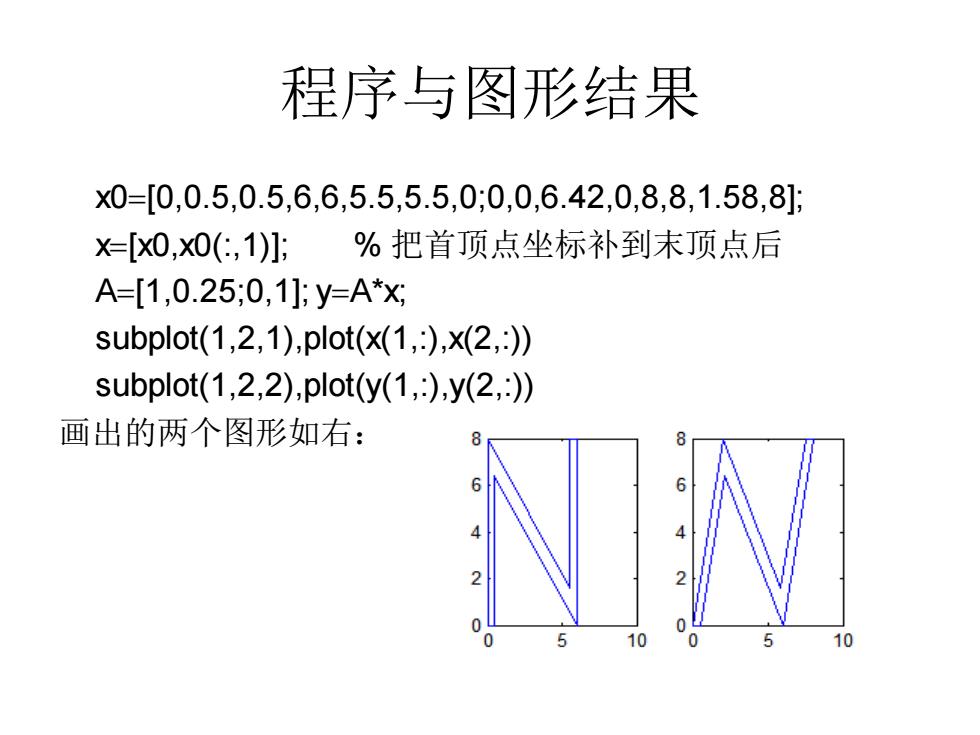
程序与图形结果 x0=[0,0.5,0.5,6,6,5.5,5.5,0;0,0,6.42,0,8,8,1.58,8 X=[x0,Xx0(:,1)]: %把首顶点坐标补到末顶点后 A=[1,0.25;0,1];y=A*X subplot(1,2,1),plot(x(1,:),x(2,) subplot(1,2,2),plot(y(1,),y(2,)) 画出的两个图形如右: 8 6 6 0 0 70
程序与图形结果 x0=[0,0.5,0.5,6,6,5.5,5.5,0;0,0,6.42,0,8,8,1.58,8]; x=[x0,x0(:,1)]; % 把首顶点坐标补到末顶点后 A=[1,0.25;0,1]; y=A*x; subplot(1,2,1),plot(x(1,:),x(2,:)) subplot(1,2,2),plot(y(1,:),y(2,:)) 画出的两个图形如右:

平移运动不能用二维变换实现 刚体在平面上的运动要用两个平移和一个转动来 描述,转动可以从上面的线性变换A5得到,但平 移y=X+C却不是一个线性变换。因为: ,(1)设ya=a+c;yb=b+c;则它们的和为 y=ya+yb=xa+xb+2C*x+C, 可见,它对加法不封闭; ·(2)设ya=xa+c;将它乘以常数k, y=kya=k(xa+c)=kxa+kC*kxa+C-x+C, 可见,它对乘法也不封闭;就是说,,这不符合线性 变换的规则,和y不属于同一个向量空间,无法 用矩阵乘法来实现平移变换y=X+C
平移运动不能用二维变换实现 • 刚体在平面上的运动要用两个平移和一个转动来 描述,转动可以从上面的线性变换A5得到,但平 移y=x+c却不是一个线性变换。因为: • (1)设ya=xa+c;yb=xb+c;则它们的和为 y=ya+yb=xa+xb+2c≠x+c, 可见,它对加法不封闭; • (2)设ya=xa+c;将它乘以常数k, y=kya=k(xa+c)=kxa+kc≠kxa+c=x+c, 可见,它对乘法也不封闭;就是说,这不符合线性 变换的规则,x和y 不属于同一个向量空间,无法 用矩阵乘法来实现平移变换y=x+c

平面运动模型的齐次坐标系 ·把平面问题映射到高维的空间来建立方程,有可 能把x和y由扩展了的向量空间来覆盖。把原来通 过原点的平面沿垂直方向提高一个单位,与原平 面保持平行,于是原来的x就用三维向量来表示为: X= X2 1 ·这样的坐标系称为齐次坐标系
平面运动模型的齐次坐标系 • 把平面问题映射到高维的空间来建立方程,有可 能把x和y由扩展了的向量空间来覆盖。把原来通 过原点的平面沿垂直方向提高一个单位,与原平 面保持平行,于是原来的x就用三维向量来表示为: • 这样的坐标系称为齐次坐标系。 1 2 1 x x x =

刚体平面运动用线性变换描述 ·此时可以把平移矩阵写成: 0 M= C2 0 ·因而平移运动y就可用X经线性变换实现了。 X1+C1 y=M·x= X2+C2 1 ·这个方法在研究刚体平面运动时非常有用
刚体平面运动用线性变换描述 • 此时可以把平移矩阵写成: • 因而平移运动y就可用x经线性变换实现了。 • 这个方法在研究刚体平面运动时非常有用。 1 2 1 0 0 1 0 0 1 c M c = 1 1 2 2 x +c x +c 1 y M x = =