
关于欧拉图的等价命题 口设G是非平凡连通图,以下三个命题等价: (1)G是欧拉图。 (2)G中每个顶点的度数均为偶数。 (3)G中所有的边包含在相互没有公共边的简单回路中
关于欧拉图的等价命题 设G是非平凡连通图,以下三个命题等价: (1) G是欧拉图。 (2) G中每个顶点的度数均为偶数。 (3) G中所有的边包含在相互没有公共边的简单回路中

半欧拉图的判定 口设G是连通图,G是半欧拉图当且仅当G恰有两个奇度点。 口证明: →设P是G中的欧拉通路(非回路),设P的始点与终点分别 是u,y,则对G中任何一点x,若x非u,V,则x的度数等于在P 中出现次数的2倍,而u,的度数则是它们分别在P中间位 置出现的次数的两倍再加1。 仁设G中两个奇度顶点是u,y,则G+uv是欧拉图,设欧拉回 路是C,则C中含uv边,∴.C-uv是G中的欧拉通路。(这表 明:如果试图一笔画出一个半欧拉图,必须以两个奇度 顶点为始点和终点。)
半欧拉图的判定 设G是连通图,G是半欧拉图 当且仅当 G恰有两个奇度点。 证明: 设P是G中的欧拉通路(非回路),设P的始点与终点分别 是u,v, 则对G中任何一点x, 若x非u,v,则x的度数等于在P 中出现次数的2倍,而u,v的度数则是它们分别在P中间位 置出现的次数的两倍再加1。 设G中两个奇度顶点是u,v, 则G+uv是欧拉图,设欧拉回 路是C, 则C中含uv边,C-uv是G中的欧拉通路。(这表 明:如果试图一笔画出一个半欧拉图,必须以两个奇度 顶点为始点和终点。)
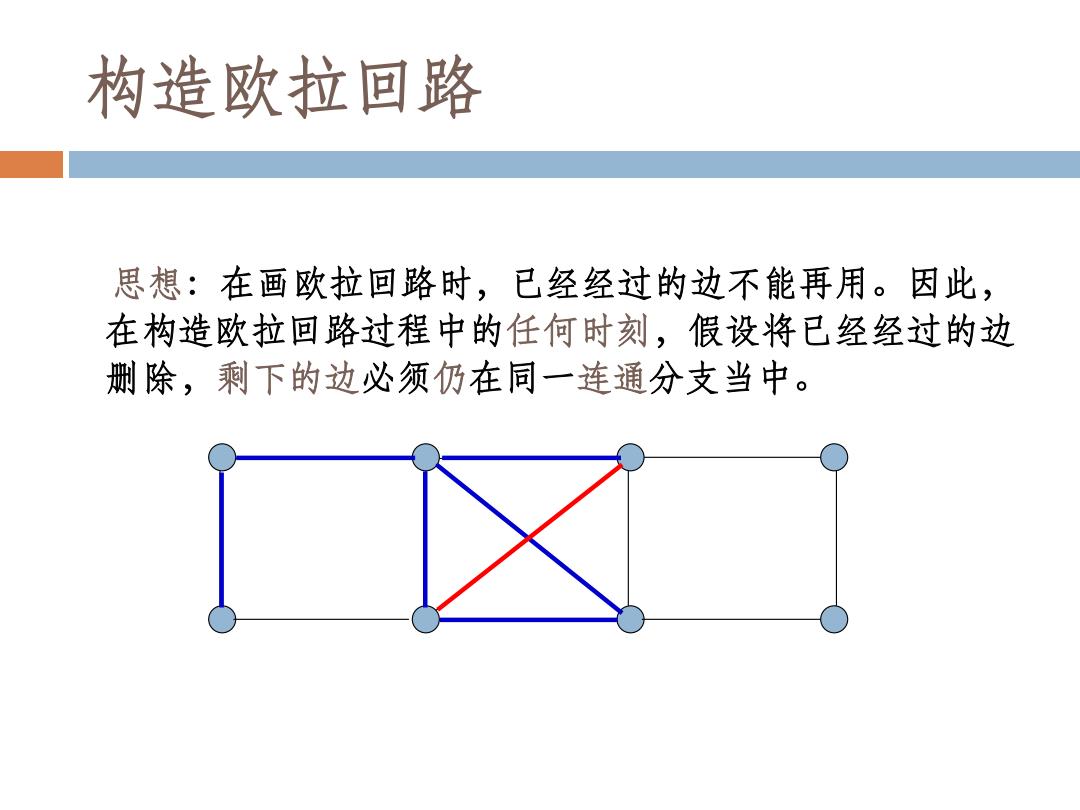
构造欧拉回路 思想:在画欧拉回路时,已经经过的边不能再用。因此, 在构造欧拉回路过程中的任何时刻,假设将已经经过的边 删除,剩下的边必须仍在同一连通分支当中
构造欧拉回路 思想:在画欧拉回路时,已经经过的边不能再用。因此, 在构造欧拉回路过程中的任何时刻,假设将已经经过的边 删除,剩下的边必须仍在同一连通分支当中

构造欧拉回路-Fleuty算法 口算法: 口输入:欧拉图G 口输出:简单通路P=VeVe2,…,eY+1,…,emVm,其中包含了 Ec中所有的元素。 1.任取vo∈Vc,令P。=vo 2.设?=veV1e2,…,eY,按下列原则从EG{e1,e2,…,e}中选择e+1o (a)e+1与v相关联; (b)除非别无选择,否则e+1不应是G-{e,e2,,e}中的割边。 3.反复执行第2步,直到无法执行时终止
构造欧拉回路-Fleury算法 算法: 输入:欧拉图G 输出:简单通路P = v0 e1 v1 e2 ,…,ei vi ei+1 ,…,em vm , 其中包含了 EG中所有的元素。 1. 任取v0VG ,令P0=v0 ; 2. 设Pi=v0 e1 v1 e2 ,…,ei vi , 按下列原则从EG -{e1 ,e2 ,…,ei }中选择ei+1。 (a) ei+1与vi相关联; (b) 除非别无选择,否则ei+1不应是G-{e1 ,e2 ,…,ei }中的割边。 3. 反复执行第2步,直到无法执行时终止

Fleuty算法的证明 口算法的终止性显然。 o 设算法终止时,Pm=voe1V1e2,…,eVe+1,…,CmVm 口其中诸e互异是显然的。只须证明: (1)Pm是回路,即vo=vm。 (2)Pm包括了G中所有的边。 令G=G-{e1e2,…,e} (I)(证明是回路)假设vom。由算法终止条件,在Gm中已没 有边与m相关联。假设除最后一次外,ⅴm在Pn中出现次, 则ⅴ的度数是2k+1,与G中顶点度数是偶数矛盾
Fleury算法的证明 算法的终止性显然。 设算法终止时,Pm = v0 e1v1 e2 ,…,eivi ei+1,…,emvm, 其中诸ei互异是显然的。只须证明: (1) P m是回路,即v0 =vm。 (2) P m包括了G中所有的边。 令Gi=G-{e1 ,e2 ,…,ei } (1) (证明是回路)假设v0 vm。由算法终止条件,在Gm中已没 有边与vm相关联。假设除最后一次外,vm在Pm中出现k次, 则vm的度数是2k+1, 与G中顶点度数是偶数矛盾