
1 概率化方法
概率化方法 1

概率化方法(Probabilistic Method) 2 WILEY 口一种用概率证明存在性的方法。 口先驱者:Paul Erd6s THE PROBABILISTIC METHOD Third Edition Noga Alon Joel H.Spencer WWw. wiley-laterscleace Series in Discrete Hathemutics an Optimization
概率化方法(Probabilistic Method) 一种用概率证明存在性的方法。 先驱者:Paul Erdős 2
概率化方法(Probabilistic Method) 3 口从盒子中随机选一个球 P(该球是蓝色的)>0 →盒中有蓝球 概率化方法: 定义一样本空间2及性质P:2→{0,1}: P(P=1)>0→x∈2.P(x)=1
概率化方法(Probabilistic Method) 从盒子中随机选一个球 𝑷 该球是蓝色的 > 𝟎 ⇒ 盒中有蓝球 3 概率化方法: 定义一样本空间𝛀及性质𝓟: 𝛀 → {𝟎, 𝟏}: 𝑷 𝓟 = 𝟏 > 𝟎 ⇒ ∃𝒙 ∈ 𝛀.𝓟(𝒙) = 𝟏
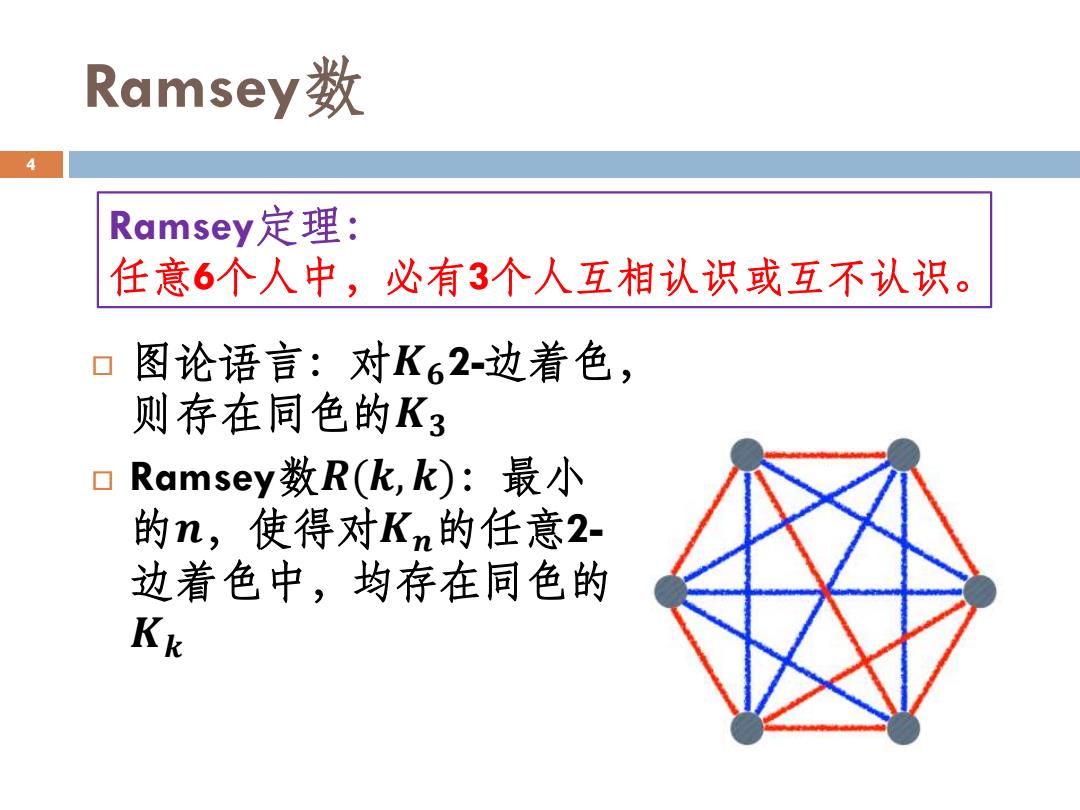
Ramsey数 4 Ramsey定理: 任意6个人中,必有3个人互相认识或互不认识。 图论语言:对K62-边着色, 则存在同色的K3 0 Ramsey数R(k,k):最小 的n,使得对Kn的任意2- 边着色中,均存在同色的 Kk
Ramsey数 图论语言:对𝑲𝟔2-边着色, 则存在同色的𝑲𝟑 Ramsey数𝑹(𝒌, 𝒌):最小 的𝒏,使得对𝑲𝒏的任意2- 边着色中,均存在同色的 𝑲𝒌 4 Ramsey定理: 任意6个人中,必有3个人互相认识或互不认识

R(k,)的一个下界 5 定理(Erd6s1947) 如果()21-(⑤)<1,则存在对Kn的某种2边着色,其不 含同色的Kk子图。 证:对每一条边e∈Kn独立随机着色,即以1/2的概率 着红色,1/2的概率着蓝色。 给定一Kk子图, P(该Kk同色)=21-() →P(存在间色Kk子图)≤(W)21-(台<1(Union bound) →P(不存在同色Kk子图)>0, →从而存在对Kn的某种2-边着色,其不含同色的Kk子图 推论:对所有k≥3,R(k,k)>l2k/2」
𝑹(𝒌, 𝒌)的一个下界 证:对每一条边𝒆 ∈ 𝑲𝒏独立随机着色,即以1/2的概率 着红色,1/2的概率着蓝色。 给定一𝑲𝒌子图, 𝑷 该𝑲𝒌同色 = 𝟐 𝟏− 𝒌 𝟐 ⟹ 𝑷 存在同色𝑲𝒌子图 ≤ 𝒏 𝒌 𝟐 𝟏− 𝒌 𝟐 < 𝟏 (Union bound) ⟹ 𝑷 不存在同色𝑲𝒌子图 > 𝟎, ⟹从而存在对𝑲𝒏的某种2-边着色,其不含同色的𝑲𝒌子图 5 定理(Erdős 1947) 如果 𝒏 𝒌 𝟐 𝟏− 𝒌 𝟐 < 𝟏,则存在对𝑲𝒏的某种2-边着色,其不 含同色的𝑲𝒌子图。 推论:对所有𝒌 ≥ 𝟑,𝑹 𝒌,𝒌 > ⌊𝟐 𝒌/𝟐 ⌋