系统分析: 建立表征系统的数学方程式并 求其解答 系统的描述 系统的求解
系统分析: 建立表征系统的数学方程式并 求其解答 系统的描述 系统的求解
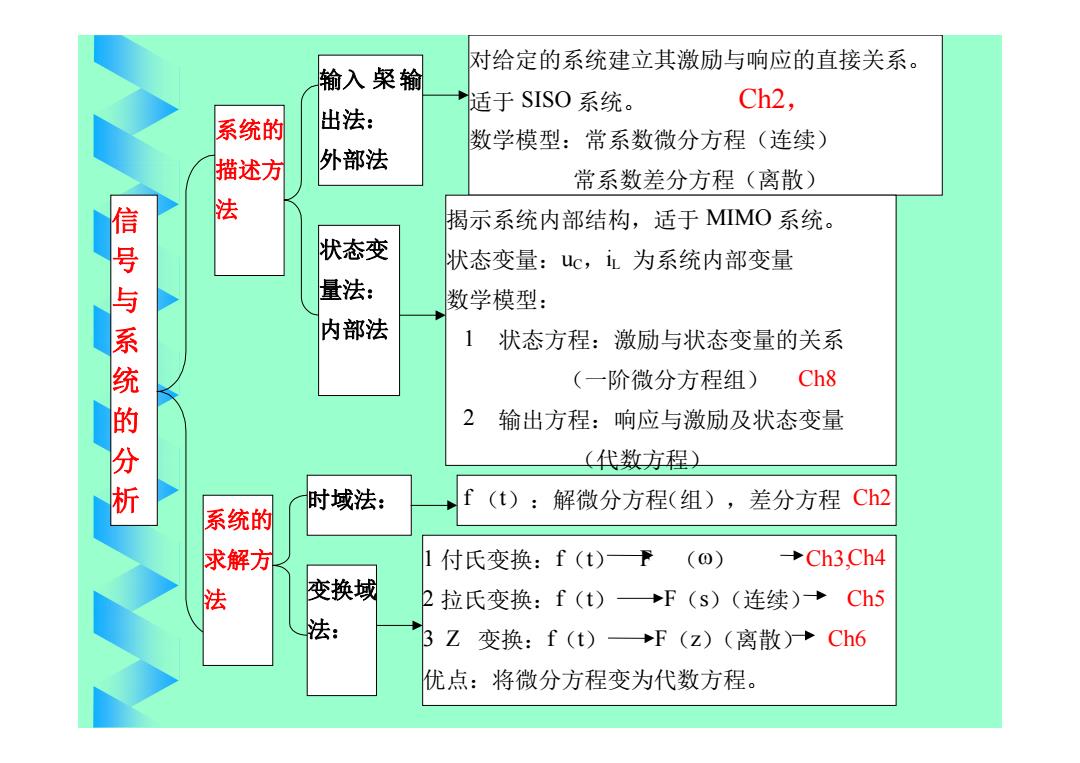
对给定的系统建立其激励与响应的直接关系。 输入梷输 适于SISO系统。 Ch2, 系统的 出法: 数学模型:常系数微分方程(连续)》 描述方 外部法 常系数差分方程(离散) 法 揭示系统内部结构,适于MMO系统。 状态变 状态变量:uc,i立为系统内部变量 信号与系统的分析 量法: 数学模型: 内部法 1状态方程:激励与状态变量的关系 (一阶微分方程组) Ch8 2 输出方程:响应与激励及状态变量 (代数方程) 时域法: f (t):解微分方程(组), 差分方程Ch2 系统的 求解方 1 付氏变换:f(t)下 (0) →Ch3Ch4 法 变换域 2拉氏变换:f(t)→F(s)(连续)→Ch5 法: BZ变换:f(t)→F(z)(离散) Ch6 优点:将微分方程变为代数方程
信 号 与 系 统 的 分 析 系统的 描述方 法 输入 梷 输 出法: 外部法 对给定的系统建立其激励与响应的直接关系。 适于 SISO 系统。 Ch2, 数学模型:常系数微分方程(连续) 常系数差分方程(离散) 状态变 量法: 内部法 揭示系统内部结构,适于 MIMO 系统。 状态变量:uC,iL 为系统内部变量 数学模型: 1 状态方程:激励与状态变量的关系 (一阶微分方程组) Ch8 2 输出方程:响应与激励及状态变量 (代数方程) 系统的 求解方 法 时域法: f (t):解微分方程(组),差分方程 Ch2 变换域 法: 1 付氏变换:f(t) F () Ch3, 2 拉氏变换:f(t) F(s)(连续) Ch5 3 Z 变换:f(t) F(z)(离散) Ch6 优点:将微分方程变为代数方程。 Ch4

§1一1信号及其分类 信号的描述 信号的描述 物理上:信号是信息寄寓变化的形式 数学上:信号是一个或多个变量的函数 2形态上:信号表现为一种波形 自变量 时间、位移 周期、 频率、幅度、相位
§1-1信号及其分类 信号的描述 物理上: 信号是信息寄寓变化的形式 数学上: 信号是一个或多个变量的函数 形态上:信号表现为一种波形 自变量 时间、位移 周期、频率、幅度、相位 一 ,信号的描述

信号的基本形式是:? 答 随时间变化的电压或电流 信号常可以表示为时间的函数或序列该函数的 图像称为信号的波形.í(t),í(《,y,t) 空域
信号的基本形式是: ? 答: 随时间变化的电压或电流. 信号常可以表示为时间的函数或序列,该函数的 图像称为信号的波形. f(t),f(x,y,t) 空域
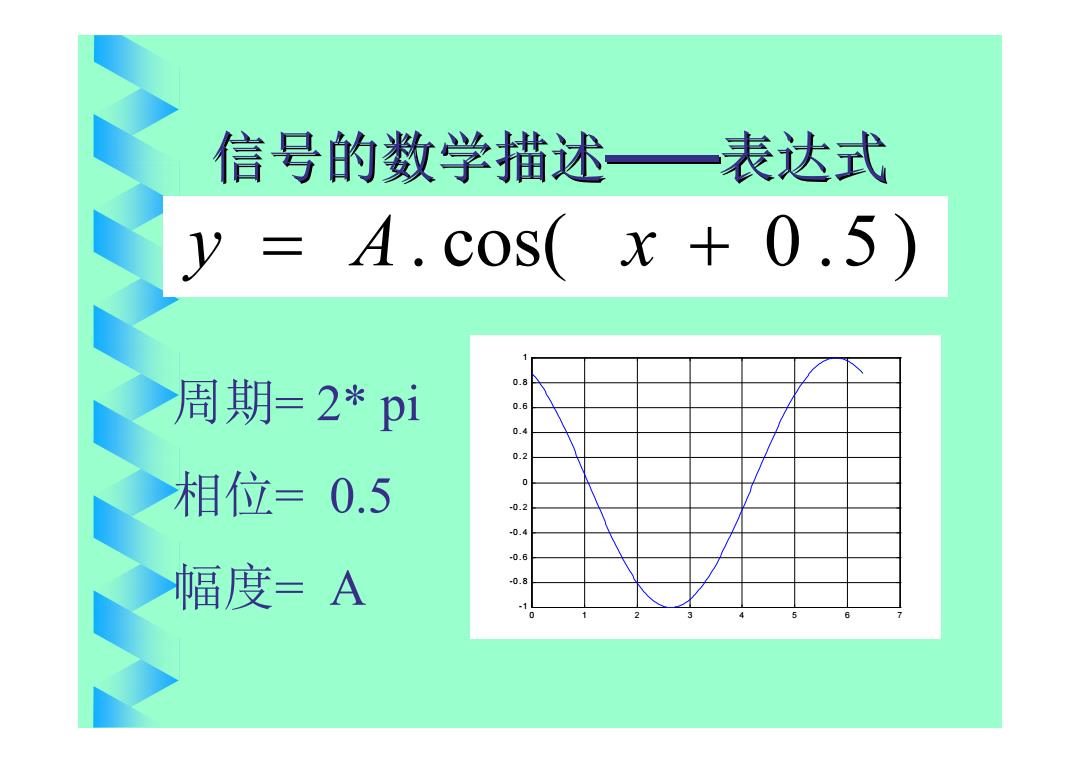
信号的数学描述 一表达式 y=A.c0s(x+0.5) 周期=2*pi 0.6 0.4 0.2 相位=0.5 0 -0.2 -0.4 -0.6 幅度=A 0.8
信号的数学描述——表达式 y A. cos( x 0 .5 ) 0 1 2 3 4 5 6 7 -1 -0. 8 -0. 6 -0. 4 -0. 2 0 0. 2 0. 4 0. 6 0. 8 1 周期= 2* pi 相位= 0.5 幅度= A