
理大学改写上式可得Loi?Cou22F这就1L恒等于电场能量导线单位长度所具有的磁场能量是电磁场传播过程的基本规律;这也是说:电压波和电流波沿导线传播的过程就是电磁能量的传播过程;Loi2导线单位长度的总能量为C.或山东理工大学电气与电子工程学院
◼ 导线单位长度所具有的磁场能量 恒等于电场能量 ,这就 是电磁场传播过程的基本规律; ◼ 这也是说:电压波和电流波沿导线传播的过程就是电磁能量 的传播过程; ◼ 导线单位长度的总能量为 或 2 0 2 0 2 1 2 1 L i = C u 2 0 L i 2 C0 u L i v 2 0 2 1 C u v 2 0 2 1 改写上式可得

大学ANDNaTSHE波过程的物理概念电磁场理论:在导线周围建立电场和磁场,由近及远以一定速度传播的过程电路理论:电源由近及远由导体对地电容和导体电感的冲放电过程电压波一与电场有关的电压-Cou-电流波一一与磁场有关的电流山东理工大学电气与电子工程学院
波过程的物理概念 ◼ 电磁场理论:在导线周围建立电场和磁场,由近及远以一定速度传 播的过程 ◼ 电路理论:电源由近及远由导体对地电容和导体电感的冲放电过程 电压波——与电场有关的电压 电流波——与磁场有关的电流 2 0 1 2 C u2 0 1 2 L i
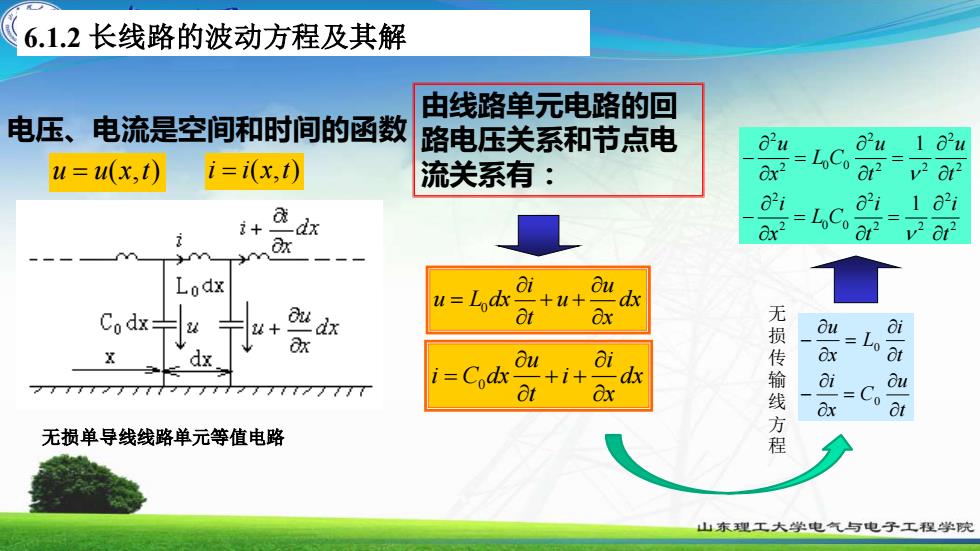
6.1.2长线路的波动方程及其解由线路单元电路的回电压、电流是空间和时间的函数路电压关系和节点电a'ua'ua'u1L.Coorari=i(x,t)112u=u(x,t)流关系有:iiIaL.Co7ardixaxor?3 +'MaxaiauLodxdxu=Lodx1Lataxaru无损传输线方程rodxdxauu+Laox+axaiouXdxdxi=Codx+i+i10at777Coatax无损单导线线路单元等值电路山东理工大学电气与电子工程学院
6.1.2 长线路的波动方程及其解 无损单导线线路单元等值电路 2 2 2 2 2 2 2 0 0 2 2 2 2 2 2 2 0 0 1 1 u u u L C x t t i i i L C x t t − = = − = = 由线路单元电路的回 路电压关系和节点电 流关系有: 0 i u u L dx u dx t x = + + 0 u i i C dx i dx t x = + + 电压、电流是空间和时间的函数 u = u(x,t) i = i(x,t) t u C x i t i L x u = − = − 0 0 无 损 传 输 线 方 程
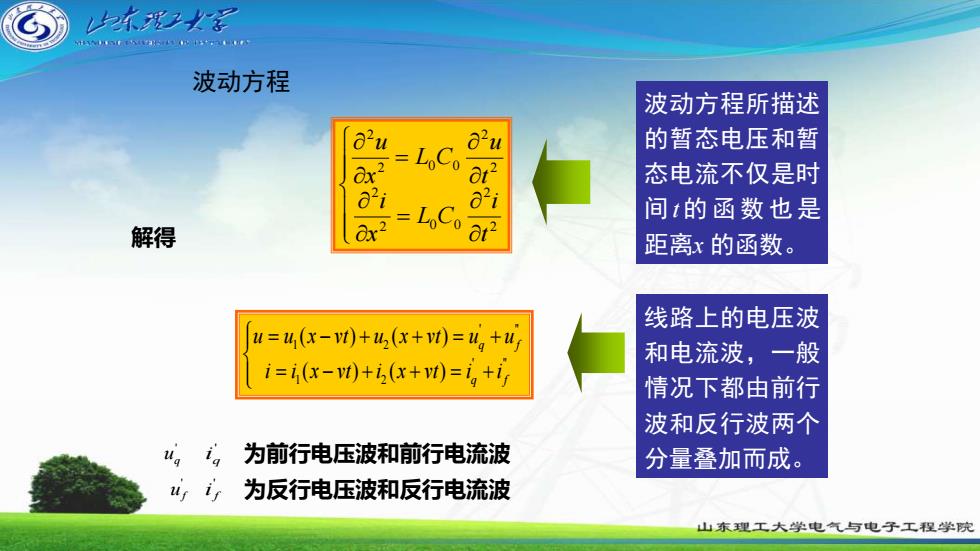
学波动方程波动方程所描述au的暂态电压和暂a1aiaLoCo1%态电流不仅是时间的函数也是LoCax2解得距离x的函数。线路上的电压波u=u(x-vt)+u(x+vt)=u.+u和电流波,一般i=i(x-vt)+i(x+vt)=i, +i,情况下都由前行波和反行波两个为前行电压波和前行电流波A分量叠加而成为反行电压波和反行电流波uf山东理工大学电气与电子工程学院
解得 为前行电压波和前行电流波 为反行电压波和反行电流波 = = 2 2 2 0 0 2 2 2 2 0 0 2 t i L C x i t u L C x u ' " 1 2 ' " 1 2 ( ) ( ) ( ) ( ) q f q f u u x vt u x vt u u i i x vt i x vt i i = − + + = + = − + + = + ' uq ' q i ' u f ' f i 波动方程所描述 的暂态电压和暂 态电流不仅是时 间t的函数也是 距离x 的函数。 波动方程 线路上的电压波 和电流波,一般 情况下都由前行 波和反行波两个 分量叠加而成

学ANDDEaSTStu(x,t)=u(x-vt)+u(x+vt)t=tt=ti(x,t)==[u (x-v)-u (x+v)(-)u(g-vis)=i(x-vt)+i(x+vt)而2Tu,(x-vt)的传播图13JLCui(x-vt)是随着时间的增加,以速度v向x增加的方向运动的,是前行波电压;u2(x+vt)是随着时间的增加,以速度v向x负方向运动,是反行波电压。山东理工大学电气与电子工程学院
( ) ( ) ( ) ( ) 1 2 1 2 ( , ) 1 ( , ) [ ] u x t u x vt u x vt i x t u x vt u x vt Z = − + + = − − + = − + + i x vt i x vt 1 2 ( ) ( ) 0 0 1 L C v = ◼ u1 (x-vt) 是随着时间t的增加,以速度v向x增加的方向运动的,是前行波电压; ◼ u2 (x+vt) 是随着时间t的增加,以速度v向x负方向运动,是反行波电压。 u1 (x-vt)的传播图