
-2 1-2 例2:求对称矩阵A所对应的二次型A= √3 1 0 解:f(x1,x2,x3) 0 -1 =-2x+x2-x+2W3x水2+xx3 例3:已知二次型f的秩为2,求参数c。 f(x,x2,x3)=5x+5x号+c号-2x2+6.x63-6x53 .r(A)=2 解:A= -1 5 -3 ∴.A=0 3-3 ∴.C=3
1 2 3 2 3 1 0 1 0 1 2 A = - - 例2:求对称矩阵 A 所对应的二次型。 1 2 3 2 2 2 1 2 3 1 2 1 3 ( , , ) 2 2 3 f x x x = − + − + + x x x x x x x 解: ( ) 2 0 3 r A A c = = = 例3:已知二次型 的秩为2,求参数c。 2 2 2 1 2 3 1 2 3 1 2 1 3 2 3 f x x x x x cx x x x x x x ( , , ) 5 5 2 6 6 = + + − + − f 5 1 3 1 5 3 3 3 A c − = − − − 解:
2.对于二次型f=XAX,若存在可逆线性变换 X1=Cy1+C2Jy2+.+Cmyn x2=c2y+c2y2++cany =cy+C2y2++Cmy 线性变换,记作 (2) Cu 系数 C= 22 X= Y= y2 矩阵 Cn2 则线性变换(2)可记作:X=CY
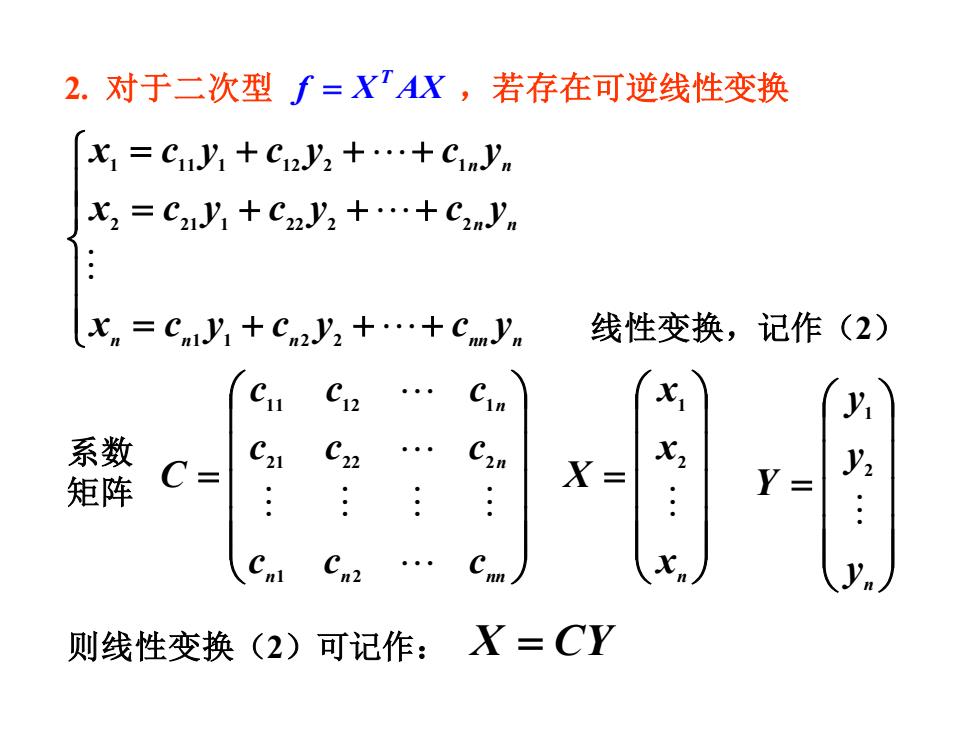
2. 对于二次型 ,若存在可逆线性变换 = + + + = + + + = + + + n n n nn n n n n n x c y c y c y x c y c y c y x c y c y c y 1 1 2 2 2 21 1 22 2 2 1 11 1 12 2 1 系数 矩阵 = n n nn n n c c c c c c c c c C 1 2 21 22 2 11 12 1 = n x x x X 2 1 = n y y y Y 2 1 线性变换,记作(2) 则线性变换(2)可记作: X = CY T f X AX =

若C是可逆矩阵,则称线性变换 (2)是非退化线性变换 若C是正交矩阵,则称线性变换(2)是正交线性变换 对于二次型,我们讨论的主要问题是:寻求可逆的线性变换 使二次型只含平方项. 即二次型∫=XTAX=∑x,x i,i=l 经过可逆线性变换X=CY 使得f=ky+k2y2+.+ky月 这种只含平方项的二次型,称为二次型的标准型
若C 是可逆矩阵,则称线性变换(2)是非退化线性变换 若C 是正交矩阵,则称线性变换(2)是正交线性变换 对于二次型,我们讨论的主要问题是:寻求可逆的线性变换 使二次型只含平方项. , 1 n T ij i j i j f X AX a x x = 即二次型 = = 经过可逆线性变换 X = CY 这种只含平方项的二次型,称为二次型的标准型 2 2 2 1 1 2 2 n n 使得 f k y k y k y = + + +

3.矩阵的合同 二次型f=X”AX 经过非退化线性变换 X-CY 可化为f=XAX=(CY)'A(CY)=Yr(CAC)M 则,二次型f的矩阵由A变为CAC 令B=CrAC 则 (1) B=CAC仍是对称矩阵 (2) r(B)=r(A)
3. 矩阵的合同 f X AX T 二次型 = 经过非退化线性变换 X = CY 可化为 f X AX (CY ) A(CY ) T T = = Y C AC Y T T = ( ) f A C AC 则,二次型 的矩阵由 变为 T (2) ( ) ( ) (1) r B r A B C AC T = 则 = 仍是对称矩阵 B C AC T 令 =