海南大学：《线性代数》课程教学资源（PPT课件）第六章 二次型

41七1+412X2+.+a1n火m 21X1+22X2+.+42mXn =(x1,x2,xn) mK1+0n2x2+.+0nmXn 12 . 1 L21 L22 X2 =(1,x2.,xn) ·:

11 1 12 2 1 21 1 22 2 2 1 2 1 1 2 2 ( , , , ) n n n n n n n nn n a x a x a x a x a x a x x x x a x a x a x   + + +   + + +   =     + + +   11 12 1 1 21 22 2 2 1 2 1 2 ( , , , ) n n n n n nn n a a a x a a a x x x x a a a x          =         

L12 令A= u21 L22 a2n X= X2 Ani An2 Xn 则f=XIAX 二次型的矩阵表示 其中A为对称矩阵。 例如：二次型f(x,x2,x3)=x2-3y32-4x水2十x2x -2 0 1 =(x1,x2,x3) -2 0 0 1 3 2

1 2 n x x X x       =       11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a     =         令 T 则 f X AX = 其中 A 为对称矩阵。 二次型的矩阵表示 1 1 2 3 2 3 1 -2 0 1 ( , , ) -2 0 2 1 0 -3 2 x x x x x x         =              2 2 1 2 3 1 3 1 2 2 3 例如：二次型 ( , , ) 3 4 f x x x x x x x x x = − − +

在二次型的矩阵表示中， 任给一个二次型，就唯一确定一个对称矩阵； 反之，任给一个对称矩阵，也可唯一确定一个二次型. 这样，二次型与对称矩阵之间存在一一对应的关系. 定义2： 二次型f=XTAX 把对称矩阵A称为二次型f的矩阵 也把二次型f称为对称矩阵A的二次型 对称矩阵A的秩称为二次型f的秩

在二次型的矩阵表示中， 任给一个二次型，就唯一确定一个对称矩阵； 反之，任给一个对称矩阵，也可唯一确定一个二次型． 这样，二次型与对称矩阵之间存在一一对应的关系． 把对称矩阵 A 称为二次型 f 的矩阵 也把二次型 f 称为对称矩阵 A 的二次型 对称矩阵 A 的秩称为二次型 f 的秩 T 定义2： 二次型 f X AX =

例1：求二次型f的矩阵 (1)f(x,y,z)=x+2x-2xK2+3x2x3 -1 0 解： 2 3-2 (2)f(x1,K2,3,x4)=x子+2x2+7x-2xK2-2x2x3+4x3x4 0 0 -1 0 解： 0 2 2

2 2 1 2 1 2 2 3 (1) ( , , ) 2 2 3 f x y z x x x x x x = + − + 例1：求二次型 f 的矩阵 1 1 0 3 1 2 2 3 0 0 2 A     −   = −          解： 222 1 2 3 4 1 2 4 1 2 2 3 3 4 (2) ( , , , ) 2 7 2 2 4 f x x x x x x x x x x x x x = + + − − + 1 1 0 0 1 2 1 0 0 1 0 2 0 0 2 7 A   −   − − =     −     解：

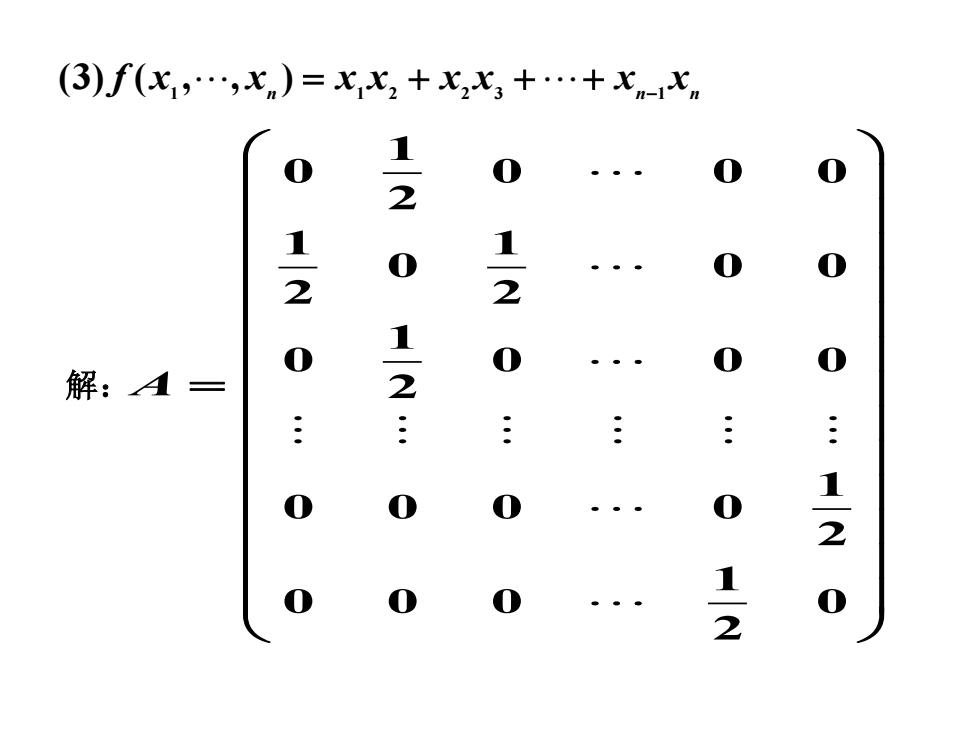
(3)f(X1,.,xn)=X2+2x3+.+Xm-七， 1 2 解：A 2

x x n x x x x x n x n f 1 1 2 2 3 1 (3) ( , , )  = + ++ − 1 0 0 0 0 2 1 1 0 0 0 2 2 1 0 0 0 0 2 1 0 0 0 0 2 1 0 0 0 0 2 A     =   解：