
32 一、《高等数学》(第七版)下册习题全解 共面。 设c=Aa+ub,则 (-3,12,6)=A(-1,3,2)+4(2,-3,-4) =(-A+2μ,3A-3μ,2A-4μ) r-A+2u=-3. 即 3A-3u=12, 2A-4u=6. 解得A=5,4=1.故 c=5a+b. @14.已知动点M(x,y,)到x0y平面的距离与点M到点(1,-1,2)的距离相等,求点 M的轨迹的方程. 解根据题意知 |2|=(x-1)2+(y+1)2+(2-2)2, 即(x-1)2+(y+1)2-4(:-1)=0为点M的轨迹的方程. 15.指出下列旋转曲面的一条母线和旋转轴: (1)z=2(x2+y2): .y22 (3)2=3(x2+y2): ( 解(1)母线为=0, 旋转轴为:轴. 1z=2y2 rx=0. (2)母线为,2,2 旋转轴为y轴 9+36=1 (3)母线为=0, 旋转轴为:轴. :=3y. 2=0, (4)母线为 ,旋转轴为x轴 四16.求通过点A(3,00)和B(0.0,1)且与x0面成,角的平面的方程. 解设所求平面方程为。++= 平面过点A(3.0.0),B(0.0.1).故a=3,c=1.这样平面方程为 行+6+:=l

第八章向量代数与空间解析几何 它与x0y面成:角,故 3方小(0.0,1) 11 ( 即 (+(+1=4,名± 故所求平面为 x+√26y+3z=3或x-√26y+3z=3. @17.设一平面垂直于平面:=0,并通过从点1,-1,)到直线-+1=0的垂线。 1x=0 求此平面的方程. 解直线-:+1=0的方向向量 1x=0 s=01-1=(0,-1,-1). 100 作过点(1,-1,1)且以s=(0,-1,-1)为法向量的平面: -1·(y+1)-(:-1)=0,即y+z=0, rJ-2+1=0 联立x=0, 得垂足0,宁》 y+z=0 所求平面垂直于平面z=0,设平面方程为Ax+By+D=0.平面过点(1,-1,1)及 [A-B+D=0. -2B+D=0, 由此解得B=2D,A=D.因此所求平面方程为Dx+2Dy+D=0,即 x+2y+1=0. 面18求过点(-10,4).且半行于平面3x-4+:-10=0,又与直线:3-号 相交的直线的方程 解设所求直线方程为 x+l-y-0.=4

34 一、《高等数学》(第七版)下册习题全解 所求直线平行于平面3x-4y+z-10=0,故有 3m-4n+p=0, (1) 又所求直线与直线十3号相交放有 1 -1-(-1)3-00-4 112=0, m n p 即 10m-4n-3p=0. (2) 联立(1)(2)式可得 161928 m n p 因此所求直线方程为 x+ 6 若两直线46骨交时与 n PI 必共面,故 M1M2·(s1×52)=0 x?-12-32-1 即有 m1n1P1=0. m2 P 因19.已知点A(1,0,0)及点B(0,2,1),试在:轴上求一点C,使△ABC的面积最小 解所求点位于:轴,设其坐标为C(0.0,:),由向量的几何意义知 5aAc=分1店xA花1. i j ki j k AB xAC=0-12-01-0=-121 0-10-02-0-10: =2:i+(a-1)j+2k, 华 sae=222+(:-12+2-52-2+5 设:)=5好2-2+5,则由e)=0:-2=0得:=行四/()=0>0.放9 :=行时,△MBC的面积取对极小值.山于班点唯,放:=即G的坐标为

第八章向量代数与空间解析几何 35 0.0.5)时,Sac最小 20,求曲线=2-2-y片, 文{:=(怎-1)2+,-1)在三个坐标面上的投影曲线的方程 解在=2-, {=(-1)+-1)中清去得2-2-2=(-12+0-1,即 产+-,=0.故-y=0为曲线在0面上的投影衡线方程 :=0 ,在二2、,12申消去,待=(x1)2+(±2-:1)2即 222+-4x-35+2=0.故22+-4-3:+20为前线在0面上 ly=0 的投影曲线方程。 网限.可得2242:+:-4y-3:+2=0它就是曲线在)0:面上的投影曲线 x=0. 方程. 21.求锥面:=√2+y2与柱面2=2x所围立休在三个坐标面上的投影, 解 在=+了中清去得2x=2+即(-1)2+y=1,做立体在0 2=2x 面上的授竖为:)户+1(如附8-20 1=0 而该立体在0:面上的投影为:≤:≤,2·(如图8-20,在)0:百上的投影 y=0 x=0. 图8-20
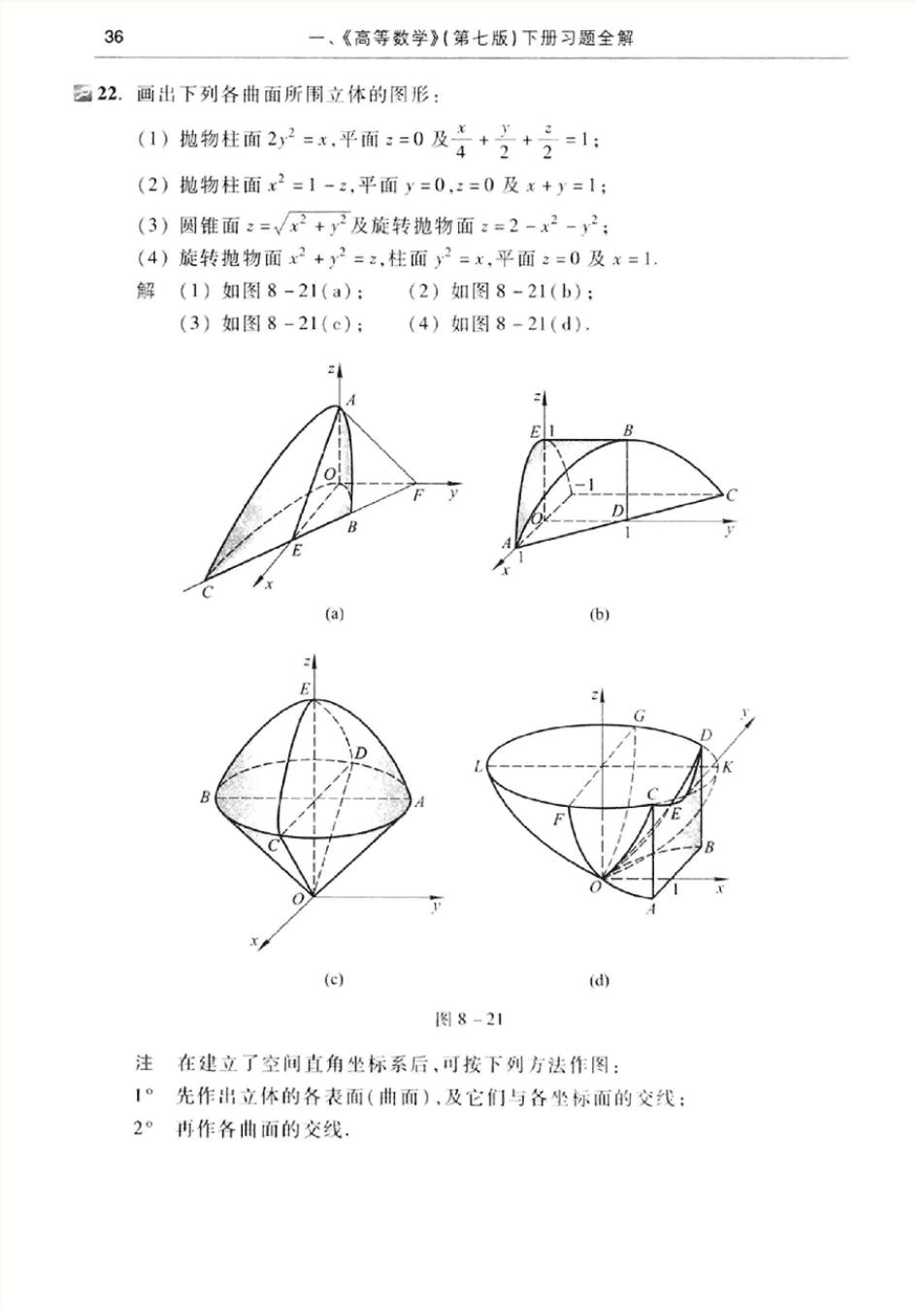
36 一、《高等数学(第七版)下册习题全解 西22.画出下列各曲面所围立体的图形: (1)抛物柱面2y2=,平面:=0及4+之+氵=1: (2)抛物柱面x2=1-,平面y=0,:=0及x+y=1: (3)圆锥面:=√+了及旋转抛物面:=2-x2-y2: (4)旋转抛物面x2+y2=2,柱面y2=x.平面:=0及x=1. 解(1)如图8-21(a):(2)如图8-21(b): (3)如图8-21(c);(4)如图8-21(d) b (c) 图8-21 注在建立了空间直角坐标系后,可按下列方法作图: 1。先作出立体的各表面(曲而),及它们与各坐标面的交线: 2°再作各曲面的交线