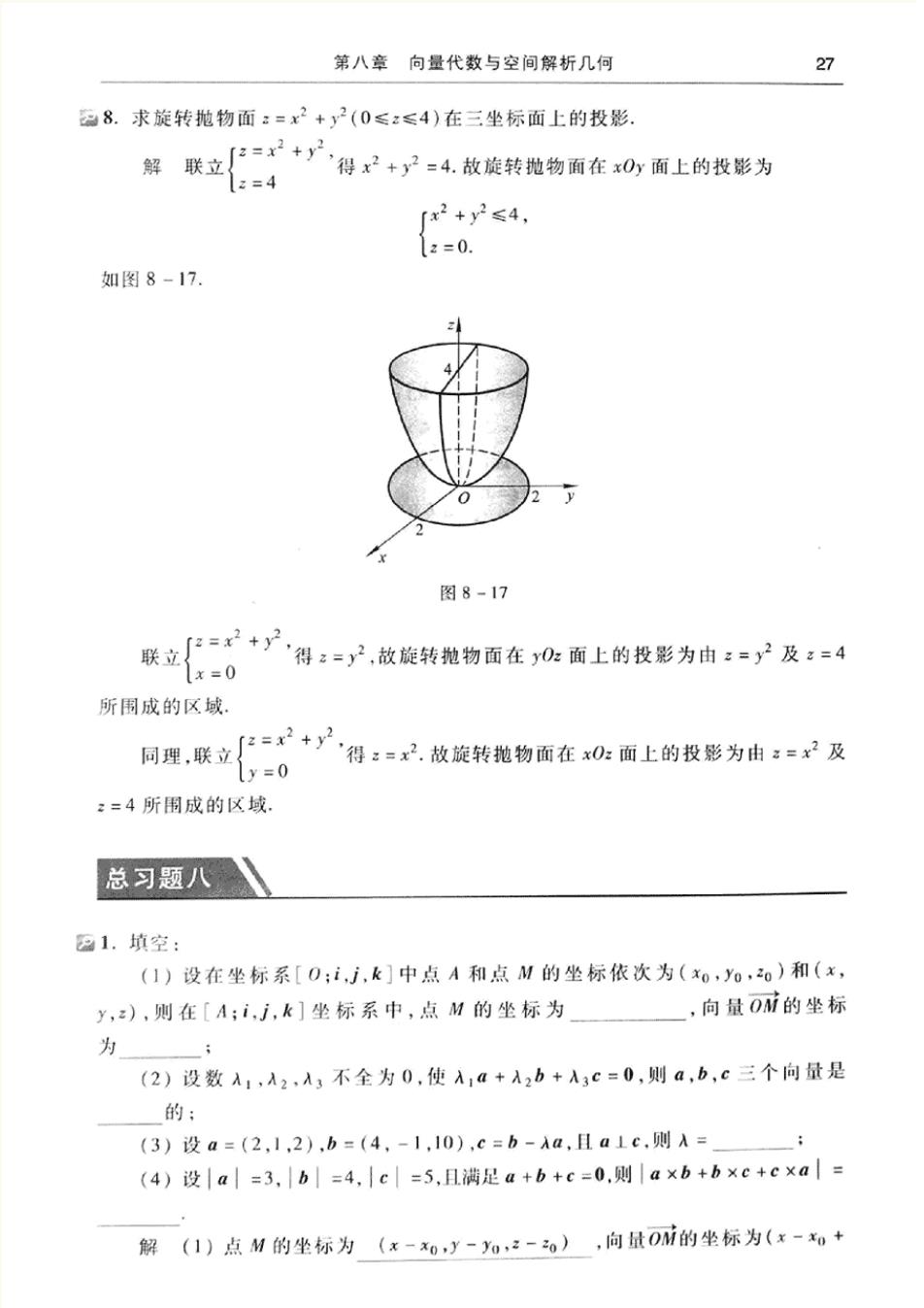
第八章向量代数与空间解析几何 27 28.求旋转抛物面:=x2+y2(0≤:≤4)在三坐标面上的投影 解联立+产得2+y产:4.故旋转粒物面在0面上的投影为 1z=4 「x2+y2≤4, 1z=0. 如图8-17. 图8-17 联立+户得:=,故旋转抛物面在面上的投影为由:=)及:4 1x=0 所围成的区域。 同理。联立:+,得:=品,故旋转范物面在0:面上的投影为由:子及 ly=0 :=4所围成的区域 总习题八 21.填空: (1)设在坐标系[O;i,j,k]中点A和点M的坐标依次为(x0,yo,0)和(x, y,),则在[A;i广,k]坐标系中,点M的坐标为 ,向量O的坐标 为 (2)设数A1,A2,A,不全为0,使A1a+A2b+A3c=0,则a,b,c三个向量是 的: (3)设a=(2,1,2),b=(4,-1,10),c=b-Aa,且a1c,则A= (4)设|a|=3,|b|=4,|c=5,且满足a+b+c=0,则|a×b+b×c+c×a|= 解(1)点M的坐标为(x-0y-),向量0的坐标为(x-+

28 一、《高等数学》(第七版)下册习题全解 x0y-J0+y0,2-20+0)=(x,y,2) (2)由[(A1a+A,b+A,c)×b]·c=0得(a×b)·c=0.即a,b,c共面. (3)c=b-Aa=(4,-1,10)-A(2.1.2)=(4-2A,-1-A,10-2A). a1c,故a·c=(2,1,2)·(4-2A,-1-A.10-2A)=27-9A=0,从而A=3 (4)由(a+b+c)×b=0知a×b+c×b=0,即a×b=b×c: 由(a+b+c)×a=0知b×a+c×a=0,即axb=c×a. 又,由a|2+b|2=c|2知以向量a,b,c为边的三角形为直角三角形.且 a1b.故 |a×b+b×c+c×a=3|a×b=3 ab sin(a.b) =3×3×4×1=36. 密2.下列两题中给出了四个结论,从中选出一个正确的结论: ()设直线L的方程为-y+:=1, 则L的参数方程为( 2x+y+2=4, x=1-21, r=1-21. x=1-24. rx=1-24. (A)y=1+t,(B) y=-1+1,(C)y=1-1,(D)y=-1-t, lz=1+31 【z=1+31 :=1+3 :=1+31 (2)下列结论中,错误的是(). (A):+2x2+y2=0表示椭圆抛物面 (B)x2+2y2=1+3:2表示双叶双曲面 (C)x2+y2-(:-1)2=0表示圆锥面 (D)y2=5x表示抛物柱面 解(1)应选(A).直线1的方向向量为8=(-2,1.3),过点(1.1.1) (2)应选(B).x2+2)2=1+3:2表示单叶双曲面。 23.在y轴上求与点A(1,-3,7)和点B(5,7,-5)等距离的点 解根据题意,设所求点为M(0,y,0),由 12+(y+3)2+72=52+(y-7)2+(-5)2 得y=2.故所求点为M(0.2.0). 4.已知△ABC的顶点为A(3,2,-1).B(5,-4.7)和C(-1.1.2),求从顶点C所引 中线的长度. 解设AB中点的坐标为(x00,o),由 5421.7 从而顶点G所引中线的长度 d=(4+1)2+(-1-1)3+(3-2)=30. a5.设△ABC的三边BC=a.C=b.A店=c.三边中点依次为D.E.F.试用向量a.b.c

第八章向量代数与空间解析几何 29 表示AD.BE.CF,并证明 AD+B正+C求=0. 证如图8-18,D,E,F分别为BC,CA,AB的中点,因此 励:配:号,正d安亦丽=号 从而 市:店+丽+受 成=配+店=a+安 C=C+=b+, 故币+庇+序=c+号+a+名+b+号=2(a+b+e)=0, ✉6.试用向量证明三角形两边中点的连线平行于第三边,且其长度等于第三边长度 的一半. 证如图8-19,D,E分别是CA与BC的中点, 由A店=A元+CB=2(D元+C正)=2D正知 AB∥D成且1成1=?11 即三角形两边中点的连线平行于第三边,且长度等于第三边长度的一半 图8-18 图8-19 a7.设|a+b|=|a-b,a=(3,-5,8),b=(-1,1,2),求 解a+b=(3-1,-5+1,8+z)=(2,-4,8+z), a-b=(3-(-1),-5-1,8-z)=(4,-6,8-z), 由|a+b|=a-b|知 √/22+(-4)2+(8+)7=2+(-6)2+(8-)2】 经整理得z=1. 8.设|a=3,|b|=1.(a,b)=石,求向量a+b与a-b的夹角 解a+b|2=(a+b)·(a+b)=|a|2+|b|2+2|a川b|cos(a,b)

30 一、《高等数学》(第七版】下册习题全解 =(62+12+251君 =4+257 |a-b|2=(a-b)·(a-b)=a|2+1b2-2ab|cos(a,b) =(5)2+12-251o6 =4-25.5=1. 2 (a+b)·(a-b)=a2-1b2=3-1=2. cos(a+ba-b)=a+b):(a-b2.2.2 1a+ba-bT万.1万 所以(a+b,a-b)=arccos 2 分 9.设a+3b17a-5b,a-4b17a-2b,求(a,b) 解由a+3b17a-5b知(a+3b)·(7a-5b)=0.由a-4b17a-2b知(a- 4b)·(7a-2b)=0,故 7|a2+16a.b-15|b2=0 (1) 71a|2-30a·b+81b|2=0. (2) 两式相诚得46ab=23b2,即a·b=子b2,代人(1)式得 al=b. 从而 wao:i&6t- 所以 (a,b)=于 西10.设a=(2,-1,-2),b=(1,1,2),问:为何值时(a,b)最小?并求出此最小值 解w(a6=iV2-(-2+ a·b (2.-1.-2)·(1.1.) 1-2z 32+ 设0)=1-2 32+·则

第八章向量代数与空间解析几何 -22+2-(1-2z) 2+ 2+2 =}2+ -4-2 令()=0得:=-4. 由于0≤(a,b)≤时,eos(a,b)为单调减少函数.f(:)取得最大值时. 0=(a,b)达到最小值 经验证:=-4时,f(z)达到最大值,此时0=(a,b)达到最小值且由 s(abn=9知8n=mm竖- 1.设a=4,b=3,(a,b)=石,求以a+2b和a-36为边的平行四边形的 而积. 解根据向量积的儿何意义知以a+2b和a-3b为边的平行四边形的面积 s=|(a+2b)×(a-3b)l =5|a×b|=5|a川b|sin(a,by =5x4x3xm=5x4×3×-30 12.设a=(2,-3,1),b=(1,-2,3),c=(2,1,2),向量r满足r1a,r1b,P可jr= 14,求r. 解设向量r=(x,y,2) 由r1a知r·a=0.即 2x-3y+:=0. hr1b知r·b=0.即 x-2y+3:=0. 由-后=14知 2x+y+2z=14|c|=14×3=42. 联立上述三个方程得x=14,y=10,:=2.故r=(14,10,2) 13.设a=(-1,3,2),b=(2,-3,-4).c=(-3.12.6),证明三向量a,b,c共面 并用a和b表示c. -132 证由(a×b)·c=2-3-4=0知abc]=0,故三个向量a,b,c -3126