西安交通大学：《电磁场与电磁能》课程教学资源（PPT课件）第一章 静电场

AKKDB）高斯定律的积分形式V.D=p[V.DdV= (pd散度定理fD.ds=ZqD的通量与介质无关，但不能认为D的分布与介质无关。D,·ds=(q)思考D,-ds= (q )qD,=D,=D,=X4元图1.2.18点电荷的电场中置入任意一块介质D通量只取决于高斯面内的自由电荷，而高斯面上的D是由高斯面内、外的系统所有电荷共同产生的。图1.2.19点电荷土q分别置于金属球壳的内外

  = S1 D1 dS ( )   = S2 D2 dS ( ) 1 2 3 2 4 r q  D = D = D = ( ) q q D 的通量与介质无关，但不能认为D 的分布与介质无关。 D 通量只取决于高斯面内的自由 电荷，而高斯面上的 D 是由高斯面内、 外的系统所有电荷共同产生的。 B） 高斯定律的积分形式  D =  dV dV V V  D =   d =q S D S 散度定理 图1.2.19 点电荷±q分别置于金属球壳的内外 图1.2.18 点电荷的电场中置入任意一块介质

合KD4.高斯定律的应用高斯定律适用于任何情况，但只有具有一定对称性的场才能得到解析解计算技巧：a）分析给定场分布的对称性，判断能否用高斯定律求解b）选择适当的闭合面作为高斯面，使D·ds容易积分。例1.2.2求电荷线密度为T的无限长均匀带电体的电场。P解：电场分布特点：。D线皆垂直于导线，呈辐射状态；等r处D值相等；取长为L，半径为r的封闭圆柱面为高斯面。图1.2.20电荷线密度为T的无限长均匀带电体由 fD.ds=q,得D.ds=o.D,.dS, +T2SD,·2元rL= tLD=E,e2元r2元680

例1.2.2 求电荷线密度为  的无限长均匀带电体的电场。 解：电场分布特点： • D 线皆垂直于导线，呈辐射状态； • 等 r 处D 值相等； 取长为L，半径为 r 的封闭圆柱面为高斯面。 d q, S  =  由 D S 得 D1 2rL =L r 2 r D e   1 = r 0 e D E 2 r0 1 1     = =      =  +  +  S1 2 S2 3 3 S 1 1 2 2 S D dS D dS D dS D dS = L 图1.2.20 电荷线密度为  的无限长均匀带电体 4. 高斯定律的应用 计算技巧： a）分析给定场分布的对称性，判断能否用高斯定律求解。 b）选择适当的闭合面作为高斯面，使  DdS 容易积分。 • 高斯定律适用于任何情况，但只有具有一定对称性的场才能得到解析解

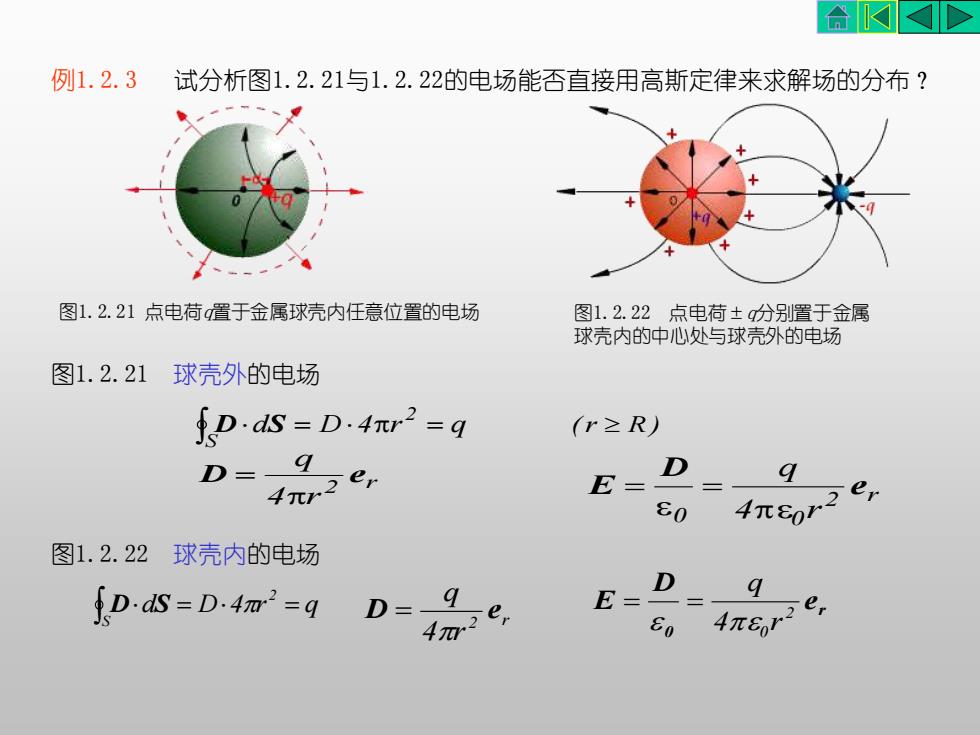
AKKD例1.2.3试分析图1.2.21与1.2.22的电场能否直接用高斯定律来求解场的分布？图1.2.21点电荷置于金属球壳内任意位置的电场图1.2.22点电荷±分别置于金属球壳内的中心处与球壳外的电场球壳外的电场图1.2.21fD.dS = D.4元r2 = q(r≥R)qDD=O4元r2erE:804元8图1.2.22球壳内的电场DqqE:D.dS=D.4m=q1D=-e4元6r4元280

图1.2.22 球壳内的电场 d D 4 r q 2 S  =  =  D S  r 0 e D E 2 0 4 r q    = = 2 r 4 r q D e  = 图1.2.21 球壳外的电场 d D 4 r q 2 S  =   =  D S 2 r 4 r q D e  = 2 r 0 0 4 r q e D E   =  = (r  R ) 例1.2.3 试分析图1.2.21与1.2.22的电场能否直接用高斯定律来求解场的分布？ 图1.2.21 点电荷q置于金属球壳内任意位置的电场 图1.2.22 点电荷±q分别置于金属 球壳内的中心处与球壳外的电场

合KKD1.3静电场的基本方程·分界面上的衔接条件1.3.1静电场的基本方程静电场是一个无旋、有源场，静止电荷就是静电场的源。这两个重要特性用简洁的数学形式为：VxE=0.E.dl=0(E=-Vβ)D.dS=qV.D=Pf(D=&E)例1.3.1已知A=3xe+4ye，+5ze，，试判断它能否表示个静电场？解：根据静电场的旋度恒等于零的性质，exeeaaaaAyOAyOA.aAxaA,oArVxA=yey)e-=0+axayOzOzOzaxaxayayAxA,A.对应静电场的基本方程V×E=0，量A可以表示一个静电场。时思考能否根据失量场的散度来判断该矢量场是否是静电场？

1.3 静电场的基本方程 • 分界面上的衔接条件 1.3.1 静电场的基本方程 静电场是一个无旋、有源场，静止电荷就是静电场的源。这两个重要特性用简 洁的数学形式为： E =0 =  f  D ( E = − ) ( D = E ) d 0 l  =  E l d q S  =  D S 解：根据静电场的旋度恒等于零的性质, x y z x y z A A A x y z       = e e e A z y x y x z x z y y A x A x A z A z A y A ( )e ( )e ( )e   −   +   −   +   −   = =0 例1.3.1 已知 A = 3xex + 4 yey + 5zez ， 试判断它能否表示个静电场？ 对应静电场的基本方程 E  0 ，矢量 A 可以表示一个静电场。 能否根据矢量场的散度来判断该矢量场是否是静电场?

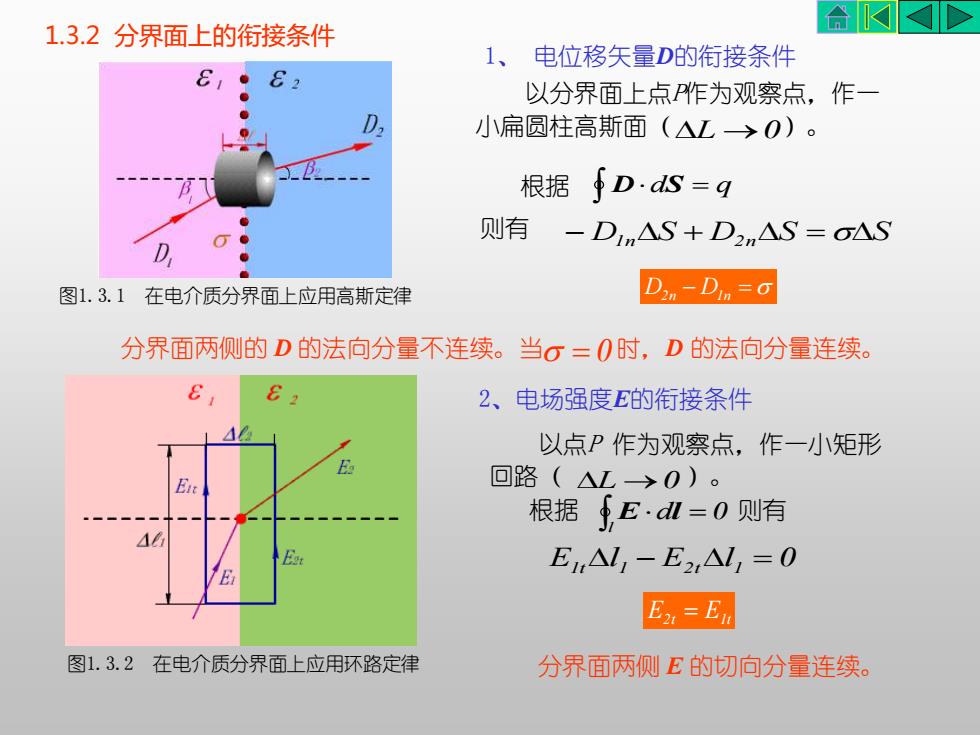
AKKD1.3.2分界面上的衔接条件1、电位移矢量D的衔接条件6182以分界面上点P作为观察点，作一D小扁圆柱高斯面（L→0）。根据 fD·ds=q则有 -DnAS+D2nAS=oASADD2n-Din=a图1.3.1在电介质分界面上应用高斯定律分界面两侧的D的法向分量不连续。当=0时，D的法向分量连续。82、电场强度E的衔接条件42以点P作为观察点，作一小矩形H回路（△→0）。E根据E·dl=0则有44EiN, -E2,N, = 0EaEE,=E图1.3.2在电介质分界面上应用环路定律分界面两侧E的切向分量连续

以分界面上点P作为观察点，作一 小扁圆柱高斯面（ L →0 ）。 D2n − D1n = 2、电场强度E的衔接条件 以点P 作为观察点，作一小矩形 回路（ L →0 ）。 E1t l 1 − E2t l 1 = 0 E2t = E1t 1.3.2 分界面上的衔接条件 1、 电位移矢量D的衔接条件 分界面两侧 E 的切向分量连续。 分界面两侧的 D 的法向分量不连续。当  = 0 时，D 的法向分量连续。 图1.3.2 在电介质分界面上应用环路定律 则有 − D1n S + D2n S =S d = q  根据 D S d 0 l  =  根据 E l 则有 图1.3.1 在电介质分界面上应用高斯定律