《线性代数》课程教学课件（PPT讲稿）第四章 线性方程组 4-2 齐次线性方程组

二、基础解系及其求法 由于方程组(4-5)的所有解，对于加法和数乘运算构 一个向量空间，也称为方程组(4-5)解空间. 下面我们来求解空间的一个最大线性无关组。 设线性方程组(4-5)系数矩阵A的秩为r,不妨假设A 的前个列向量线性无关，于是A的行最简形为 1 0b1r+1 bin 0 1 b I= r+l b 0 0 0 0 0 。 0 0 0

二、基础解系及其求法 由于方程组(4-5)的所有解,对于加法和数乘运算构 一个向量空间,也称为方程组(4-5)解空间. 下面我们来求解空间的一个最大线性无关组。 设线性方程组(4-5)系数矩阵A的秩为r,不妨假设A 的前r个列向量线性无关，于是A的行最简形为 1 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 r n rr rn b b b b I + +               =            

与对应的线性方程组为 +.+b=0 X,tbnXr41++b,nxn=0 移项后可得 =-B.r-bnXm (4-7) x,=-b4H火41-bnx

1 1, 1 1 1, , 1 1 , (4 7) r r n n r r r r r n n x b x b x x b x b x + + + +  = − −−     −  = − −−  与I对应的线性方程组为 1 1, 1 1 1, , 1 1 , 0 0 r r n n r r r r r n n x b x b x x b x b x + + + +  + + + =      + + + =  移项后可得

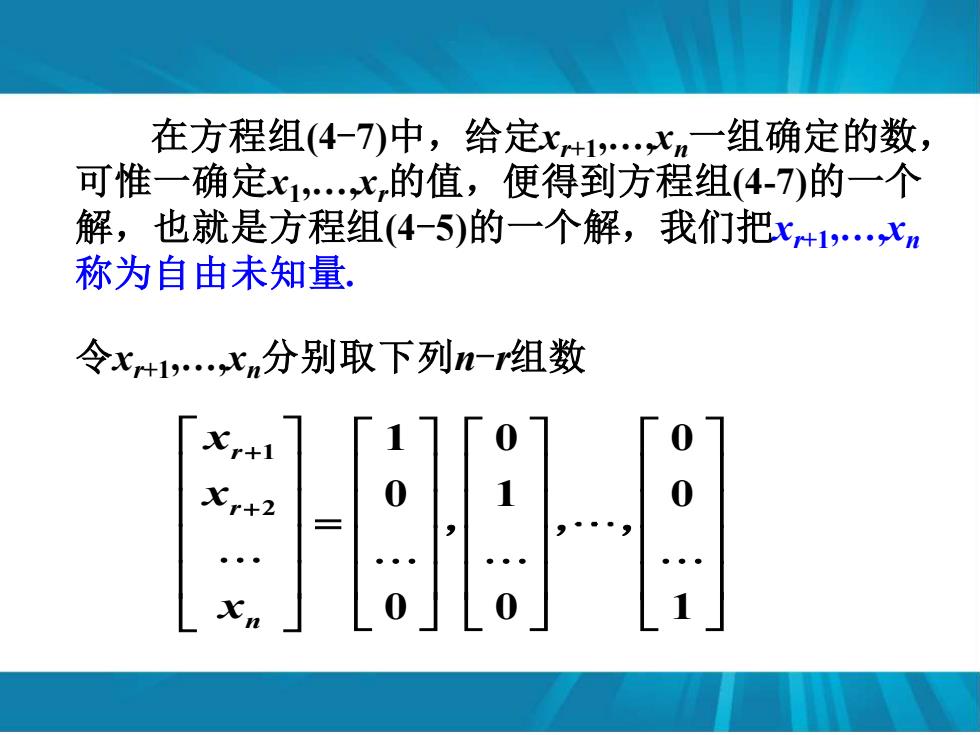
在方程组(4-)中，给定x+1,水n一组确定的数， 可惟一确定x1心，的值，便得到方程组(4-7)的一个 解，也就是方程组(4-5)的一个解，我们把x+1xm 称为自由未知量 令x+1,心n分别取下列-r组数

令xr+1,.,xn分别取下列n-r组数 1 2 1 0 0 0 1 0 0 0 1 r r n x x x + +                   =                                   ， ， ， 在方程组(4-7)中，给定xr+1,.,xn一组确定的数， 可惟一确定x1 ,.,xr的值，便得到方程组(4-7)的一个 解，也就是方程组(4-5)的一个解，我们把xr+1,.,xn 称为自由未知量

由(4-7)依次可得 x, -b 从而得到(4-7)也就是(4-5)的-个解 -b1,+1 bi.n 一br+1 -b*2 一brn 51= 1 52= 0 5-,= 0 0 1 0 0 0 1

1 1, 1 , 1 r r r r x b x b + +     −        =        −     ， 1, 2 , 2 r r r b b + +   −        −  ， 1, , n r n b b   −        −  ， 由(4-7)依次可得 . 从而得到(4-7)也就是(4-5)的n-r个解 1, 1 , 1 1 1 0 0 r r r b b  + +   −        −   =              ， 1, 2 , 2 2 0 1 0 r r r b b  + +   −        −   =              ， 1, , 0 0 1 n r n n r b b  −   −        −   =             

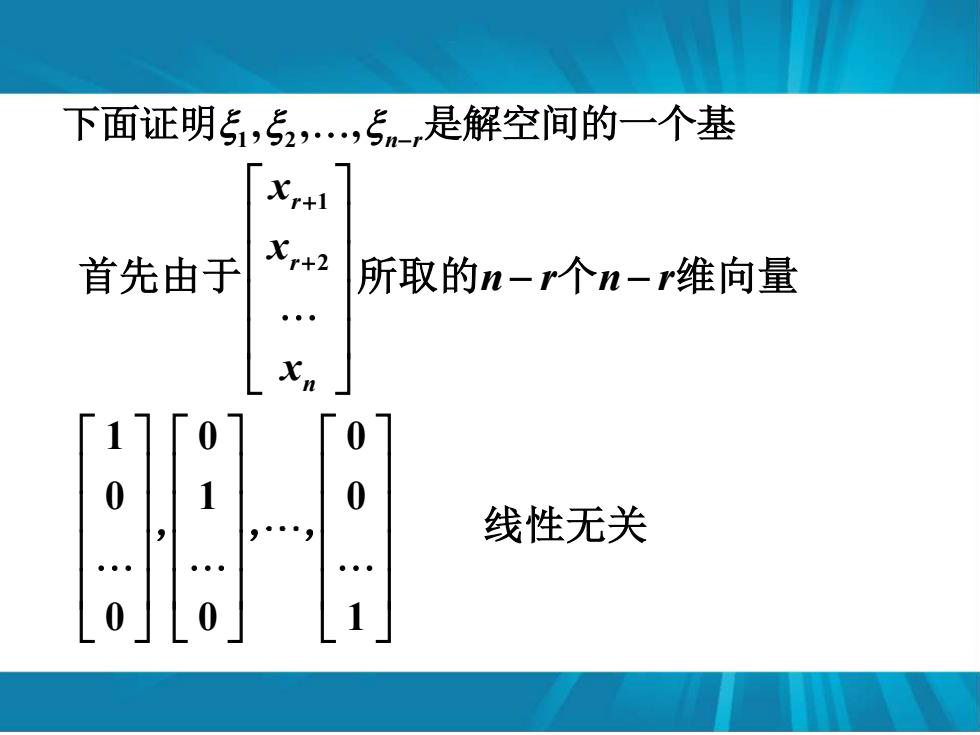
下面证明5,52，5m,是解空间的一个基 + 首先由于 Xr+2 所取的n-r个n-r维向量 七n 0 0 0 1 0 线性无关

1 2 , , , n r    下面证明  − 是解空间的一个基 1 2 1 0 0 0 1 0 0 0 1 r r n x x n r n r x + +       − −                                               首先由于 所取的 个 维向量 ， ， ， 线性无关