
第一章集合与常用逻辑用语 .2是关于x的方程x2一5x十m=0的一个根 又B={xlx2+n.x+12=0}, m=6,且A={2,3}, 3一定是关于x的方程x2十nx十12=0的一 .CA={1,4,5. 个根, (CA)UB={1,3,4,5}, n=-7,且B={3,4}, .3∈B. ∴,m十n=-1. 课后 ·训练提升 基础·巩固 6.设S={1,2,3,4},且M={x∈S|x2-5x+p=0.若 CsM={1,4},则p= 1.若全集U={0,1,2,3},且CA={2},则集合A的真子集 解析S={1,2,3,4},CsM={1,4}, 共有( ) M={2,3},即2,3是方程x2-5x十p=0的两根, A.3个 B.5个 C.7个 D.8个 .p=2X3=6. 解析由题意,得A={0,1,3},故A的真子集有2一1= 答案6 7(个. 7.设全集U=R,集合A={xlx≥0},B={yly≥1},则CA 答案C 与CB的包含关系是 2.已知全集U=R,集合A={-1,0, 解析CA={xlx<O},CB={yly<I}={x|x<1}. 1},B={x|x2-2x=0},则图中的阴 B 故CA车CB(或CA二wB). 影部分表示的集合为( ) A.{-1} B.{2} 答案CA车CB(或CA二CB) C.1,2} D.{0,2} 8.设M,P是两个非空集合,定义M与P的差集为:M一P= 解析由已知,得B={0,2. {x|x∈M,且x任P},则集合M一(M一P)= 图中阴影部分对应的集合为B∩(CA)={0,2}∩ 解析根据定义“x∈M,且x任P”等价于“x∈M∩ {x|x≠-1,且x≠0,且x≠1}={2} (C,P)” 答案B 为此引入全集U,则M一P=M∩(CP). 于是有M-(M-P)=M-[M∩(CP)]=M∩ 3.已知全集U={x|-1<x<9},A={xl1<x<a},A是U 的子集.若A≠②,则a的取值范围是() (Co[MN(GP)]=Mn((CM)U[Go(GP))=MN A.a<9B.a≤9C.a≥9D.1<a≤9 [(GMUP]=[Mn(CM]U(MNP)=U(MNP)= M∩P.(如图) 解析由题意知,集合A≠⑦,所以a>1. 又A是U的子集, 所以1<a≤9. M-P M-(M+P) 答案D 4.如图,I是全集,M,P,S是I的3个子集,则阴影部分所 答案M∩P 表示的集合是( 9.设U=R,已知集合A={x|-5<x<5},B={x0≤x<7}, 求:(1)A∩B;(2)AUB:(3)AU(CB): (4)Bn(CA);(5)(CA)∩(CB). 解如图①. (1)A∩B={xl0x<5}. A.(M∩P)∩S B.(MNP)US (2)AUB={x|-5<x<71. C.(MOP)n(LS) D.(MNP)U(CS) B A☐CB 解析阴影部分既在M内又在P内,但在S外,故选C 图① 图② 答案C (3)如图② 5.已知集合A={x|x<a},B={x|1<x<2},且AU (CRB)=R,则实数a的取值范围是() CB={x|x<0或x≥7}, .AU(CB)={xlx<5或x≥7. A.{ala≤l}B.{ala<1}C.{ala≥2}D.{ala>2} (4)如图③. 解析C.B={xlx≤1或x≥2,又AU(CRB)=R, C a≥2 答案C 图③ 21
第一章 集合与常用逻辑用语 ∴2是关于x 的方程x2-5x+m=0的一个根, ∴m=6,且A={2,3}, ∴∁UA={1,4,5}. ∵(∁UA)∪B={1,3,4,5}, ∴3∈B. 又B={x|x2+nx+12=0}, ∴3一定是关于x 的方程x2 +nx+12=0的一 个根, ∴n=-7,且B={3,4}, ∴m+n=-1. 课后 ·训练提升 基础 巩固 1.若全集U={0,1,2,3},且∁UA={2},则集合A 的真子集 共有( ) A.3个 B.5个 C.7个 D.8个 解析 由题意,得A={0,1,3},故A 的真子集有23-1= 7(个). 答案 C 2.已知全集U=R,集合 A={-1,0, 1},B={x|x2-2x=0},则图中的阴 影部分表示的集合为( ) A.{-1} B.{2} C.{1,2} D.{0,2} 解析 由已知,得B={0,2}. 图中阴影部分对应的集合为B∩(∁UA)={0,2}∩ {x|x≠-1,且x≠0,且x≠1}={2}. 答案 B 3.已知全集U={x|-1<x<9},A={x|1<x<a},A 是U 的子集.若A≠⌀,则a的取值范围是( ) A.a<9 B.a≤9 C.a≥9 D.1<a≤9 解析 由题意知,集合A≠⌀,所以a>1. 又A 是U 的子集, 所以1<a≤9. 答案 D 4.如图,I是全集,M,P,S 是I的3个子集,则阴影部分所 表示的集合是( ) A.(M∩P)∩S B.(M∩P)∪S C.(M∩P)∩(∁IS) D.(M∩P)∪(∁IS) 解析 阴影部分既在M 内又在P 内,但在S 外,故选C. 答案 C 5.已知集合 A={x|x<a},B={x|1<x<2},且 A∪ (∁RB)=R,则实数a的取值范围是( ) A.{a|a≤1}B.{a|a<1}C.{a|a≥2}D.{a|a>2} 解析 ∵∁RB={x|x≤1或x≥2},又A∪(∁RB)=R, ∴a≥2. 答案 C 6.设S={1,2,3,4},且 M ={x∈S|x2-5x+p=0}.若 ∁SM={1,4},则p= . 解析 ∵S={1,2,3,4},∁SM={1,4}, ∴M={2,3},即2,3是方程x2-5x+p=0的两根, ∴p=2×3=6. 答案 6 7.设全集U=R,集合A={x|x≥0},B={y|y≥1},则∁UA 与∁UB 的包含关系是 . 解析 ∁UA={x|x<0},∁UB={y|y<1}={x|x<1}. 故∁UA⫋∁UB(或∁UA⊆∁UB). 答案 ∁UA⫋∁UB(或∁UA⊆∁UB) 8.设M,P 是两个非空集合,定义M 与P 的差集为:M-P= {x|x∈M,且x∉P},则集合M-(M-P)= . 解析 根据定义 “x∈M,且 x∉P”等价于 “x∈M ∩ (∁UP)”. 为此引入全集U,则M-P=M∩(∁UP). 于是有M-(M -P)=M -[M ∩(∁UP)]=M ∩ {∁U[M∩(∁UP)]}=M∩{(∁UM)∪[∁U(∁UP)]}=M∩ [(∁UM)∪P]=[M∩(∁UM)]∪(M∩P)=⌀∪(M∩P)= M∩P.(如图) 答案 M∩P 9.设U=R,已知集合A={x|-5<x<5},B={x|0≤x<7}, 求:(1)A∩B;(2)A∪B;(3)A∪(∁UB); (4)B∩(∁UA);(5)(∁UA)∩(∁UB). 解 如图①. (1)A∩B={x|0≤x<5}. (2)A∪B={x|-5<x<7}. 图① 图② (3)如图②. ∁UB={x|x<0或x≥7}, ∴A∪(∁UB)={x|x<5或x≥7}. (4)如图③. 图③ 21
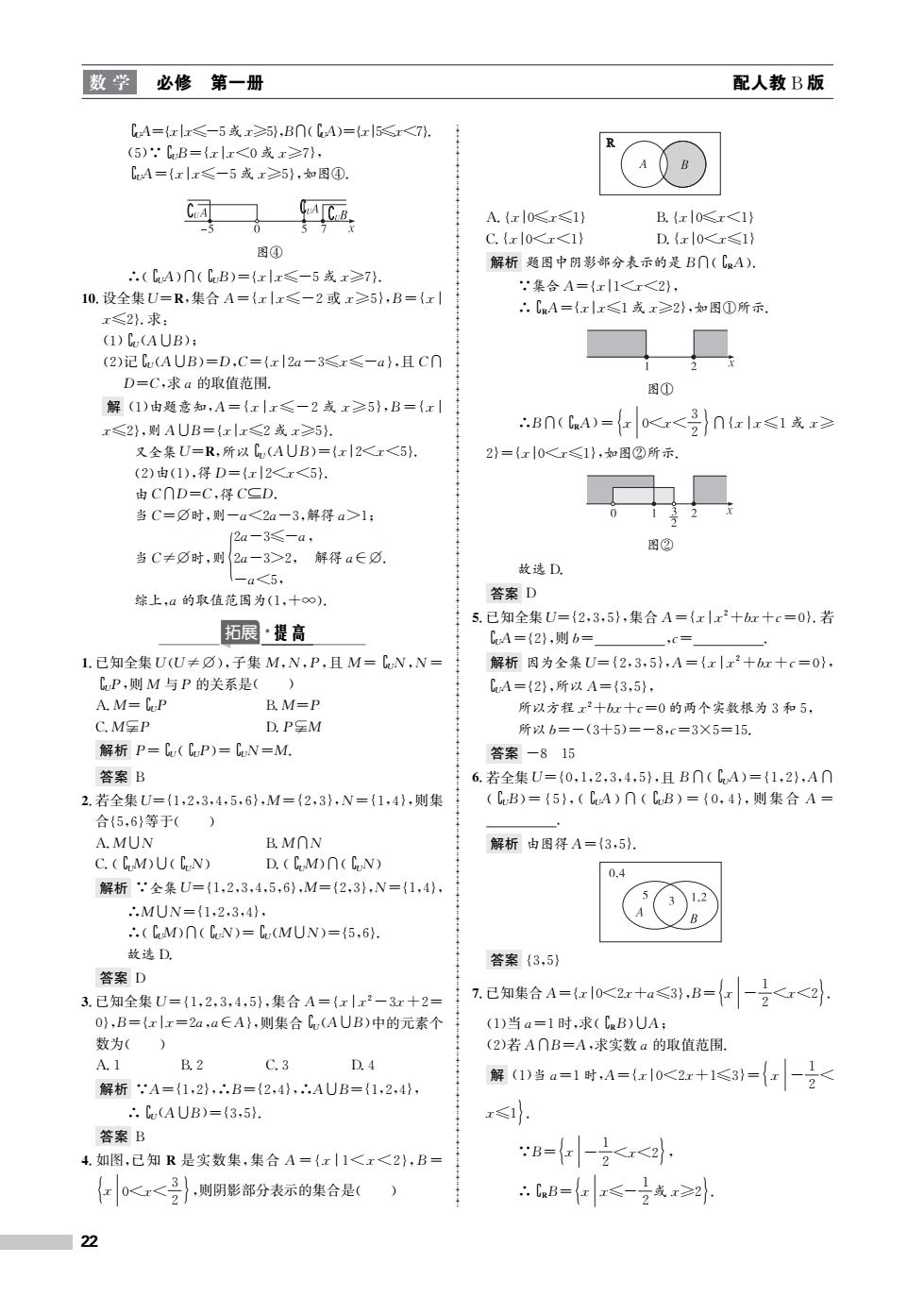
数学 必修第一册 配人教B版 CA={xlx≤-5或x≥},B∩(CA)={xl5≤x<7. (5):CB={xlx<0或x≥7}, CA={xlx≤-5或x≥5},如图④. B A.{xl0x≤1} B.{x|0x<1} C.{x|0x1} D.{x|0<x≤1} 图① 解析题图中阴影部分表示的是B∩(CRA). .(CA)∩(CB)={xlx≤-5或x≥7}. :集合A={x1<x<2}, 10.设全集U=R,集合A={x|x≤-2或x≥5},B={x| .CRA={x|x≤1或x≥2},如图①所示. x≤2}.求: (1)C(AUB); (2)记Cu(AUB)=D,C={x|2a-3≤x≤-a},且C∩ D=C,求a的取值范围. 图① 解(1)由题意知,A={xlx≤-2或x≥5},B={xl x≤2),则AUB={x|x≤2或x≥5}. :Bn(A)=0K<号}ntzl<1或r≥ 又全集U=R,所以C(AUB)={x|2<x<5. 2}={x|0<x≤1},如图②所示. (2)由(1),得D={x|2<x<5}. 由CnD=C,得C二D. 当C=☑时,则-a<2a-3,解得a>l; 12a-3-a, 图② 当C≠⑦时,则{2a一3>2, 解得a∈⑦. 故选D. -a5, 综上,a的取值范围为(1,十∞). 答案D 5.已知全集U={2,3,5},集合A={x|x2+bx十c=0}.若 拓展·提高 CA={2},则b= -C= 1.已知全集U(U≠),子集M,N,P,且M=CN,N= 解析因为全集U={2,3,5},A={x|x2+bx十c=0}, CP,则M与P的关系是() CA={2},所以A={3,5}, A.M=CoP B.M=P 所以方程x2十br十c=0的两个实数根为3和5, C.MSP D.PSM 所以b=-(3十5)=-8,c=3×5=15. 解析P=Cu(CvP)=CwN=M, 答案-815 答案B 6.若全集U={0,1,2,3,4,5},且B∩(CA)={1,2},A∩ 2.若全集U={1,2,3,4,5,6},M={2,3},N={1,4},则集 (CB)={5},(CA)∩(CB)={0,4},则集合A= 合{5,6}等于() A.MUN B.MNN 解析由图得A={3,5. C.(CM)U(CN) D.(CM)∩(CN) 0.4 解析全集U={1,2,3,4,5,6},M={2,3},N={14}, .2 ∴.MUN={1,2,3,4}, ∴.(CM)∩(CN)=Cu(MUN)={5,6. 故选D 答案{3,5} 答案D 3.已知全集U={1,2,3,4,5},集合A={x|x2-3x+2= 7已知集合A=z10<2x+a<31.B=女-2<<2 0},B={xx=2a,a∈A},则集合C(AUB)中的元素个 (1)当a=1时,求(CRB)UA: 数为() (2)若A∩B=A,求实数a的取值范围. A.1 B.2 C.3 D.4 解析A={1,2},∴.B={2,4},∴AUB={1,2,4}, 解1)当a=1时,A={z0<2z+1≤3={女-2 ,.C(AUB)={3,5}. x≤1}: 答案B 4如图,已知R是实数集,集合A={x11<x<2},B =-<, {女0<x<》,则阴影部分表示的集合是() kB={e<-或≥2 22
数 学 必修 第一册 配人教B版 ∁UA={x|x≤-5或x≥5},B∩(∁UA)={x|5≤x<7}. (5)∵∁UB={x|x<0或x≥7}, ∁UA={x|x≤-5或x≥5},如图④. 图④ ∴(∁UA)∩(∁UB)={x|x≤-5或x≥7}. 10.设全集U=R,集合A={x|x≤-2或x≥5},B={x| x≤2}.求: (1)∁U(A∪B); (2)记∁U(A∪B)=D,C={x|2a-3≤x≤-a},且C∩ D=C,求a的取值范围. 解 (1)由题意知,A={x|x≤-2或x≥5},B={x| x≤2},则A∪B={x|x≤2或x≥5}. 又全集U=R,所以∁U(A∪B)={x|2<x<5}. (2)由(1),得D={x|2<x<5}. 由C∩D=C,得C⊆D. 当C=⌀时,则-a<2a-3,解得a>1; 当C≠⌀时,则 2a-3≤-a, 2a-3>2, -a<5, 解得a∈⌀. 综上,a的取值范围为(1,+∞). 拓展 提高 1.已知全集U(U ≠ ⌀),子集 M,N,P,且 M =∁UN,N = ∁UP,则M 与P 的关系是( ) A.M=∁UP B.M=P C.M⫋P D.P⫋M 解析 P=∁U(∁UP)=∁UN=M. 答案 B 2.若全集U={1,2,3,4,5,6},M={2,3},N={1,4},则集 合{5,6}等于( ) A.M∪N B.M∩N C.(∁UM)∪(∁UN) D.(∁UM)∩(∁UN) 解析 ∵全集U={1,2,3,4,5,6},M={2,3},N={1,4}, ∴M∪N={1,2,3,4}, ∴(∁UM)∩(∁UN)=∁U(M∪N)={5,6}. 故选D. 答案 D 3.已知全集U={1,2,3,4,5},集合A={x|x2-3x+2= 0},B={x|x=2a,a∈A},则集合∁U(A∪B)中的元素个 数为( ) A.1 B.2 C.3 D.4 解析 ∵A={1,2},∴B={2,4},∴A∪B={1,2,4}, ∴∁U(A∪B)={3,5}. 答案 B 4.如图,已知 R 是实数集,集合 A={x|1<x<2},B= x 0<x< 3 2 ,则阴影部分表示的集合是( ) A.{x|0≤x≤1} B.{x|0≤x<1} C.{x|0<x<1} D.{x|0<x≤1} 解析 题图中阴影部分表示的是B∩(∁RA). ∵集合A={x|1<x<2}, ∴∁RA={x|x≤1或x≥2},如图①所示. 图① ∴B∩(∁RA)= x 0<x< 3 2 ∩{x|x≤1或x≥ 2}={x|0<x≤1},如图②所示. 图② 故选D. 答案 D 5.已知全集U={2,3,5},集合A={x|x2+bx+c=0}.若 ∁UA={2},则b= ,c= . 解析 因为全集U={2,3,5},A={x|x2+bx+c=0}, ∁UA={2},所以A={3,5}, 所以方程x2+bx+c=0的两个实数根为3和5, 所以b=-(3+5)=-8,c=3×5=15. 答案 -8 15 6.若全集U={0,1,2,3,4,5},且B∩(∁UA)={1,2},A∩ (∁UB)= {5},(∁UA)∩ (∁UB)= {0,4},则 集 合 A = . 解析 由图得A={3,5}. 答案 {3,5} 7.已知集合A={x|0<2x+a≤3},B= x - 1 2 <x<2 . (1)当a=1时,求(∁RB)∪A; (2)若A∩B=A,求实数a的取值范围. 解 (1)当a=1时,A={x|0<2x+1≤3}= x - 1 2 < x≤1 . ∵B= x - 1 2 <x<2 , ∴∁RB= x x≤- 1 2 或x≥2 . 22

第一章集合与常用逻辑用语 .(CB)UA={x|x≤1或x≥2}. (2)设全集1=AUB,求(CA)U(C,B): (2)若A∩B=A,则A二B. (3)写出(CA)U(CB)的所有子集 A=iz0<2x+a≤3={z-<r<322} 解(1)因为A∩B={2},所以2×22+2a十2=0,解得 a=-5,所以A=2,B=-52. 2 解得一1<a≤1. 3a∠2 (2)因为1=-5,22,所以A=(-5,B= 2 .实数a的取值范围是{a-1<a≤l}. 号},所以(AU(B)={-5,2} 挑战·创新 (3)(0A)U(B)的所有子集为,{分}{-5, 设集合A={x|2x2+a.x十2=0},B={x|x2+3x+2a= 0},A∩B={2} -5} (1)求a的值及集合A,B: 1.2常用逻辑用语 1.2.1命题与量词 1.了解命题的概念,能判断一个语句是不是命题, 2.会判断一个命题的真假 课标定位 3.理解全称量词和存在量词 素养阐释 4.能判断全称量词命题和存在量词命题的真假, 5.体会数学抽象的过程,培养逻辑推理能力. 课前 基础认知 一、命题的概念 (2)0是0的子集: 【问题思考】 (3)x-2>5-2x. 1.你能判断下列语句的真假吗? 答案(1)是命题,是假命题.(2)是命题,且是真命题. (1)空集☑是集合{0}的真子集; (3)不是命题. (2)直角三角形中只有一个角为直角: 二、量词 (3)x>-2. 【问题思考】 提示(1)(2)能,(3)不能. 1.(1)同一圆的直径大于它的半径:(2)存在x∈Z, 2.填空:可供真假判断的陈述语句就是命题.判断为真 |x|=5.若以上命题为真命题,则其成立的条件是什么? 的语句称为真命题,判断为假的语句称为假命题.为了方便 提示(1)所有圆.(2)x=土5. 叙述,命题可以用小写英文字母表示. 2.填空:(1)一般地,“任意”“所有”“每一个”在陈述中 3.(1)数学中的“命题”和新闻报道中的“命题”一样吗? 表示所述事物的全体,称为全称量词,用符号“H”表示.含有 (2)是否存在既是真命题又是假命题的命题? 全称量词的命题,称为全称量词命题.全称量词命题就是形 提示(1)不一样.新闻报道中的“命题”是“命制的题 如“对集合M中的所有元素x,r(x)”的命题,可简记为 目”的简写,常指待研究的问题或需要完成的任务等 Hx∈M,r(x). (2)不存在.一个命题要么是真命题,要么是假命题,不 (2)“存在”“有”“至少有一个”在陈述中表示所述事物 能同时既是真命题又是假命题,也不能模棱两可、无法判断! 的个体或部分,称为存在量词,用符号“3”表示.含有存在量 是真命题还是假命题, 词的命题,称为存在量词命题.存在量词命题就是形如“存在 4.做一做:判断下列语句是否为命题,若为命题,指明 集合M中的元素x,s(x)”的命题,可简记为3x∈M, 其真假. s(x) (1)y=a.x十1,a∈R是一次函数: 3.存在量词命题和全称量词命题有哪些不同的表述? 23
第一章 集合与常用逻辑用语 ∴(∁RB)∪A={x|x≤1或x≥2}. (2)若A∩B=A,则A⊆B. ∵A={x|0<2x+a≤3}= x - a 2 <x≤ 3-a 2 , ∴ - a 2 ≥- 1 2 , 3-a 2 <2, 解得-1<a≤1, ∴实数a的取值范围是{a|-1<a≤1}. 挑战 创新 设集合A={x|2x2+ax+2=0},B={x|x2+3x+2a= 0},A∩B={2}. (1)求a的值及集合A,B; (2)设全集I=A∪B,求(∁IA)∪(∁IB); (3)写出(∁IA)∪(∁IB)的所有子集. 解 (1)因为A∩B={2},所以2×22+2a+2=0,解得 a=-5,所以A= 1 2 ,2 ,B={-5,2}. (2)因为I= -5, 1 2 ,2 ,所以∁IA={-5},∁IB= 1 2 ,所以(∁IA)∪(∁IB)= -5, 1 2 . (3)(∁IA)∪(∁IB)的所有子集为⌀, 1 2 ,{-5}, -5, 1 2 . 1.2 常用逻辑用语 1.2.1 命题与量词 课标定位 素养阐释 1.了解命题的概念,能判断一个语句是不是命题. 2.会判断一个命题的真假. 3.理解全称量词和存在量词. 4.能判断全称量词命题和存在量词命题的真假. 5.体会数学抽象的过程,培养逻辑推理能力. 课前 ·基础认知 一、命题的概念 【问题思考】 1.你能判断下列语句的真假吗? (1)空集⌀是集合{0}的真子集; (2)直角三角形中只有一个角为直角; (3)x>-2. 提示 (1)(2)能,(3)不能. 2.填空:可供真假判断的陈述语句就是命题.判断为真 的语句称为真命题,判断为假的语句称为假命题.为了方便 叙述,命题可以用小写英文字母表示. 3.(1)数学中的“命题”和新闻报道中的“命题”一样吗? (2)是否存在既是真命题又是假命题的命题? 提示 (1)不一样.新闻报道中的“命题”是“命制的题 目”的简写,常指待研究的问题或需要完成的任务等. (2)不存在.一个命题要么是真命题,要么是假命题,不 能同时既是真命题又是假命题,也不能模棱两可、无法判断 是真命题还是假命题. 4.做一做:判断下列语句是否为命题.若为命题,指明 其真假. (1)y=ax+1,a∈R是一次函数; (2)⌀是⌀的子集; (3)x-2>5-2x. 答案 (1)是命题,是假命题.(2)是命题,且是真命题. (3)不是命题. 二、量词 【问题思考】 1.(1)同一圆的直径大于它的半径;(2)存在x∈Z, |x|=5.若以上命题为真命题,则其成立的条件是什么? 提示 (1)所有圆.(2)x=±5. 2.填空:(1)一般地,“任意”“所有”“每一个”在陈述中 表示所述事物的全体,称为全称量词,用符号“∀”表示.含有 全称量词的命题,称为全称量词命题.全称量词命题就是形 如“对集合 M 中的所有元素x,r(x)”的命题,可简记为 ∀x∈M,r(x). (2)“存在”“有”“至少有一个”在陈述中表示所述事物 的个体或部分,称为存在量词,用符号“∃”表示.含有存在量 词的命题,称为存在量词命题.存在量词命题就是形如“存在 集合 M 中的元素x,s(x)”的命题,可简记为 ∃x∈M, s(x). 3.存在量词命题和全称量词命题有哪些不同的表述? 23

数学 必修 第一册 配人教B版 提示 提示(1)假命题.因为当x=0时,x2=0. 命 全称量词命题“Hx∈M, 存在量词命题“3x∈M, 题 r(x)” s(x)” ②真命题因为当a=0时,血30=宁 ①所有的x∈M,r(x) ①存在x∈M,使s(x) 2.(1)要判定全称量词命题Hx∈M,r(x)是真命题,必 成立; 成立: 须对限定集合M中的每个元素x,验证r(x)成立:但要判 ②对一切x∈M,r(x)) ②至少有一个x∈M,使 定其是假命题,却只需举出集合M中的一个元素x。,使得 表 成立: s(x)成立: r(x。)不成立即可. ③对每一个x∈M,r(.x) ③对有些x∈M,使s(x) (2)要判定存在量词命题3x∈M,s(x)是真命题,只要 成立: 成立: 法 ④任选一个x∈M,使 ④对某个x∈M,使s(x) 在限定集合M中,找到一个元素xo,使得s(xo)成立即可; r(x)成立: 成立: 但要判定其是假命题,却需要说明集合M中的每一个x,都 ⑤凡x∈M,都有r(x) ⑤有一个x∈M.使s(x) 使得s(x)不成立 成立 成立 3.做一做:下列命题为真命题的是 (填序号) 4.做一做:下列命题中,全称量词命题是 ;存 在量词命题是 (填序号) 0V>5.>3:@3x∈N,x=2:③Vx∈Zx≥ ①Hx∈R,x2≥0:②有些集合无真子集:③直角三角 -1;④3x∈(-∞,0),√x+10=100. 形的边长满足勾股定理。 答案①② 答案①③② 【思考辨析】 三、全称量词命题、存在量词命题的真假判断 判断下列说法是否正确,正确的在后面的括号内画 【问题思考】 “√”,错误的画“X” 1.试判断下列命题的真假, (1)同一个全称量词命题的表述是唯一的. (×) (1)Hx∈N,x2>0: (2)“全等三角形的面积相等”是全称量词命题.(√) (2)设A是所有角组成的集合,则3a∈A,sina= (3)“3x∈R,2x>x十1”是存在量词命题,且是假 命题 (×) 课堂 ·重难突破 【变式训练1】判断下列语句是不是命题.若是命题, 探究一命题真假的判断 指明其真假。 【例1】判断下列语句是不是命题.若是,判断其真假 (1)你是高一学生吗? 并说明理由。 (2)能被6整除的数既能被3整除,也能被2整除: (1)求证:5是无理数: (3)Hx∈Q,了x2-1是有理数: (2)并非所有的人都喜欢吃苹果; (3)若x十y和xy都是有理数,则x,y都是有理数; (4)3xy∈Z,使3x-2y=10. (4)对任意x∈R,2x2+5>0: 答案(1)不是命题,(2)(3)(4)是命题,且是真命题. (5)3xo∈R,使x+1<0. 解(1)不是陈述句,不是命题, 探究二 全称量词命题、存在量词命题的判断 (2)是真命题.有的人喜欢吃革果,有的人不喜欢吃苹果」 【例2】判断下列命题是全称量词命题还是存在量词 (3)是假命题.如√3十(一√5)和√5×(一√)都是有理 命题 数,但和一5都是无理数 (1)至少有一个整数,它既能被2整除,又能被5整除: (4)是真命题, (2)Hx∈{xx是无理数},x2是无理数: 2x2≥0,.2x2+5>0. (3)负数的平方是正数: (5)是假命题. x≥0,∴x十1>0,即无论x0取何值,x6十1均不 (4)有的实数是无限不循环小数. 可能小于0 分析找堂词判断 ①反思感悟 解(1)中含有存在量词“至少有一个”,所以是存在量 1.判定一个全称量词命题是真命题,一般需要经 词命题. 过严格的推理论证,在判断时,要有推理依据,有时应 (2)中含有全称量词符号“H”,所以是全称量词命题. 综合各种情况作出正确的判断. (3)中省略了全称量词“所有的”,所以是全称量词 2.判定一个全称量词命题为假命题,只需要举出 命题 一个反例即可 (4)中含有存在量词“有的”,所以是存在量词命题 24
数 学 必修 第一册 配人教B版 提示 命 题 全称量词命题“∀x∈M, r(x)” 存在 量 词 命 题 “∃x∈M, s(x)” 表 述 方 法 ①所有的 x∈M,r(x) 成立; ②对一切 x∈M,r(x) 成立; ③对每一个x∈M,r(x) 成立; ④ 任 选 一 个 x∈M,使 r(x)成立; ⑤凡x∈M,都有r(x) 成立 ① 存 在 x ∈ M,使s(x) 成立; ②至 少 有 一 个 x∈M,使 s(x)成立; ③对有些x∈M,使s(x) 成立; ④对某个x∈M,使s(x) 成立; ⑤有一个x∈M,使s(x) 成立 4.做一做:下列命题中,全称量词命题是 ;存 在量词命题是 .(填序号) ①∀x∈R,x2≥0;②有些集合无真子集;③直角三角 形的边长满足勾股定理. 答案 ①③ ② 三、全称量词命题、存在量词命题的真假判断 【问题思考】 1.试判断下列命题的真假. (1)∀x∈N,x2>0; (2)设A 是所有角组成的集合,则∃α∈A,sinα= 1 2 . 提示 (1)假命题.因为当x=0时,x2=0. (2)真命题.因为当α=30°时,sin30°= 1 2 . 2.(1)要判定全称量词命题∀x∈M,r(x)是真命题,必 须对限定集合 M 中的每个元素x,验证r(x)成立;但要判 定其是假命题,却只需举出集合 M 中的一个元素x0,使得 r(x0)不成立即可. (2)要判定存在量词命题∃x∈M,s(x)是真命题,只要 在限定集合 M 中,找到一个元素x0,使得s(x0)成立即可; 但要判定其是假命题,却需要说明集合 M 中的每一个x,都 使得s(x)不成立. 3.做一做:下列命题为真命题的是 .(填序号) ①∀x>5,x>3;②∃x∈N,x= 1 x ;③∀x∈Z,x≥ -1;④∃x∈(-∞,0), x+10=100. 答案 ①② 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画 “√”,错误的画“×”. (1)同一个全称量词命题的表述是唯一的. (×) (2)“全等三角形的面积相等”是全称量词命题. (√) (3)“∃x∈R,2x>x+1”是存在量词命题,且是假 命题. (×) 课堂 ·重难突破 探究一 命题真假的判断 【例1】判断下列语句是不是命题.若是,判断其真假 并说明理由. (1)求证:3是无理数; (2)并非所有的人都喜欢吃苹果; (3)若x+y和xy都是有理数,则x,y都是有理数; (4)对任意x∈R,2x2+5>0; (5)∃x0∈R,使x 2 0+1<0. 解 (1)不是陈述句,不是命题. (2)是真命题.有的人喜欢吃苹果,有的人不喜欢吃苹果. (3)是假命题.如 3+(- 3)和 3×(- 3)都是有理 数,但 3和- 3都是无理数. (4)是真命题. ∵2x2≥0,∴2x2+5>0. (5)是假命题. ∵x 2 0≥0,∴x 2 0+1>0,即无论x0 取何值,x 2 0+1均不 可能小于0. 1.判定一个全称量词命题是真命题,一般需要经 过严格的推理论证,在判断时,要有推理依据,有时应 综合各种情况作出正确的判断. 2.判定一个全称量词命题为假命题,只需要举出 一个反例即可. 【变式训练1】判断下列语句是不是命题.若是命题, 指明其真假. (1)你是高一学生吗? (2)能被6整除的数既能被3整除,也能被2整除; (3)∀x∈Q, 1 3 x2-1是有理数; (4)∃x,y∈Z,使3x-2y=10. 答案 (1)不是命题,(2)(3)(4)是命题,且是真命题. 探究二 全称量词命题、存在量词命题的判断 【例2】判断下列命题是全称量词命题还是存在量词 命题. (1)至少有一个整数,它既能被2整除,又能被5整除; (2)∀x∈{x|x 是无理数},x2 是无理数; (3)负数的平方是正数; (4)有的实数是无限不循环小数. 分析 找量词 → 判断 解 (1)中含有存在量词“至少有一个”,所以是存在量 词命题. (2)中含有全称量词符号“∀”,所以是全称量词命题. (3)中省略了全称量词“所有的”,所以是全称量词 命题. (4)中含有存在量词“有的”,所以是存在量词命题. 24

第一章集合与常用逻辑用语 ①反思感悟 判断一个语句是全称量词命题还是存在量词命题 易错辨析 时,要注意以下三点: 因对符号“V”了”理解不透致错 (1)首先判断该语句是不是一个命题 【典例】已知命题“Vx1∈[-1,1],3x2∈[0,2],x≤ (2)对命题属性进行判定时,关键是看命题中含有 x2十2m”为真命题,求实数m的取值范围 的量词是全称量词还是存在量词 错解令y=x2,x∈[-1,1],y=-x十2m,x∈[0,2]. (3)对于省略了量词的命题,要根据命题所涉及的 由图象(图象略)可知,y=一x十2m的最小值ym= 实际意义进行判断, -2+2m,y=x2的最大值y=12=1,则-2+2m>1,解 【变式训练2】判断下列命题是全称量词命题还是存 3 得m>2 在量词命题。 以上解答过程中都有哪些错误?出错的原因是什么? (1)等边三角形的三边相等; 你如何改正?你如何防范? (2)存在实数x,使x3-3>0. 提示上面错误的地方是应求y=-x十2m,x∈[0,2] 答案(1)是全称量词命题, 的最大值」 (2)是存在量词命题, 正解令y=x2,x∈[-1,1],y=-x+2m,x∈[0, 探究三全称量词命题、存在量词命题的应用 2],结合图象(图象略)可得,y=x2,x∈[一1,1]的最大值为 ymx=(-1)2=12=1, 【例3】若命题“x∈[-3,2],a十2x+1>0”为真命 y=-x十2m,x∈[0,2]的最大值为y=2m. 题,求实数a的取值范围. 解,Hx∈[-3,2],a十2x十1>0为真命题, 由命题为真命题,得2m≥1,解得m≥2 ∴对Hx∈[-3,2],a十2x+1>0恒成立, 故m的取值范围是 2+) 即对Hx∈[-3,2],a>-(2x十1)恒成立. ①防范措施 令y=一2x一1,由图象(图象略)可知,ymx=一2X 1.弄清符号“H”和“了”的含义。 (-3)-1=5,.a>5. 2.将问题转化为最值时,弄清求甲的最大(小)值 故a的取值范围是(5,十∞). 后,应求乙的最大值还是最小值 延伸探究 已知命题“Ha∈[一3,2],a+2x+1>0”为真命题,求 随堂训练 实数x的取值范围. 1.下列命题是真命题的是( 解由题意,得a>-2x-l,a∈[-3,2]恒成立, A.一2020不是偶数 ,a能取的最小值为一3, B.任何实数的平方都是非负数 .-2x-1<一3,解得x>1. C,y=kx(k∈R)是正比例函数 x的取值范固是(1,十∞). D.无理数的平方是有理数 飞反思感悟 借助全称量词命题的有关知识求式子中某个参数 答案B 的取值范围的问题为恒成立问题 2.己知下列语句:①上海世博会中国国家馆真宏伟啊!②甲 型H1N1流感是怎样传播的?③2是个很小的数; 借助存在量词命题的有关知识求式子中某个参数 的取值范围的问题为存在性问题,这类问题一般要先 ④不等式x-3>0的解是x>3:⑤2010年6月11日是世 对结论作出存在性的假设,再由此假设出发,结合已知 界杯开幕的日子. 条件进行推理论证.若推出合理结论,则可肯定假设: 其中是命题的个数是( 若导出矛盾,则可否定假设 A.1 B.2 C.3 D.4 【变式训练3】已知命题“3x∈[-3,2],3a十x-2= 解析④⑤是命题. 0”为真命题,求实数a的取值范围. 答案B 解由3a十x-2=0,得3a-2=-x. 3.下列命题中的真命题是 .(填序号) x∈[-3,2] ①存在一个x∈Z,使得3x十4=5: -2≤-x≤3. ②x2-y2=(x-y)(x十y): :.-2≤3a-2≤3,解得0≤a≤3 ③所有整数只有两个因数: ④正方形的对角线相等。 故实款口的取值范网是0,】, 11 解析由3x十4=5,得x= 3,3任乙,故①是假命题: 25
第一章 集合与常用逻辑用语 判断一个语句是全称量词命题还是存在量词命题 时,要注意以下三点: (1)首先判断该语句是不是一个命题. (2)对命题属性进行判定时,关键是看命题中含有 的量词是全称量词还是存在量词. (3)对于省略了量词的命题,要根据命题所涉及的 实际意义进行判断. 【变式训练2】判断下列命题是全称量词命题还是存 在量词命题. (1)等边三角形的三边相等; (2)存在实数x,使x3-3>0. 答案 (1)是全称量词命题, (2)是存在量词命题. 探究三 全称量词命题、存在量词命题的应用 【例3】若命题“∀x∈[-3,2],a+2x+1>0”为真命 题,求实数a的取值范围. 解 ∵∀x∈[-3,2],a+2x+1>0为真命题, ∴对∀x∈[-3,2],a+2x+1>0恒成立, 即对∀x∈[-3,2],a>-(2x+1)恒成立. 令y=-2x-1,由图象(图象略)可知,ymax=-2× (-3)-1=5,∴a>5. 故a的取值范围是(5,+∞). 已知命题“∀a∈[-3,2],a+2x+1>0”为真命题,求 实数x 的取值范围. 解 由题意,得a>-2x-1,a∈[-3,2]恒成立. ∵a能取的最小值为-3, ∴-2x-1<-3,解得x>1. ∴x 的取值范围是(1,+∞). 借助全称量词命题的有关知识求式子中某个参数 的取值范围的问题为恒成立问题. 借助存在量词命题的有关知识求式子中某个参数 的取值范围的问题为存在性问题,这类问题一般要先 对结论作出存在性的假设,再由此假设出发,结合已知 条件进行推理论证.若推出合理结论,则可肯定假设; 若导出矛盾,则可否定假设. 【变式训练3】已知命题“∃x∈[-3,2],3a+x-2= 0”为真命题,求实数a的取值范围. 解 由3a+x-2=0,得3a-2=-x. ∵x∈[-3,2], ∴-2≤-x≤3. ∴-2≤3a-2≤3,解得0≤a≤ 5 3 . 故实数a的取值范围是 0, 5 3 . 易 错 辨 析 因对符号“∀”“∃”理解不透致错 【典例】已知命题“∀x1∈[-1,1],∃x2∈[0,2],x 2 1≤ -x2+2m”为真命题,求实数m 的取值范围. 错解 令y=x2,x∈[-1,1],y=-x+2m,x∈[0,2]. 由图象(图象略)可知,y=-x+2m 的最小值ymin= -2+2m,y=x2 的最大值ymax=12=1,则-2+2m>1,解 得m> 3 2 . 以上解答过程中都有哪些错误? 出错的原因是什么? 你如何改正? 你如何防范? 提示 上面错误的地方是应求y=-x+2m,x∈[0,2] 的最大值. 正解 令y=x2,x∈[-1,1],y=-x+2m,x∈[0, 2],结合图象(图象略)可得,y=x2,x∈[-1,1]的最大值为 ymax=(-1)2=12=1, y=-x+2m,x∈[0,2]的最大值为ymax=2m. 由命题为真命题,得2m≥1,解得m≥ 1 2 . 故m 的取值范围是 1 2 ,+∞ . 1.弄清符号“∀”和“∃”的含义. 2.将问题转化为最值时,弄清求甲的最大(小)值 后,应求乙的最大值还是最小值. 随堂训练 1.下列命题是真命题的是( ) A.-2020不是偶数 B.任何实数的平方都是非负数 C.y=kx(k∈R)是正比例函数 D.无理数的平方是有理数 答案 B 2.已知下列语句:①上海世博会中国国家馆真宏伟啊! ②甲 型 H1N1流感是怎样传播的? ③2-100 是个很小的数; ④不等式x-3>0的解是x>3;⑤2010年6月11日是世 界杯开幕的日子. 其中是命题的个数是( ) A.1 B.2 C.3 D.4 解析 ④⑤是命题. 答案 B 3.下列命题中的真命题是 .(填序号) ①存在一个x∈Z,使得3x+4=5; ②x2-y 2=(x-y)(x+y); ③所有整数只有两个因数; ④正方形的对角线相等. 解析 由3x+4=5,得x= 1 3 , 1 3 ∉Z,故①是假命题; 25