第二章电感电容压控振荡器 w2 1 R,C Woa C,+C2 (2.15) R,CC2 由此,闭环传递函数可以表示为: NHo()= NK'(s+w) H=1+HoR) (2.16) S3+Wp2S2+K's+K'W> 其中K为环路增益: K=Kvco (2.17 2TTNC2 由此可见,频率综合器的开环传递函数与调谐增益成正比,调谐增益直接影 响到频率综合器的开环增益和闭环时的稳定性。同时,调谐增益也会影响相位噪 声性能,调谐增益越大,压控电压上相同幅度的电压噪声引起的频率变化也越大, 锁相环环路对噪声越敏感,相位噪声性能就会越差。 cp 2T ZFe) Kyco PFD+CP Loop 中ot6) Filter VCO 中avg=中ousN Divider N 图2.5三阶频率综合器的s域线性模型 icp VCTRL R1 图2.6二阶无源滤波器
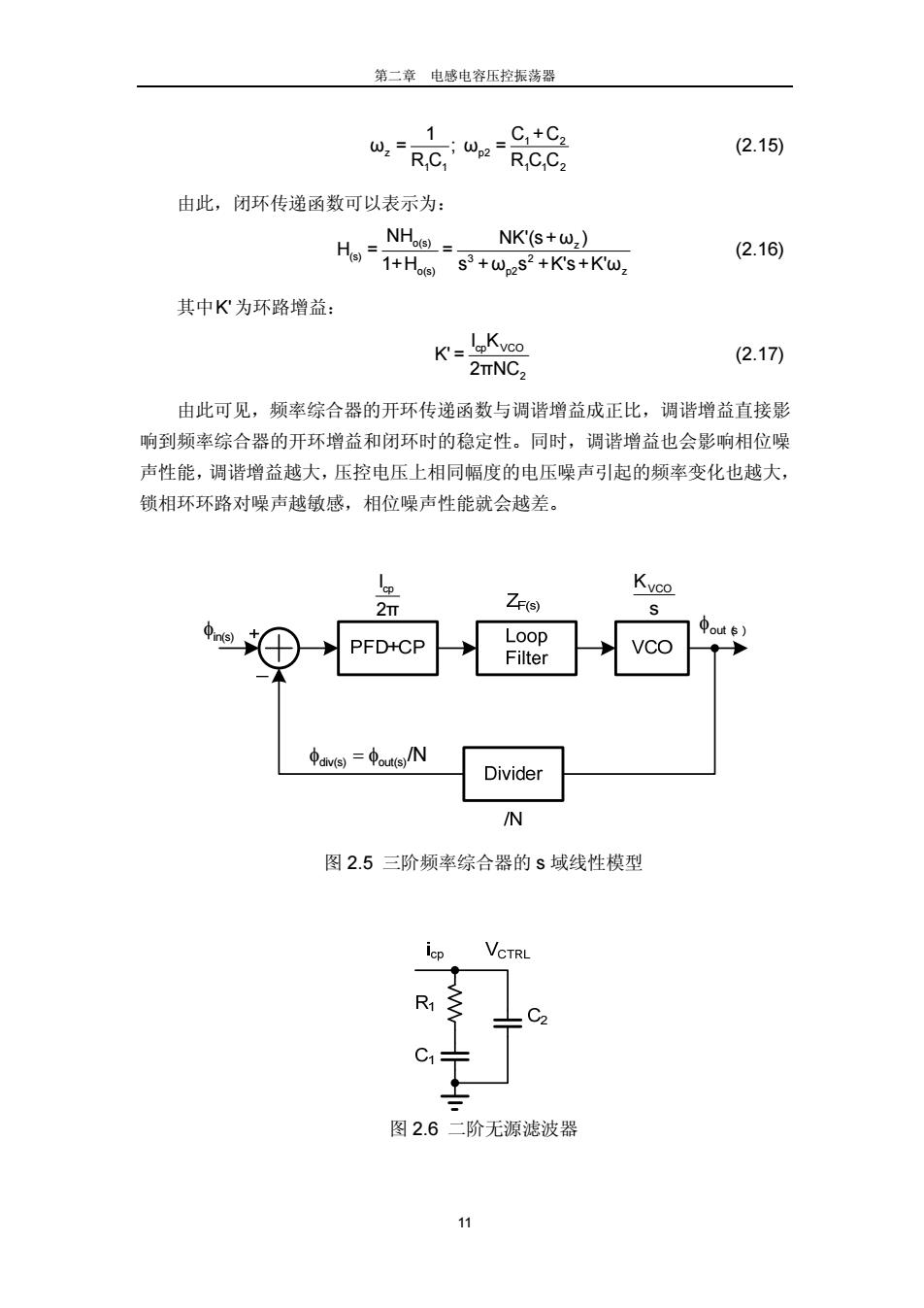
第二章 电感电容压控振荡器 11 1 2 z p2 11 112 1 C +C ω = ; ω = RC RCC (2.15) 由此,闭环传递函数可以表示为: o(s) z (s) 3 2 o(s) p2 z NH NK'(s+ω ) H= = 1+H s +ω s +K's+K'ω (2.16) 其中K'为环路增益: cp VCO 2 I K K' = 2πNC (2.17) 由此可见,频率综合器的开环传递函数与调谐增益成正比,调谐增益直接影 响到频率综合器的开环增益和闭环时的稳定性。同时,调谐增益也会影响相位噪 声性能,调谐增益越大,压控电压上相同幅度的电压噪声引起的频率变化也越大, 锁相环环路对噪声越敏感,相位噪声性能就会越差。 φ =φ div(s) out(s)/N φin(s) cp I 2π V C O K s φ o u ︵t s ︶ 图 2.5 三阶频率综合器的 s 域线性模型 图 2.6 二阶无源滤波器

第二章电感电容压控振荡器 参考文献 [1]唐长文,“电感电容压控振荡器”,博士学位论文,2004年4月 [2]A,Hajimiri and T.H.Lee,"Design issues in CMOS differential LC oscillators,"IEEE J.Solid-State Circuits,vol.34,pp.717-214,May 1999. [3]D.B.Leeson,"A simple model of feedback oscillator noises spectrum,"Proc. IEEE,vol.54,pp.329-330,Feb.1966 [4]J.Craninckx and M.Steyaert,"Low-noise voltage-controlled oscillators using enhanced LC-tanks,"IEEE Trans.Circuits Syst.Il,vol.42,pp. 794904,Dec.1995. [5]B.Razavi,"A study of phase noise in CMOS oscillators,"EEE J. Solid-State Circuits,vol.31,pp.331-343,Mar.1996. [6]C.Samor,A.L.Lacaita,F.Villa,and F.Zappa,"Spectrum folding and phase noise in LC tuned oscillators,"IEEE Trans.Circuits Syst.Il,vol.45,pp 781-790,Jul.1995. [7]A.Hajimiri and T.H.Lee,"A general theory of phase noise in electrical oscillators,"IEEE J.Solid-State Circuits,vol.33,pp.179-194,Feb.1998. [8]T.H.Lee and A.Hajimiri,"Oscillator phase noise:A tutorial,"IEEE J. Solid-State Circuits,vol.35,pp.326-336,Mar.2000. [9]Hoon Hee Chung,Wenjian Chen,Bertan Bakkaloglu,Hugh J.Barnaby, Bert Vermeire,and Sayfe Kiaei,"Analysis of single events effects on monolithic PLL frequency synthesizers,"IEEE Transactions ON NUCLEAR SCIENCE,vol.53,no.6,Dec.2006. [101.何捷,“DVB-T接收机中频率综合器的研究”,博士学位论文,2005年4 月20日 12
第二章 电感电容压控振荡器 12 参考文献 [1] 唐长文,“电感电容压控振荡器”,博士学位论文,2004 年 4 月 [2] A, Hajimiri and T.H. Lee, “Design issues in CMOS differential LC oscillators,” IEEE J.Solid-State Circuits, vol. 34, pp. 717-214, May 1999. [3] D.B. Leeson, “A simple model of feedback oscillator noises spectrum,” Proc. IEEE, vol. 54, pp. 329-330, Feb. 1966. [4] J. Craninckx and M. Steyaert, “Low-noise voltage-controlled oscillators using enhanced LC-tanks,” IEEE Trans. Circuits Syst. II, vol. 42, pp. 794_904, Dec. 1995. [5] B. Razavi, “A study of phase noise in CMOS oscillators,” IEEE J. Solid-State Circuits, vol. 31, pp. 331-343, Mar. 1996. [6] C. Samor, A. L. Lacaita, F. Villa, and F. Zappa, “Spectrum folding and phase noise in LC tuned oscillators,” IEEE Trans. Circuits Syst. II, vol. 45, pp. 781-790, Jul. 1995. [7] A. Hajimiri and T. H. Lee, “A general theory of phase noise in electrical oscillators,” IEEE J. Solid-State Circuits, vol. 33, pp. 179-194, Feb. 1998. [8] T. H. Lee and A. Hajimiri, “Oscillator phase noise: A tutorial,” IEEE J. Solid-State Circuits, vol. 35, pp. 326-336, Mar. 2000. [9] Hoon Hee Chung, Wenjian Chen, Bertan Bakkaloglu, Hugh J. Barnaby, Bert Vermeire, and Sayfe Kiaei, “Analysis of single events effects on monolithic PLL frequency synthesizers,” IEEE Transactions ON NUCLEAR SCIENCE, vol. 53, no. 6, Dec. 2006. [10].何捷,“DVB-T 接收机中频率综合器的研究”,博士学位论文,2005 年 4 月 20 日
第三章宽带压控振荡器的设计与优化 第三章宽带压控振荡器的设计与优化 随着系统集成度的提高,越来越多的系统要求振荡器能够提供更宽的频率范 围,输出频率对压控振荡器的性能影响变得日益明显。本章主要介绍了输出频率 对压控振荡器各性能的影响,进而分析了宽带压控振荡器设计中需要注意的问 题。 3.1片上电感的优化 Start-up Start-up Tank amplitude Tank amplitude tr1 tr1 tr2 tr2 W(um) W(um) (a) (b) 图3.1()设计约束的图形表示(b)频率范围加宽后的设计约束 根据第二章中的介绍,对于电感电容压控振荡器,其输出频率只和电感电容 值有关。由于在确定可变电容类型的情况下,可变电容的最大值和最小值的比值 是一定的。因此设计电感电容压控振荡器时需要考虑的独立变量最后可以归结到 功耗、电感几何参数(决定电感的感值大小L0和芯片面积)、可变电容最大值 Cmax(根据可变电容特性可确定其最小值Cmin)和差分对管的宽度W(决定等效负 阻大小。为了减小寄生电容和噪声,差分对管的长度L一般设为最小长度)这几个 参数。根据振荡器的性能指标,对于输出频率,其输出频率覆盖范围必须包含所 需频率范围,根据式(2.1)有: >w2a LoCmin (3.1) 1w2m LoCmax (3.2) wmax与wmn分别为频率范围要求的最高与最低频率。对于起振条件,振荡 13
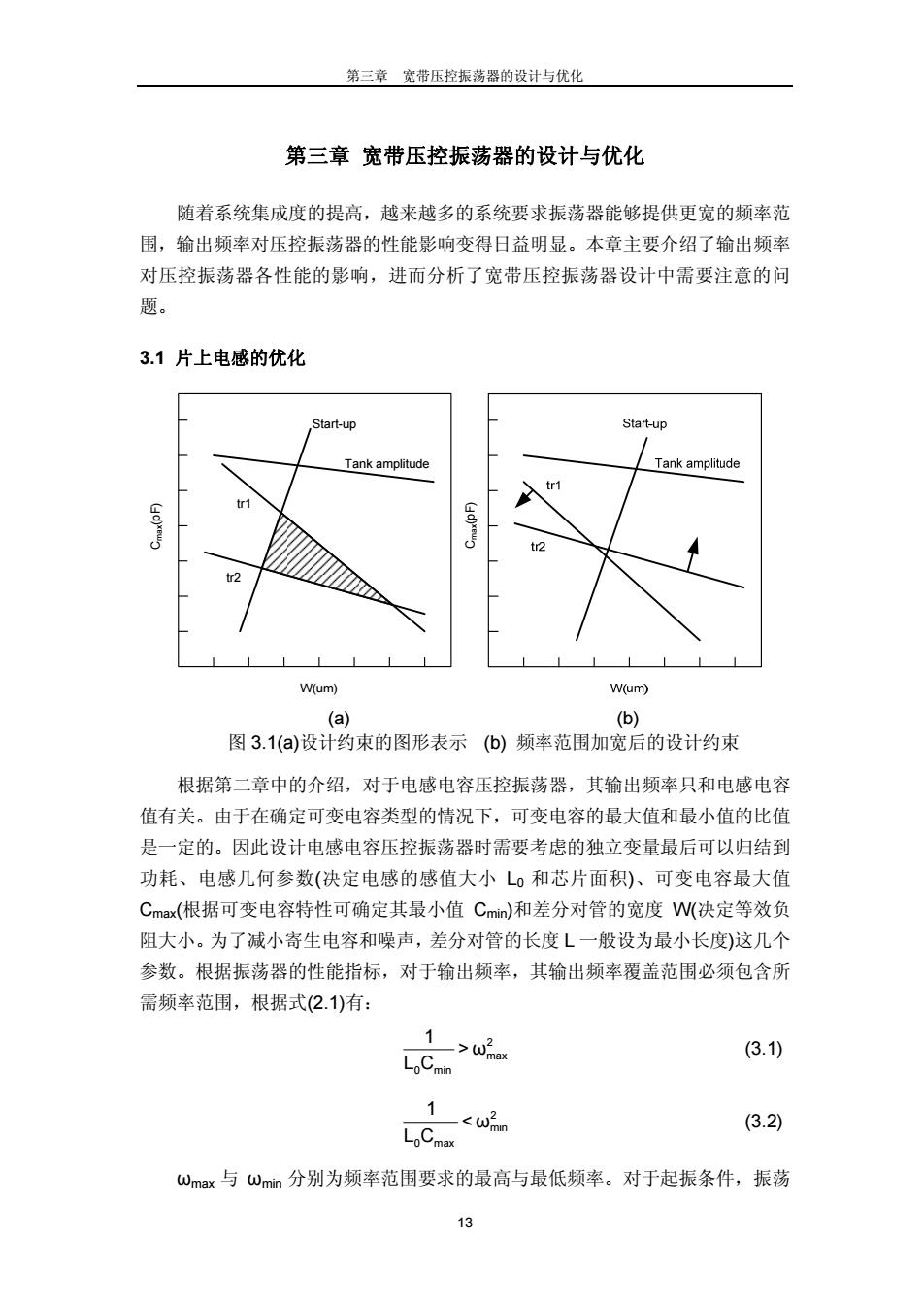
第三章 宽带压控振荡器的设计与优化 13 第三章 宽带压控振荡器的设计与优化 随着系统集成度的提高,越来越多的系统要求振荡器能够提供更宽的频率范 围,输出频率对压控振荡器的性能影响变得日益明显。本章主要介绍了输出频率 对压控振荡器各性能的影响,进而分析了宽带压控振荡器设计中需要注意的问 题。 3.1 片上电感的优化 Cmax(pF) W(um) tr1 tr2 Start-up Tank amplitude Cmax(pF) (a) (b) 图 3.1(a)设计约束的图形表示 (b) 频率范围加宽后的设计约束 根据第二章中的介绍,对于电感电容压控振荡器,其输出频率只和电感电容 值有关。由于在确定可变电容类型的情况下,可变电容的最大值和最小值的比值 是一定的。因此设计电感电容压控振荡器时需要考虑的独立变量最后可以归结到 功耗、电感几何参数(决定电感的感值大小 L0 和芯片面积)、可变电容最大值 Cmax(根据可变电容特性可确定其最小值 Cmin)和差分对管的宽度 W(决定等效负 阻大小。为了减小寄生电容和噪声,差分对管的长度 L 一般设为最小长度)这几个 参数。根据振荡器的性能指标,对于输出频率,其输出频率覆盖范围必须包含所 需频率范围,根据式(2.1)有: 2 max 0 min 1 > ω L C (3.1) 2 min 0 max 1 < ω L C (3.2) ωmax 与 ωmin 分别为频率范围要求的最高与最低频率。对于起振条件,振荡

第三章宽带压控振荡器的设计与优化 器的回路增益至少要大于起振因子α以保证电路可以正常起振[1],其数学形式可 表示为: gactive >agtank (3.3) 其中gactive为差分管跨导(有效负导纳),gtank为回路损耗导纳,即电感电容谐 振回路等效并联电阻的倒数。一般α不小于3才能保证电路正常起振。 对于振荡幅度,振荡器的输出振幅至少要大于振荡最小值Vmin: (3.4) gtank 因此,只要选定电感参数,在功耗一定的情况下,振荡器的设计要求就可以 在可变电容-差分对管宽度(Cmax-W)关系图上表示出来,如图3.1(a)。频率变化范 围(式(3.1),(3.2)在图中分别表示为tr1,tr2两条线,而在两条线之间的区域, 电容的取值能够满足频率覆盖范围要求。(3.3)式决定启动条件,在图中表现为 Start-up线,在其右边,即差分管宽度满足启动条件时,电路才能正常起振。Tank amplitude线表示振荡幅度要求,当电容值小于这条线时,振荡幅度满足要求。 因此,阴影区域表示满足所有约束条件下的Cmx和W参数值。一般优化步骤为 先选定Q值最大的电感参数,再确定电容值和差分对管宽度。 对于需要覆盖宽频率范围的压控振荡器而言,如果选定电感值不变,由于频 率变化范围增大,频率的上下限会分别上升下降,反应到Cmax-W图上则表示为 tr1线向下移动,而tr2线向上移动。这样当选择Q值最大的电感时,阴影区域有 可能不存在,即不存在满足所有指标的振荡器(图3.1(b)。减小电感值可以使t1 上移,tr2线下移,恢复到图3.1()时的状态。但需要注意的是,减小电感值的同 时,Start-up线会向右边移动,Tank amplitude线则会向下移,使得约束条件更 加苛刻。这样,设计者有可能不得不通过增大功耗来保证起振条件和振荡幅度要 求。因此,随着频率覆盖范围越来越宽,功耗,电感电容值等参数之间的权衡变 得更加重要。 3.2功耗的优化 根据第二章中的介绍,当压控振荡器工作在电流受限区域时,有: 2Ea=√2 En (3.5) 一般来说,压控振荡器会尽量避免工作在电压受限区域,因为在电压受限区 域时,能量有极大的浪费,反而会恶化相位噪声性能。理想状态是压控振荡器工 作在电流受限区和电压受限区的拐点处,此时振荡幅度正好达到最大值。从(3.5) 1g
第三章 宽带压控振荡器的设计与优化 14 器的回路增益至少要大于起振因子 α 以保证电路可以正常起振[1],其数学形式可 表示为: g > active tank αg (3.3) 其中 gactive为差分管跨导(有效负导纳),gtank 为回路损耗导纳,即电感电容谐 振回路等效并联电阻的倒数。一般 α 不小于 3 才能保证电路正常起振。 对于振荡幅度,振荡器的输出振幅至少要大于振荡最小值 Vmin: bias tank min tank I V = >V g (3.4) 因此,只要选定电感参数,在功耗一定的情况下,振荡器的设计要求就可以 在可变电容-差分对管宽度(Cmax-W)关系图上表示出来,如图 3.1(a)。频率变化范 围(式(3.1),(3.2))在图中分别表示为 tr1,tr2 两条线,而在两条线之间的区域, 电容的取值能够满足频率覆盖范围要求。(3.3)式决定启动条件,在图中表现为 Start-up 线,在其右边,即差分管宽度满足启动条件时,电路才能正常起振。Tank amplitude 线表示振荡幅度要求,当电容值小于这条线时,振荡幅度满足要求。 因此,阴影区域表示满足所有约束条件下的 Cmax和 W 参数值。一般优化步骤为 先选定 Q 值最大的电感参数,再确定电容值和差分对管宽度。 对于需要覆盖宽频率范围的压控振荡器而言,如果选定电感值不变,由于频 率变化范围增大,频率的上下限会分别上升下降,反应到 Cmax-W 图上则表示为 tr1 线向下移动,而 tr2 线向上移动。这样当选择 Q 值最大的电感时,阴影区域有 可能不存在,即不存在满足所有指标的振荡器(图 3.1(b))。减小电感值可以使 tr1 上移,tr2 线下移,恢复到图 3.1(a)时的状态。但需要注意的是,减小电感值的同 时,Start-up 线会向右边移动,Tank amplitude 线则会向下移,使得约束条件更 加苛刻。这样,设计者有可能不得不通过增大功耗来保证起振条件和振荡幅度要 求。因此,随着频率覆盖范围越来越宽,功耗,电感电容值等参数之间的权衡变 得更加重要。 3.2 功耗的优化 根据第二章中的介绍,当压控振荡器工作在电流受限区域时,有: tank tank tank tank 0 2E V = = 2E L ω C (3.5) 一般来说,压控振荡器会尽量避免工作在电压受限区域,因为在电压受限区 域时,能量有极大的浪费,反而会恶化相位噪声性能。理想状态是压控振荡器工 作在电流受限区和电压受限区的拐点处,此时振荡幅度正好达到最大值。从(3.5)

第三章宽带压控振荡器的设计与优化 式可看出,在电流受限区域振荡幅度是与振荡频率成正比的2]。对于宽带振荡器 来说,振荡频率ω,变化范围很大。假设振荡器最高频率为最低频率的两倍,则在 功耗不变的情况下,振荡频率最低时的振荡幅度只有最高频率时的二分之一,输 出振荡幅度的变化会带来以下问题: 一、在低输出频率时,振荡幅度有可能达不到要求或者干脆不能起振。 二、输出波形的振荡幅度变化幅度很大,对振荡器的后续电路性能产生影响。 例如:分频器的噪声和功耗就受制于振荡器的输出信号幅度:混频器的转换 增益也受信号幅度影响。 三、可变电容的等效电容值会随幅度变化而变化。 图3.2反型MOS管可变电容(IMOS) Cmax Cmin Vetr-V。 图3.3MOS可变电容 图3.4不同振荡幅度下的输出波形 以反型NMOS管(Inversion MOS)可变电容为例,在压控振荡器设计中,用 调谐电压Vctm控制NMOS管的源漏两端,栅极接至振荡器输出端Vo,这样NMOS 15
第三章 宽带压控振荡器的设计与优化 15 式可看出,在电流受限区域振荡幅度是与振荡频率成正比的[2]。对于宽带振荡器 来说,振荡频率ω0 变化范围很大。假设振荡器最高频率为最低频率的两倍,则在 功耗不变的情况下,振荡频率最低时的振荡幅度只有最高频率时的二分之一,输 出振荡幅度的变化会带来以下问题: 一、在低输出频率时,振荡幅度有可能达不到要求或者干脆不能起振。 二、输出波形的振荡幅度变化幅度很大,对振荡器的后续电路性能产生影响。 例如:分频器的噪声和功耗就受制于振荡器的输出信号幅度;混频器的转换 增益也受信号幅度影响。 三、可变电容的等效电容值会随幅度变化而变化。 图 3.2 反型 MOS 管可变电容(IMOS) 图 3.3 IMOS 可变电容 图 3.4 不同振荡幅度下的输出波形 以反型 NMOS 管(Inversion MOS)可变电容为例,在压控振荡器设计中,用 调谐电压 Vctrl 控制 NMOS 管的源漏两端,栅极接至振荡器输出端 Vo,这样 NMOS