第二章电感电容压控振荡器 第二章电感电容压控振荡器 随着片上电感仿真技术的成熟和理论分析的完善,电感电容压控振荡器在高 频应用方面己经成为主流振荡器结构。本章主要介绍了电容电感压控振荡器的基 本结构和主要性能指标。 2.1基本结构 Mp1 P1 P2 2Cv 0000 Mn Mn2 图21电感电容压控振荡器原理图 图2.1是差分互补M○S管电感电容压控振荡器的原理图[1]。实际电路设计 中,电感和电容总是会具有能量损耗,因此采用Mp1,Mp2与Mn1,Mn2组成 两对差分对管补偿振荡过程中的能量损耗,保证振荡器能够持续工作。电路总直 流电流即为电流源丨的大小。振荡器的输出频率由电感电容决定,如果考虑到器 件和版图的寄生电容,可以得到输出频率为: (2.1) LCtotal 其中Ctota=Cxed+Cv+Cpar,为输出节点P1,P2间总的等效电容。Cv为串联 压控可变电容大小,Cpar为P1,P2间总的寄生电容,Cxed为固定电容大小。压 控可变电容的值由电容两边的电压差值决定,因此,改变调谐电压Vc可以很方 便的改变输出频率。实际上,可以把压控振荡器看作一个将电压信号转化为具有 特定频率信号的振荡电路,其频率受到输入电压VM控制。 6
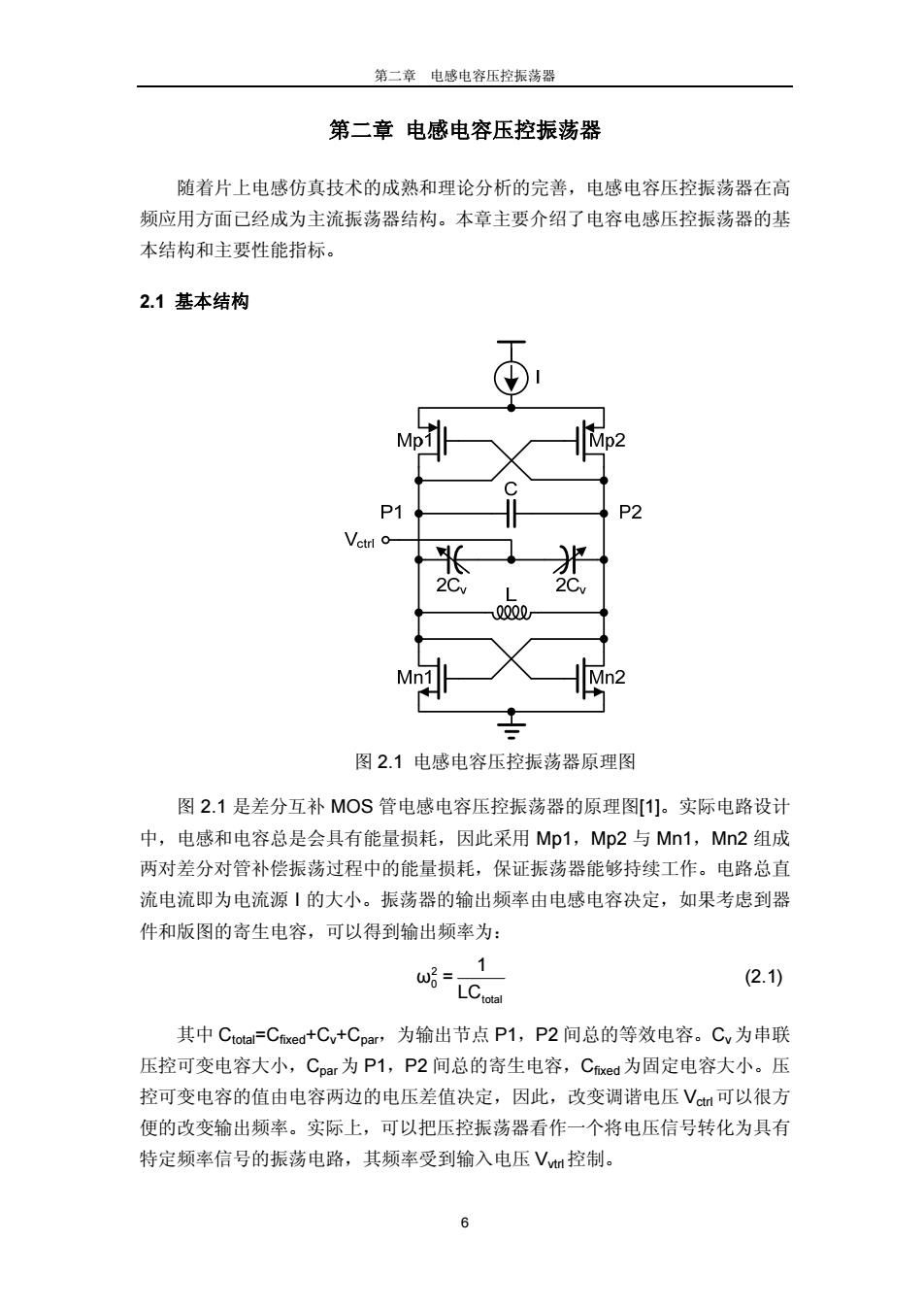
第二章 电感电容压控振荡器 6 第二章 电感电容压控振荡器 随着片上电感仿真技术的成熟和理论分析的完善,电感电容压控振荡器在高 频应用方面已经成为主流振荡器结构。本章主要介绍了电容电感压控振荡器的基 本结构和主要性能指标。 2.1 基本结构 图 2.1 电感电容压控振荡器原理图 图 2.1 是差分互补 MOS 管电感电容压控振荡器的原理图[1]。实际电路设计 中,电感和电容总是会具有能量损耗,因此采用 Mp1,Mp2 与 Mn1,Mn2 组成 两对差分对管补偿振荡过程中的能量损耗,保证振荡器能够持续工作。电路总直 流电流即为电流源 I 的大小。振荡器的输出频率由电感电容决定,如果考虑到器 件和版图的寄生电容,可以得到输出频率为: 2 0 total 1 ω = LC (2.1) 其中 Ctotal=Cfixed+Cv+Cpar,为输出节点 P1,P2 间总的等效电容。Cv 为串联 压控可变电容大小,Cpar为 P1,P2 间总的寄生电容,Cfixed为固定电容大小。压 控可变电容的值由电容两边的电压差值决定,因此,改变调谐电压 Vctrl 可以很方 便的改变输出频率。实际上,可以把压控振荡器看作一个将电压信号转化为具有 特定频率信号的振荡电路,其频率受到输入电压 Vvtrl 控制

第二章电感电容压控振荡器 2.2性能参数 2.2.1频率覆盖范围 根据式(2.1),可以知道振荡器的输出频率由等效电感和等效电容值决定。如 果可变电容Cv的变化范围从Cmin到Cmax, 则振荡器输出最小频率和最大频率分 别是: 1 o.min= (2.2) 2T/L(C ed +Cpar +Cmax) (2.3) 2TTL(Cwed+Cpar +Cmin) 对于可变电容来说,其能达到的最大电容值与最小电容值的比值不会超过一 个极限值a: Cmax<a (2.4) foma=2TL(C+Cpa+CmaC+Cpr+Cmax) C< (2.5) fomn2T√L(C+Car+Cmn)√c+Cpar+Cmn)VC min 可以看出,如果仅仅使用单一类型的可变电容,压控振荡器的最高与最低频 率比值会有一个极限。以SMIC0.18μn CMOS工艺库为例,其AMOS可变电容 最大与最小电容比值约为4,则用此类型可变电容设计的电感电容压控振荡器最 高与最低频率的比值不会超过2。因此,很难用此类型可变电容设计频率覆盖范 围超过50%的振荡器。 2.2.2振荡幅度 不同于理想电路特性,实际片上电感电容都存在串联电阻,图2.1中电感电 容压控振荡器的等效电路可以化为图2.2()所示,C,L分别为接在输出节点P1, P2上的总等效电容和电感。等效电感串联电阻和电容串联电阻的能量损耗由差 分对管等效成的负阻-R来补偿。其中R和Rc分别为电感和电容的串联电阻,由 于片上电容的品质因数通常要远大于片上电感,电感电容谐振回路的能量损耗主 要由片上电感的串联电阻引起。根据电感和电容的串联-并联转换关系,图2.2() 可以转换成图2.2(b)的等效电路。 根据能量守恒和转换的理论,在谐振回路中,存储在电感中的最大能量应该 >
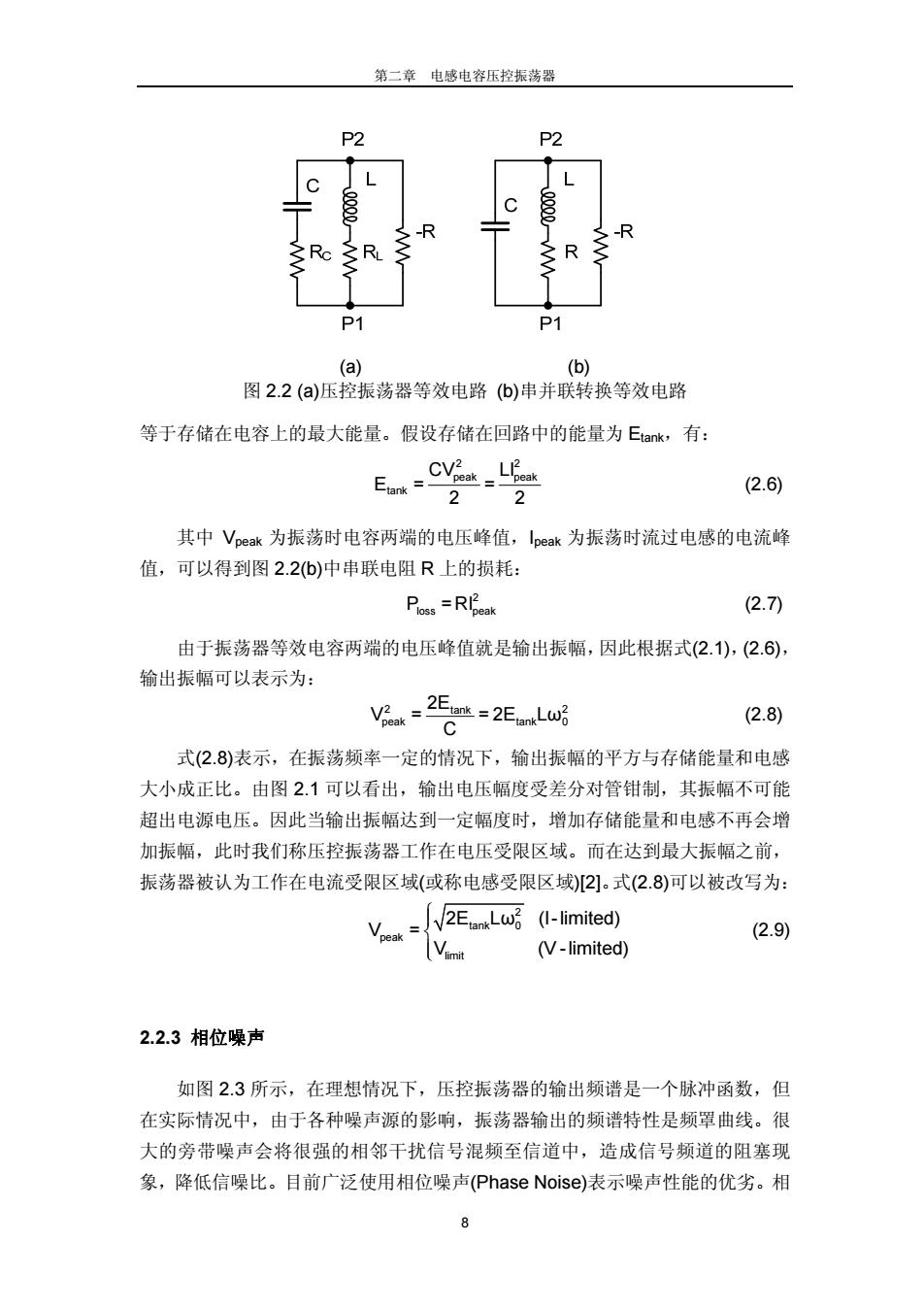
第二章 电感电容压控振荡器 7 2.2 性能参数 2.2.1 频率覆盖范围 根据式(2.1),可以知道振荡器的输出频率由等效电感和等效电容值决定。如 果可变电容 Cv 的变化范围从 Cmin到 Cmax,则振荡器输出最小频率和最大频率分 别是: 0,min fixed par max 1 f = 2π L(C +C +C ) (2.2) 0,max fixed par min 1 f = 2π L(C +C +C ) (2.3) 对于可变电容来说,其能达到的最大电容值与最小电容值的比值不会超过一 个极限值 α: max min C < α C (2.4) 0,max par max par max max 0,min par min par min min f 2π L(C+C +C ) (C+C +C ) C = = << α f C 2π L(C+C +C ) (C+C +C ) (2.5) 可以看出,如果仅仅使用单一类型的可变电容,压控振荡器的最高与最低频 率比值会有一个极限。以 SMIC 0.18μm CMOS 工艺库为例,其 AMOS 可变电容 最大与最小电容比值约为 4,则用此类型可变电容设计的电感电容压控振荡器最 高与最低频率的比值不会超过 2。因此,很难用此类型可变电容设计频率覆盖范 围超过 50%的振荡器。 2.2.2 振荡幅度 不同于理想电路特性,实际片上电感电容都存在串联电阻,图 2.1 中电感电 容压控振荡器的等效电路可以化为图 2.2(a)所示,C,L 分别为接在输出节点 P1, P2 上的总等效电容和电感。等效电感串联电阻和电容串联电阻的能量损耗由差 分对管等效成的负阻-R 来补偿。其中 RL和 RC分别为电感和电容的串联电阻,由 于片上电容的品质因数通常要远大于片上电感,电感电容谐振回路的能量损耗主 要由片上电感的串联电阻引起。根据电感和电容的串联-并联转换关系,图 2.2(a) 可以转换成图 2.2(b)的等效电路。 根据能量守恒和转换的理论,在谐振回路中,存储在电感中的最大能量应该
第二章电感电容压控振荡器 P2 P2 L -R 及R P1 P1 (a) (b) 图2.2()压控振荡器等效电路(b)串并联转换等效电路 等于存储在电容上的最大能量。假设存储在回路中的能量为Eak,有: Etank CV peak 22 (2.6) 其中Vpeak为振荡时电容两端的电压峰值,Ipeak为振荡时流过电感的电流峰 值,可以得到图2.2(b)中串联电阻R上的损耗: Pioss =Rlpeak (2.7) 由于振荡器等效电容两端的电压峰值就是输出振幅,因此根据式(2.1),(2.6), 输出振幅可以表示为: V-2Es-2ELw (2.8) C 式(28)表示,在振荡频率一定的情况下,输出振幅的平方与存储能量和电感 大小成正比。由图2.1可以看出,输出电压幅度受差分对管钳制,其振幅不可能 超出电源电压。因此当输出振幅达到一定幅度时,增加存储能量和电感不再会增 加振幅,此时我们称压控振荡器工作在电压受限区域。而在达到最大振幅之前, 振荡器被认为工作在电流受限区域(或称电感受限区域)[2]。式(2.8)可以被改写为: √2 EankLw--limited)) (2.9) (V-limited) 2.2.3相位噪声 如图2.3所示,在理想情况下,压控振荡器的输出频谱是一个脉冲函数,但 在实际情况中,由于各种噪声源的影响,振荡器输出的频谱特性是频罩曲线。很 大的旁带噪声会将很强的相邻干扰信号混频至信道中,造成信号频道的阻塞现 象,降低信噪比。目前广泛使用相位噪声(Phase Noise)表示噪声性能的优劣。相 8
第二章 电感电容压控振荡器 8 (a) (b) 图 2.2 (a)压控振荡器等效电路 (b)串并联转换等效电路 等于存储在电容上的最大能量。假设存储在回路中的能量为 Etank,有: 2 2 peak peak tank CV LI E= = 2 2 (2.6) 其中 Vpeak 为振荡时电容两端的电压峰值,Ipeak 为振荡时流过电感的电流峰 值,可以得到图 2.2(b)中串联电阻 R 上的损耗: 2 P =RI loss peak (2.7) 由于振荡器等效电容两端的电压峰值就是输出振幅,因此根据式(2.1),(2.6), 输出振幅可以表示为: 2 2 tank peak tank 0 2E V = = 2E Lω C (2.8) 式(2.8)表示,在振荡频率一定的情况下,输出振幅的平方与存储能量和电感 大小成正比。由图 2.1 可以看出,输出电压幅度受差分对管钳制,其振幅不可能 超出电源电压。因此当输出振幅达到一定幅度时,增加存储能量和电感不再会增 加振幅,此时我们称压控振荡器工作在电压受限区域。而在达到最大振幅之前, 振荡器被认为工作在电流受限区域(或称电感受限区域)[2]。式(2.8)可以被改写为: ⎧⎪ ⎨ ⎪⎩ 2 tank 0 peak limit 2E Lω (I-limited) V = V (V -limited) (2.9) 2.2.3 相位噪声 如图 2.3 所示,在理想情况下,压控振荡器的输出频谱是一个脉冲函数,但 在实际情况中,由于各种噪声源的影响,振荡器输出的频谱特性是频罩曲线。很 大的旁带噪声会将很强的相邻干扰信号混频至信道中,造成信号频道的阻塞现 象,降低信噪比。目前广泛使用相位噪声(Phase Noise)表示噪声性能的优劣。相
第二章电感电容压控振荡器 位噪声的定义为Hz内单边带噪声谱密度与载波功率比值的分贝形式: L{△w}=10Ilog Psideband(w,+△w,1Hz) (2.10) 其中△ω为频率偏移量,ω。为载波频率。相位噪声是衡量压控振荡器乃至频 率综合器性能最主要的指标之一,在系统中,压控振荡器的相位噪声是直接影响 到灵敏度的最主要因素。 Ideal Oscillator Actual Oscillator 00 图2.3压控振荡器的频谱 L{△w汁 f3 1 Wo AW1 ω 图2.4典型相位噪声曲线 一个典型的压控振荡器的相位噪声曲线如图2.4,大致可分为三个区域,在 近频端相位噪声斜率为-30dB/10倍频,称为1区域,在稍远端相位噪声斜率为 -20B/10倍频偏,称为1?区域;最远端是振荡器本身的白噪声区域3]。1R区 域与1P区域之间分界点称为拐点频率△ω。具有1P特性的相位噪声由振荡 器器件的闪烁噪声所引起,而具有1?特性的相位噪声则是由器件的白噪声所引 起。压控振荡器的器件噪声主要来源于谐振电感和电容的串联寄生电阻,差分对
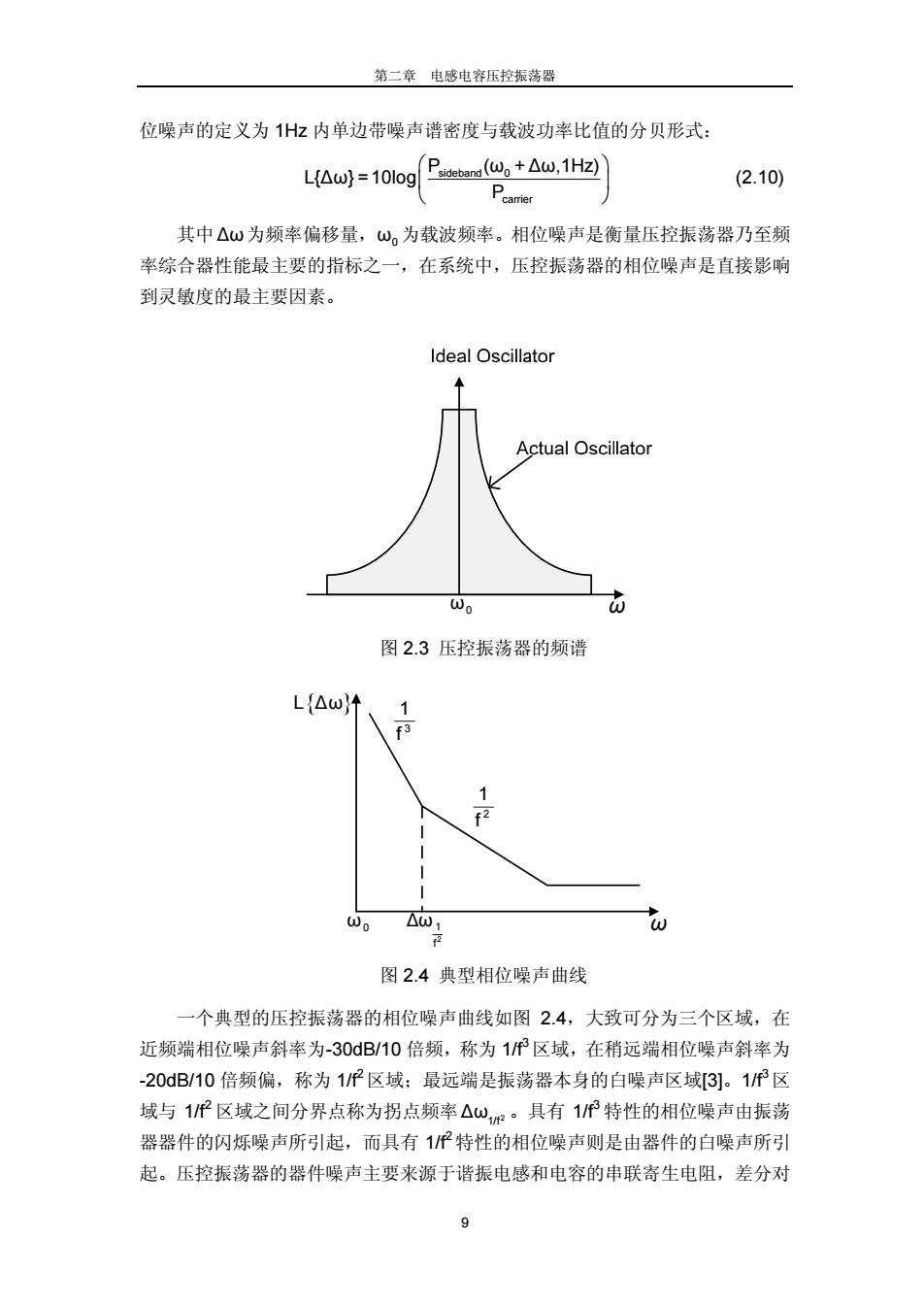
第二章 电感电容压控振荡器 9 位噪声的定义为 1Hz 内单边带噪声谱密度与载波功率比值的分贝形式: ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ sideband 0 carrier P (ω +Δω,1Hz) L{Δω} =10log P (2.10) 其中Δω为频率偏移量,ω0 为载波频率。相位噪声是衡量压控振荡器乃至频 率综合器性能最主要的指标之一,在系统中,压控振荡器的相位噪声是直接影响 到灵敏度的最主要因素。 ω0 ω 图 2.3 压控振荡器的频谱 ω0 ω L{Δω} 3 1 f 2 1 f 2 1 f Δω 图 2.4 典型相位噪声曲线 一个典型的压控振荡器的相位噪声曲线如图 2.4,大致可分为三个区域,在 近频端相位噪声斜率为-30dB/10 倍频,称为 1/f3区域,在稍远端相位噪声斜率为 -20dB/10 倍频偏,称为 1/f2区域;最远端是振荡器本身的白噪声区域[3]。1/f3区 域与 1/f2 区域之间分界点称为拐点频率 2 1/f Δω 。具有 1/f3 特性的相位噪声由振荡 器器件的闪烁噪声所引起,而具有 1/f2特性的相位噪声则是由器件的白噪声所引 起。压控振荡器的器件噪声主要来源于谐振电感和电容的串联寄生电阻,差分对

第二章电感电容压控振荡器 管和尾电流源。 目前,相位噪声的分析方法和理论主要可以分为三大类:线性时不变(L1, Linear Time Invariant)分析[4,5],非线性时不变(NTl,Nonlinear Time Invariant) 分析[6]和线性相位时变(LPTV,Linear Phase Time Varying)分析[7,8]。其中由 Hajimiri提出的线性相位时变噪声模型可以分析单个噪声源对相位噪声的贡献, 精确计算相位噪声,系统的阐述了产生相位噪声的各个区域的噪声来源,因此得 到了广泛采用。 三种相位噪声的模型分析显示,在1区域的相位噪声可以表示为: LA) KT W (2.11) 2Pig Q2Aw2 其中Q为谐振回路总的品质因数,振荡信号能量Pg∝V*。可以得出,增 大振荡信号幅度和提高谐振回路的品质因数可以优化相位噪声性能。由于片上可 变电容的品质因数要远远大于片上电感,总谐振回路的品质因数完全取决于电 感。因此,设计一个品质因数高、感值合理的电感往往是振荡器设计和优化的第 一步。 2.2.4调谐增益 调谐增益是压控振荡器的一个重要参数,其定义为: Kvco= Afout Vett (2.12) 其中fout为压控振荡器的输出频率,Vctm为振荡器的调谐电压。 调谐增益直接反映了该压控振荡器输出频率对压控电压的敏感程度,在锁相 环的传递函数中起着重要作用。图2.5是一个典型的三阶频率综合器的$域模型 [9,1O],其中lcp为电荷泵(CP)的电流,Z(s)为环路滤波器(Loop Filter)的传递函 数,Kvco为压控振荡器(VCO)的增益,N为分频器(Divider)的分频比,可以得到 频率综合器的开环传递函数为: Ho)= Kyco (2.13) 2m×N 环路滤波器为二阶无源电阻电容网络(图2.6),其传递函数可以写为: Zr)=1 s+w (2.14) C2 S(s+Wp2) 其中: 10
第二章 电感电容压控振荡器 10 管和尾电流源。 目前,相位噪声的分析方法和理论主要可以分为三大类:线性时不变(LTI, Linear Time Invariant)分析[4, 5],非线性时不变(NTI, Nonlinear Time Invariant) 分析[6]和线性相位时变(LPTV, Linear Phase Time Varying)分析[7, 8]。其中由 Hajimiri 提出的线性相位时变噪声模型可以分析单个噪声源对相位噪声的贡献, 精确计算相位噪声,系统的阐述了产生相位噪声的各个区域的噪声来源,因此得 到了广泛采用。 三种相位噪声的模型分析显示,在 1/f2区域的相位噪声可以表示为: ∝ 2 0 2 2 sig KT ω L{Δω} 2P Q Δω (2.11) 其中 Q 为谐振回路总的品质因数,振荡信号能量 ∝ 2 P V sig peak 。可以得出,增 大振荡信号幅度和提高谐振回路的品质因数可以优化相位噪声性能。由于片上可 变电容的品质因数要远远大于片上电感,总谐振回路的品质因数完全取决于电 感。因此,设计一个品质因数高、感值合理的电感往往是振荡器设计和优化的第 一步。 2.2.4 调谐增益 调谐增益是压控振荡器的一个重要参数,其定义为: out VCO ctrl Δf K = ΔV (2.12) 其中 fout为压控振荡器的输出频率,Vctrl 为振荡器的调谐电压。 调谐增益直接反映了该压控振荡器输出频率对压控电压的敏感程度,在锁相 环的传递函数中起着重要作用。图 2.5 是一个典型的三阶频率综合器的 s 域模型 [9, 10],其中 Icp为电荷泵(CP)的电流,ZF(s)为环路滤波器(Loop Filter)的传递函 数,KVCO 为压控振荡器(VCO)的增益,N 为分频器(Divider)的分频比,可以得到 频率综合器的开环传递函数为: × × cp VCO o(s) F(s) I K H= Z 2π×N s (2.13) 环路滤波器为二阶无源电阻电容网络(图 2.6),其传递函数可以写为: z F(s) 2 p2 1 s+ω Z = C s(s+ω ) (2.14) 其中: