CMOS运放的设计和几何规划优化方法研究

CMOS运放的设计和几何规划优化方法研究 目录 摘要… 第一章 绪论·…。 第二章两级运算放大器 S21电路及设计指标…3 $22性能参数与约束条件的简略分析…4 第三章手工设计及仿真结果 §3.1手工计算…。10 §3.2结合HSPICE模拟调整参数值····13 §3.3运放的仿真测试结果·14 第四章几何规划(GP)优化方法设计运放 S4.1 GPCAD简介. §4.2几何规划优化设计…。 …19 §4.3Mosk标准格式的公式整理·22 §4.4优化结果…29 §4.5设计不足与讨论…31 附录…32 参考文献…35 致谢… …35

CMOS 运放的设计和几何规划优化方法研究 目录 摘要··········································2 第一章 绪论··································2 第二章 两级运算放大器 §2.1 电路及设计指标······················3 §2.2 性能参数与约束条件的简略分析·········4 第三章 手工设计及仿真结果 §3.1 手工计算···························10 §3.2 结合 HSPICE 模拟调整参数值··········13 §3.3 运放的仿真测试结果··················14 第四章 几何规划(GP)优化方法设计运放 §4.1 GPCAD 简介·························18 §4.2 几何规划优化设计····················19 §4.3 Mosek 标准格式的公式整理·············22 §4.4 优化结果····························29 §4.5 设计不足与讨论······················31 附录··········································32 参考文献······································35 致谢··········································35 1

CMOS运放的设计和几何规划优化方法研究 摘要 随着SOC、混合信号集成电路的发展，作为数字芯片与外部世界的接口电路一模拟 集成电路的设计变得越来越重要。但随着电路复杂性的不断提高以及设计周期的限制，一直 以来采用的以经验为主的设计方法已经越来越不能适应集成电路产业的高速发展，本文就介 绍了一种采用数学最优化方法一一Geometric Programming(几何规划)对两级运放的设计进 行优化的方法。通常情况下，我们采用手工计算与SPICE仿真相结合的方法来设计运放。 但在这个过程中，有些参数的选取完全就要靠设计者的经验，因而最终得到的结果往往只是 局部的最优解。而几何规划(GP)方法是根据设计要求，通过运放设计的一般步骤，得到 需要优化的目标函数以及它的一系列约束不等式、约束等式，然后将它们转化成一个几何规 划问题，最后采用数学优化求解方法求得一个全局最优解。 关键词： 模拟集成电路CAD、运算放大器、Geometric Programming、几何规划优化 第一章 绪论 随着集成电路的发展，电路设计己经与EDA工具密不可分。在数字集成电路的设计领 域，逻辑综合与自动布局布线的设计方法已经非常成熟；然而到目前为止，仍然没有一个成 熟的模拟电路CAD解决方案。在研究领域，许多学者提出了各种各样的优化算法，致力于 解决模拟电路的自动综合技术。Geometric Programming(几何规划)优化设计方法就是其中 的一种。该优化方法的基本思想是把模拟电路的性能指标转化成数学程序，从而运用数学方 法来解决其电路最优配置问题。由于运放在$OC、大规模混合集成电路等中的应用极其广 泛，在不同的使用场合需要不同的性能要求，若使用手工设计与SPICE仿真相结合的方法， 就不得不对每一个具体的性能指标都从头开始设计，不仅费时、费力，还不一定能够得到最 优的设计结果；而采用几何规划优化的设计方法，则只需将变动的性能指标带入程序，就可 以方便、快速地得到最优的设计方案，从而实现了“复用”设计。 本文结构方面是如下安排的。第二章给出一种ULSI中常用的两级运放的电路及要求达 到的性能指标，并对其设计原理进行一些简单的分析与介绍。第三章运用手工计算与SPICE 仿真相结合的方法对该运放的参数进行设计并给出仿真结果。第四章运用GP优化的方法对 该运放参数进行设计，并将仿真结果与第三部分的仿真结果进行分析比较。最后在附录中列 出了设计与模拟过程中用到的模型。 2

CMOS 运放的设计和几何规划优化方法研究 摘要 随着 SOC、混合信号集成电路的发展，作为数字芯片与外部世界的接口电路——模拟 集成电路的设计变得越来越重要。但随着电路复杂性的不断提高以及设计周期的限制，一直 以来采用的以经验为主的设计方法已经越来越不能适应集成电路产业的高速发展，本文就介 绍了一种采用数学最优化方法——Geometric Programming(几何规划)对两级运放的设计进 行优化的方法。通常情况下，我们采用手工计算与 SPICE 仿真相结合的方法来设计运放。 但在这个过程中，有些参数的选取完全就要靠设计者的经验，因而最终得到的结果往往只是 局部的最优解。而几何规划（GP）方法是根据设计要求，通过运放设计的一般步骤，得到 需要优化的目标函数以及它的一系列约束不等式、约束等式，然后将它们转化成一个几何规 划问题，最后采用数学优化求解方法求得一个全局最优解。 关键词： 模拟集成电路 CAD、运算放大器、Geometric Programming、几何规划优化 第一章 绪论 随着集成电路的发展，电路设计已经与 EDA 工具密不可分。在数字集成电路的设计领 域，逻辑综合与自动布局布线的设计方法已经非常成熟；然而到目前为止，仍然没有一个成 熟的模拟电路 CAD 解决方案。在研究领域，许多学者提出了各种各样的优化算法，致力于 解决模拟电路的自动综合技术。Geometric Programming（几何规划）优化设计方法就是其中 的一种。该优化方法的基本思想是把模拟电路的性能指标转化成数学程序，从而运用数学方 法来解决其电路最优配置问题。由于运放在 SOC、大规模混合集成电路等中的应用极其广 泛，在不同的使用场合需要不同的性能要求，若使用手工设计与 SPICE 仿真相结合的方法， 就不得不对每一个具体的性能指标都从头开始设计，不仅费时、费力，还不一定能够得到最 优的设计结果；而采用几何规划优化的设计方法，则只需将变动的性能指标带入程序，就可 以方便、快速地得到最优的设计方案，从而实现了“复用”设计。 本文结构方面是如下安排的。第二章给出一种 ULSI 中常用的两级运放的电路及要求达 到的性能指标，并对其设计原理进行一些简单的分析与介绍。第三章运用手工计算与 SPICE 仿真相结合的方法对该运放的参数进行设计并给出仿真结果。第四章运用 GP 优化的方法对 该运放参数进行设计，并将仿真结果与第三部分的仿真结果进行分析比较。最后在附录中列 出了设计与模拟过程中用到的模型。 2

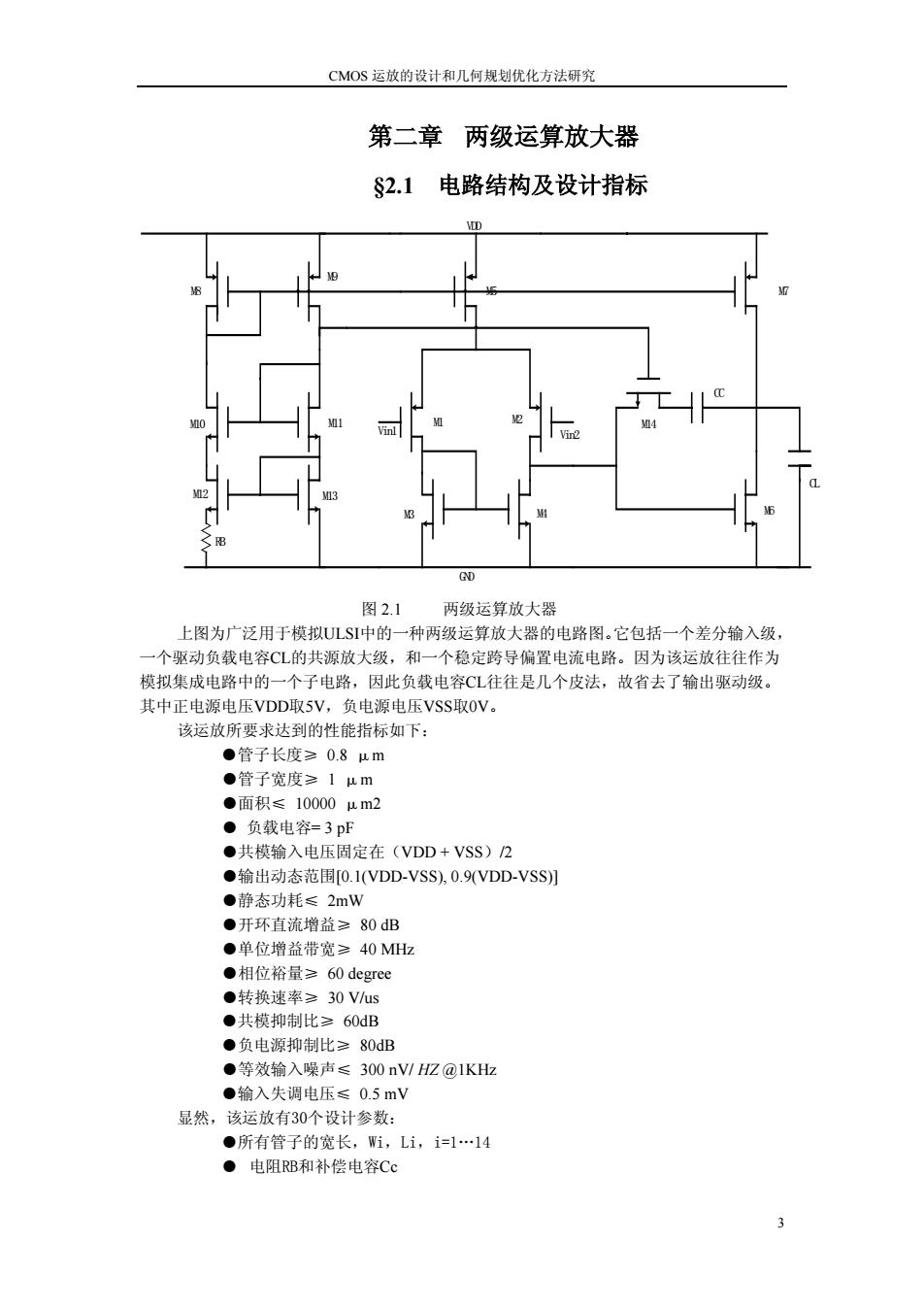
CMOS运放的设计和几何规划优化方法研究 第二章两级运算放大器 S2.1电路结构及设计指标 D QD 图2.1 两级运算放大器 上图为广泛用于模拟ULSI中的一种两级运算放大器的电路图。它包括一个差分输入级， 一个驱动负载电容CL的共源放大级，和一个稳定跨导偏置电流电路。因为该运放往往作为 模拟集成电路中的一个子电路，因此负载电容CL往往是几个皮法，故省去了输出驱动级。 其中正电源电压VDD取5V,负电源电压VSS取OV。 该运放所要求达到的性能指标如下： ●管子长度≥0.8μm ●管子宽度≥1um ●面积≤100004m2 ●负载电容=3pF ●共模输入电压固定在(VDD+VSS)2 ●输出动态范围[0.1(VDD-VSS),0.9VDD-VSS)] ●静态功耗≤2mW ●开环直流增益≥80dB ●单位增益带宽≥40MHz ●相位裕量≥60 degree ●转换速率≥30Vus ●共模抑制比≥60dB ●负电源抑制比≥80dB ●等效输入噪声≤300nV/HZ@1KHz ●输入失调电压≤0.5mV 显然，该运放有30个设计参数： ●所有管子的宽长，Wi,Li,i=1…14 ●电阻RB和补偿电容Cc 3

CMOS 运放的设计和几何规划优化方法研究 第二章 两级运算放大器 §2.1 电路结构及设计指标 VDD Vin2 M2 M3 M4 Vin1 M1 M5 GND M7 CC M14 CL M6 M8 M9 M10 M11 M12 M13 RB 图 2.1 两级运算放大器 上图为广泛用于模拟ULSI中的一种两级运算放大器的电路图。它包括一个差分输入级， 一个驱动负载电容CL的共源放大级，和一个稳定跨导偏置电流电路。因为该运放往往作为 模拟集成电路中的一个子电路，因此负载电容CL往往是几个皮法，故省去了输出驱动级。 其中正电源电压VDD取5V，负电源电压VSS取0V。 该运放所要求达到的性能指标如下： ●管子长度≥ 0.8 μm ●管子宽度≥ 1 μm ●面积≤ 10000 μm2 ● 负载电容= 3 pF ●共模输入电压固定在（VDD + VSS）/2 ●输出动态范围[0.1(VDD-VSS), 0.9(VDD-VSS)] ●静态功耗≤ 2mW ●开环直流增益≥ 80 dB ●单位增益带宽≥ 40 MHz ●相位裕量≥ 60 degree ●转换速率≥ 30 V/us ●共模抑制比≥ 60dB ●负电源抑制比≥ 80dB ●等效输入噪声≤ 300 nV/ HZ @1KHz ●输入失调电压≤ 0.5 mV 显然，该运放有30个设计参数： ●所有管子的宽长，Wi，Li，i=1…14 ● 电阻RB和补偿电容Cc 3

CMOS运放的设计和几何规划优化方法研究 $22性能参数与约束条件的简略分析 (1)开环增益AV 如图2.2为两级放大器的差分输入级 GND 图2.2运放的差分输入级 第一级增益An=-GnR=-g.(ralr),第二级为M6&M7组成的共源放大器，增益 Ar2=-GR2=-86（r6‖ro7) 所以整个放大器的增益为： Ar= 8 86 8a+8八86+8o7 2Cor WW. (aw+p.,L7, (2)频率特性与相位补偿 该电路共存在四个极点： (1)补偿电容引入的主极点： G g.2+84 @-A:+)Cc (A:+)Cc 其中CC=Cc+C6,因此由密勒效应形成的该极点是一个主极点。 (2) 输出极点 该极点由输出电容CL引起。忽略掉一些寄生电容，则 0一一8，该极点是第二极点。 C 4

CMOS 运放的设计和几何规划优化方法研究 §2.2 性能参数与约束条件的简略分析 （1）开环增益Av 如图2.2为两级放大器的差分输入级 V b i a s V D D V o u t V i n 2 M 2 M 3 M 4 V i n 1 M 1 M 5 G N D 图 2.2 运放的差分输入级 第一级增益 ( ) 1 1 1 2 V o 1 A R Gm g m r o = − = − & r o4 ，第二级为M6&M7组成的共源放大器，增益 ( ) 2 2 2 6 V o 6 A R Gm g m r o = − = − & r o7 。 所以整个放大器的增益为： 2 6 2 4 6 7 m m V o o o o g g A g g g g ⎛ ⎞⎛ = ⎜ ⎟⎜ ⎜ ⎟ + + ⎜ ⎝ ⎠⎝ ⎞ ⎟ ⎟ ⎠ = ( ) 2 6 2 2 617 2 OX N P N P C W L L I I µ µ λ λ+ W （2）频率特性与相位补偿 该电路共存在四个极点： （1） 补偿电容引入的主极点： ( ) ' ' ( ) 1 2 1 2 2 1 1 o o p C C G g go4 A A C C ω + = = + + 其中 ' C gd 6，因此由密勒效应形成的该极点是一个主极点。 C C C = +C （2） 输出极点 该极点由输出电容CL引起。忽略掉一些寄生电容，则 m6 pout L g C ω ≈ ，该极点是第二极点。 4

CMOS运放的设计和几何规划优化方法研究 (3) 镜像极点 81 C+C+C+C+Co 2Cm 2 该极点是第三极点 (4) 寄生极点 该极点存在与Cc与M14消除正向零点的回路中。 RC 其中C,=C6+C则4+C2+C4+C 密勒电容Cc实现了对放大器的频率补偿，但同时由于有了通过Cc的正馈通路，因而产 生了一个位于右半平面的零点0.-8，该零点将引入负的相位平移，使得相位裕量减小， Ce 运放的稳定性变差。 为了消除该零点对相位的影响，可以引入一个工作在线形区的14管，作为一个电阻与 Cc共同构成反馈回路。串联上这个电阻之后，引入的零点将会移动，即). 1 Ceg-R-m) 可见，R:值的选取将会决定这个正馈零点被搬移到的位置。这时候一般可以采用对M14的 两种取值方法来解决这个问题。 第一种方法，即参考资料[2]、[3]中采用的方法是取R.=g,这样o.将被推到无穷 远处，自然就不会对相位产生什么影响。 第二种方法，也是我认为更好的一种方法。是利用这个零点可以被搬移的特点，将该 正馈零点从右半平面搬移到对相位没有影响的左半平面，且选取M14的适当值，使得该零点 刚好位于第一非主极点的位置。这样，不仅可以消除该零点对相位裕量的影响，还可以抵消 掉第一非主极点对相位的影响，从而减轻了相位裕量对设计指标的限制，进而可以增大单位 增益带宽，提高运放的性能。 那么M14的尺寸选取是如何确定的呢？ ·0: CelgRu) 而该运放的第一非主极点位于左半平面，且0， 一8s, 可以令 1 8 Ce(8--R) →Rm 、C+Cc Ccgn 5

CMOS 运放的设计和几何规划优化方法研究 （3） 镜像极点 3 3 3 413 1 3 2 2 m m T pmirror gs gs db db gd gs g g C C C C C C ω ω = ≈ + + + + ≈ 该极点是第三极点 （4） 寄生极点 该极点存在与Cc与M14消除正向零点的回路中。 4 14 1 1 p Ron C ω = 其中C C1 6 gs g C d 4 Cdb2 Cdb4 Cg 2 = + +++ d 密勒电容Cc实现了对放大器的频率补偿，但同时由于有了通过Cc的正馈通路，因而产 生了一个位于右半平面的零点 m6 z C g C ω = ，该零点将引入负的相位平移，使得相位裕量减小， 运放的稳定性变差。 为了消除该零点对相位的影响，可以引入一个工作在线形区的M14管，作为一个电阻与 Cc共同构成反馈回路。串联上这个电阻之后，引入的零点将会移动，即 1 14 6 1 z on CC g m R ω − ≈ ⎛ ⎞ ⎜ ⎟ − ⎝ ⎠ 可见， Ron14 值的选取将会决定这个正馈零点被搬移到的位置。这时候一般可以采用对M14的 两种取值方法来解决这个问题。 第一种方法，即参考资料[2]、[3]中采用的方法是取 Ron14 = 1 g m6 − ，这样ωz 将被推到无穷 远处，自然就不会对相位产生什么影响。 第二种方法，也是我认为更好的一种方法。是利用这个零点可以被搬移的特点，将该 正馈零点从右半平面搬移到对相位没有影响的左半平面，且选取M14的适当值，使得该零点 刚好位于第一非主极点的位置。这样，不仅可以消除该零点对相位裕量的影响，还可以抵消 掉第一非主极点对相位的影响，从而减轻了相位裕量对设计指标的限制，进而可以增大单位 增益带宽，提高运放的性能。 那么 M14 的尺寸选取是如何确定的呢？ ( ) 1 14 6 1 z CC g m Ron ω − ≈ − ∵ 而该运放的第一非主极点位于左半平面，且 m6 p L g C ω − ≈ ， ∴ 可以令 ( ) 6 1 14 6 1 m L C m on g C g R C − − = − 14 6 L C on C m C C R C g + ⇒ ≈ 5