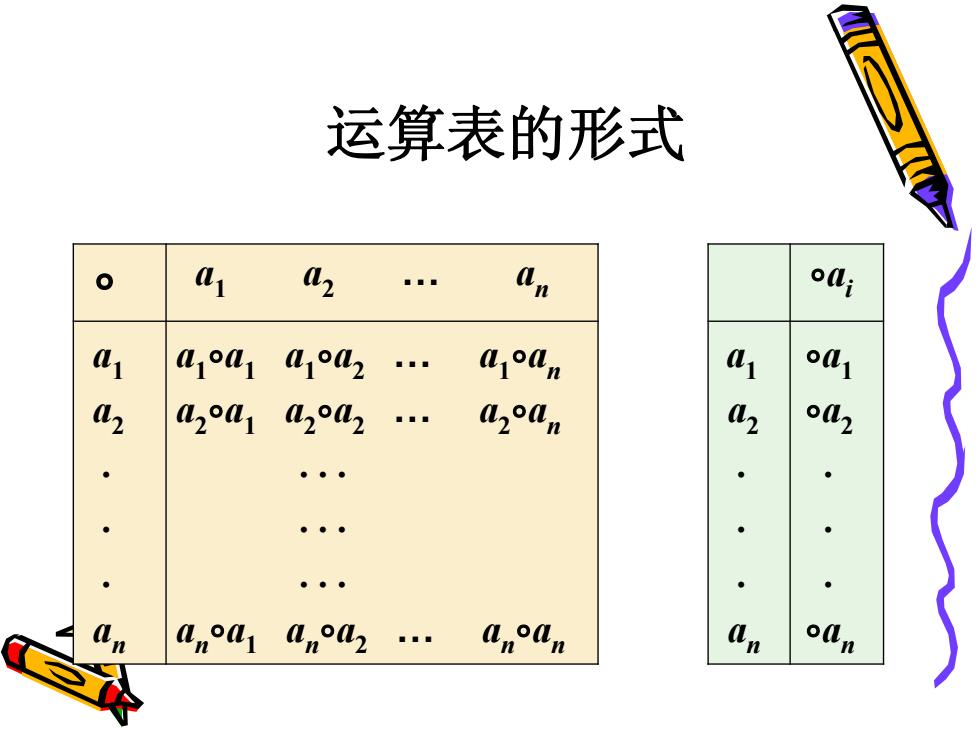
运算表的形式 01 4z oli a L11L12 . a san a o 2 doa aoa u2°n 。● Lm°01ano2 . anan
运算表的形式 ∘ a1 a2 . an ∘ai a1 a2 . . . an a1 ∘a1 a1 ∘a2 . a1 ∘an a2 ∘a1 a2 ∘a2 . a2 ∘an . . . . . . . . . an ∘a1 an ∘a2 . an ∘an a1 a2 . . . an ∘a1 ∘a2 . . . ∘an
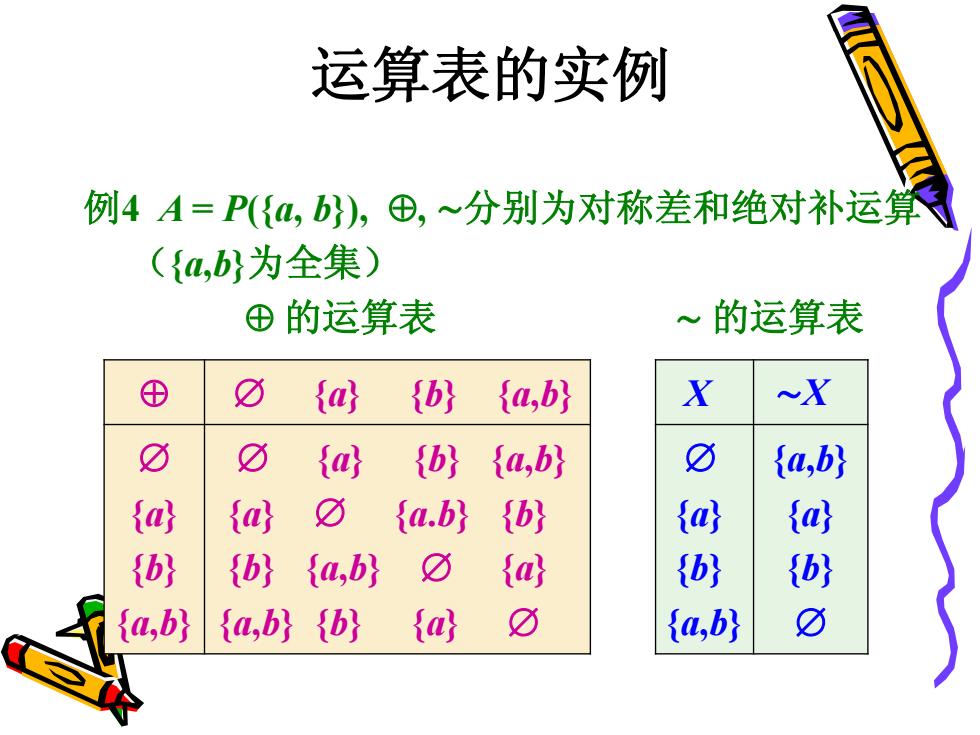
运算表的实例 例4A=P({,}),⊕,~分别为对称差和绝对补运算 ({,b}为全集) ⊕的运算表 的运算表 ⊕ ☑ a {b} {a,b} X ~X ☑ 0 a {b}{a,b} 0 {a,b} fa, { fa.by (by ta (a, (b {b} {a,b} 0 (a {b} {b) {a,b} {a,b}{b} \a 0 {a,b} 0
运算表的实例 例4 A = P({a, b}), , ∼分别为对称差和绝对补运算 ({a,b}为全集) 的运算表 ∼ 的运算表 {a} {b} {a,b} X ∼X {a} {b} {a,b} {a} {b} {a,b} {a} {a.b} {b} {b} {a,b} {a} {a,b} {b} {a} {a} {b} {a,b} {a,b} {a} {b}

·代数运算性质 定义 设*是集合S上的二元运算, 如果对于S中任意两个元素a,b,等式 a*b=b*a都成立, 则称运算*S上是可交换的,或者说* 满足交换律
• 代数运算性质 定义 设 * 是集合S上的二元运算, 如果对于S中任意两个元素a,b,等式 a * b = b * a 都成立, 则称运算* S上是可交换的,或者说* 满足交换律

定义设*是集合$上的二元运算, 如果对于S中任意三个元素a,b,c, 等式(a*b)*c=a*(b*c) 都成立,则称运算*在S上是可结合的 或者说*满足结合律
定义 设 * 是集合S上的二元运算, 如果对于S中任意三个元素a,b,c, 等式(a * b) * c = a * (b * c) 都成立,则称运算*在S上是可结合的, 或者说*满足结合律