第五章相似矩阵与二次型向量的长度及性质二、定义5.1.2向量的长度具有下述性质:1.非负性 当a1 0时,a>0;当a =0时,α=02. 齐次性 α l = [ Ilal;3.三角不等式 a +bla+b
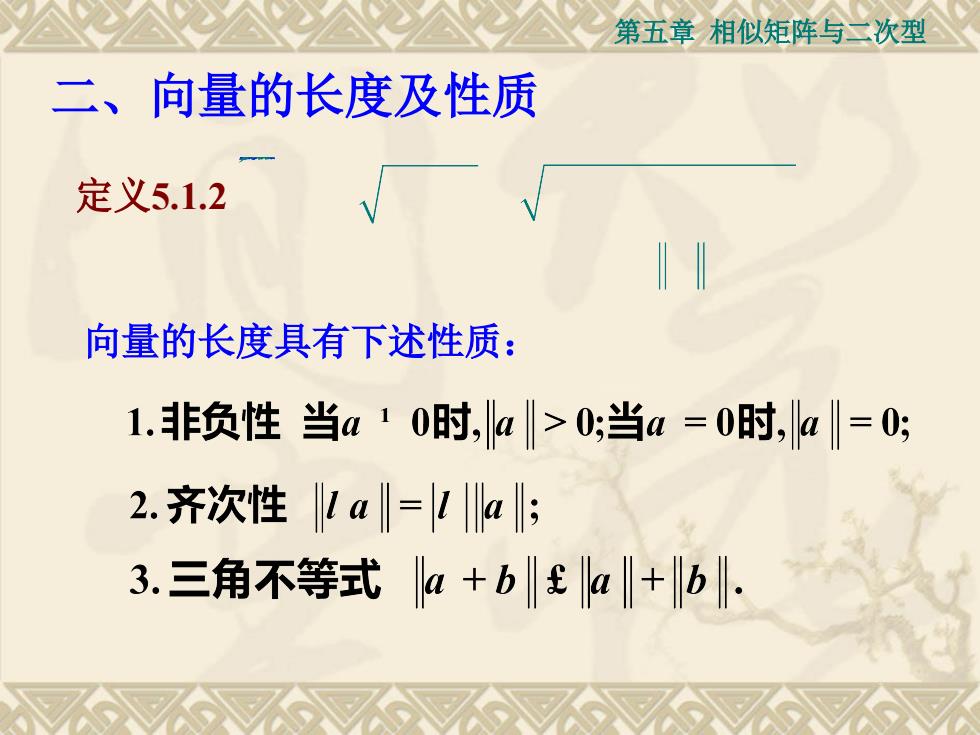
第五章 相似矩阵与二次型 定义5.1.2 向量的长度具有下述性质: 二、向量的长度及性质

第五章相似矩阵与二次型如果a就是一个与a同方向的单位向量a称为把向量α单位化,例2 α=(1,2,1),把α单位化得:121(1,2,1) =α]
第五章 相似矩阵与二次型

第五章相似矩阵与二次型例3 α = (1,2,1)T,β= (3,-1,4)55则e=arccosarccosV6V262V39
第五章 相似矩阵与二次型

第五章相似矩阵与二次型三、正交向量组的概念及求法1.定义5.1.3一组两两正交的非零向量称为正交向量组:若正交向量组中每个向量都是单位向量,则称该向量组为标准正交向量组例4 α1=(1,0,3)T,α2=(6,0,-2)T,α3=(0,1,0)T是正交向量组βi=(1,0,0)T,β2=(o,,) ,β3=(0,,-)是标准正交向量组
第五章 相似矩阵与二次型 1.定义5.1.3 一组两两正交的非零向量称为正交向量 组.若正交向量组中每个向量都是单位向量,则称该 向量组为标准正交向量组. 三、正交向量组的概念及求法 是正交向量组. 是标准正交向量组