第11章静电场 夕【例11=1】半径为R的半球面上均匀带电,带电量为Q。求圆心处的场强。 【解】我们先在半球面上取一细环,细环上的电荷 题图111 dR de-m d0 细环在轴线上产生的场强 6ow0-ee0eos6 dE=- 4E5R g-9me0=a 4x气R2 号【例1-2】在圆平面对称轴上有一点电荷0,9与圆平面的几何尺寸位置如图1-2a所 示。求:q的电力线穿过圆平面的通量。 毯性11-2利 您112, 阁11-c 【解】方法一:如图11-2b所示电力线穿过圆平面上细圆环ds的通量(在以下计算 过程中,应注意到图中x是常量。) dΦ=E5=cosod() ed0+ =
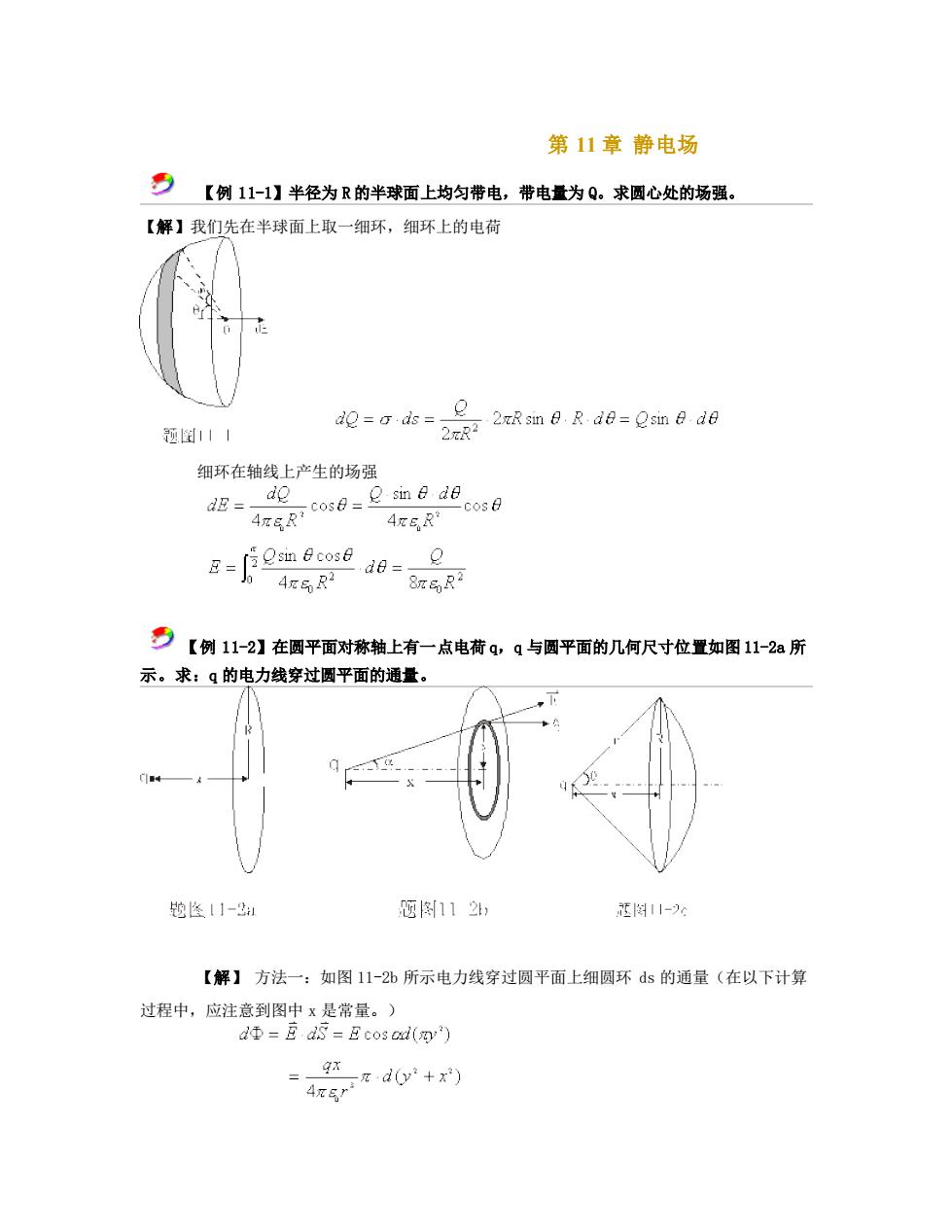
第 11 章 静电场 【例 11-1】半径为 R 的半球面上均匀带电,带电量为 Q。求圆心处的场强。 【解】我们先在半球面上取一细环,细环上的电荷 细环在轴线上产生的场强 【例 11-2】在圆平面对称轴上有一点电荷 q,q 与圆平面的几何尺寸位置如图 11-2a 所 示。求:q 的电力线穿过圆平面的通量。 【解】 方法一:如图 11-2b 所示电力线穿过圆平面上细圆环 ds 的通量(在以下计算 过程中,应注意到图中 x 是常量。)

=9x动 。T毁影 1 26 式中8如图c中所示。 方法二:如图c所示,穿过圆平面的电通量与穿过图示球冠的电通量相等。穿过包围点电荷q 闭合球面的总电量为8。,再由球冠面积S=2(一)占总球面面积4g中的比率,就可求 出球冠的电通量。由此求得圆平面的电通量: 枣s4×20y-=g1-5=号0-cos0 4 28。 ⊙【例11-3】一半径为的无限长带电圆柱体,其体电荷密度三%( P0为常数,”为离圆柱体轴线的距离。试求: (1)圆柱体内外各处的电场强度。 (2)求出场强最大值的位置在何处,场强多大? (3)求轴线处的电势。 【解】(1)如题图11-3所示,作高斯面5,由高斯定理 手g6=旦 (1) 高斯面内的9可通过体电荷积分求得: g-jp2or-jn吃点)2wt 2 代入(1)式: 题图11-8
式中 如图 c 中所示。 方法二:如图 c 所示,穿过圆平面的电通量与穿过图示球冠的电通量相等。穿过包围点电荷 q 闭合球面的总电量为 ,再由球冠面积 S=2 占总球面面积 中的比率,就可求 出球冠的电通量。由此求得圆平面的电通量: 【例 11-3】一半径为 的无限长带电圆柱体,其体电荷密度 ,其中 为常数, 为离圆柱体轴线的距离。试求: (1)圆柱体内外各处的电场强度。 (2)求出场强最大值的位置在何处,场强多大? (3)求轴线处的电势。 【解】(1)如题图 11-3 所示,作高斯面 S,由高斯定理 (1) 高斯面内的 可通过体电荷积分求得: 代入(1)式:

(2) 可见,当”<时,E为正,即沿半径方向向外 当’之@时,即圆柱体外场强为0 d祖=0 (2)场强最大的位置满足: dr 0--0 r= 得 3”处场强最大,代入(2)式得场强的最大值 18g (3)轴线处的电势 号【例1-4】一厚度水的无限大平板型区域中均匀分布着电荷,电荷体密度为。 (1)求板内外场强的分布,并画出场强分布曲线(), (2)若取中心面的电势为零,试求在意位置处的电势,并画出相应的电势分布曲线闭
(2) 可见,当 时, 为正,即沿半径方向向外 当 时,即圆柱体外场强为 0 (2)场强最大的位置满足: 即 得 处场强最大,代入(2)式得场强的最大值 (3)轴线处的电势 【例 11-4】一厚度为 的无限大平板型区域中均匀分布着电荷,电荷体密度为 。 (1)求板内外场强的分布,并画出场强分布曲线 ; (2)若取中心面的电势为零,试求任意位置处的电势,并画出相应的电势分布曲线