
第13章电介质 夕一、电极化强度 1、电极化强度是描述电介质极化强弱程度的物理量,定义单位为体积内分子电偶极矩的矢 量和,即: 2、电极化规律,电极化强度P与介质中的电场强度成正比,比例系数之:叫电极化率,各项 同性时户=无.6豆=(G-18豆 3、极化强度P与极化电荷面密度口的关系 g=P.=P=Pcos日 式中日为极化强度P与介质表面外法线方向的夹角。 两介质界面0=(月-)。 夕二、电介质中的高斯定理电位移矢量 1、高斯定理在有介质条件下的应用。 由真空中的高斯定理,在介质中考虑到极化电荷?的影响 f2a,+90 又 g'=手ps f(E+P5=∑g0 2、电位移矢量D 定义:0=+ 3、介质中的高斯定理 fDs=∑g0 引进电位移矢量D之后使介质中的高斯定理形式简化,闭合曲面的电位移通量只和自由电荷 9·有关,而与电介质的极化电荷无关。应注意极化电荷9(或极化强度户)的作用隐含在 电位移矢量D中,所以电位移矢量D既描述了介质中的场强E也描述了介质的极化。 4、各向同性均匀电介质充满电场所在空间,或各向同性均匀电介质的表面是等势面时,参 量D,豆,户等之间的相互关系。 由定义式 D=应+ 0-60+08-多 P=Xe6园 可得:
第 13 章 电介质 一、电极化强度 1、电极化强度是描述电介质极化强弱程度的物理量,定义单位为体积内分子电偶极矩的矢 量和,即: 。 2、电极化规律,电极化强度 与介质中的电场强度成正比,比例系数 叫电极化率,各项 同性时 3、极化强度 与极化电荷面密度 的关系 式中 为极化强度 与介质表面外法线方向的夹角。 两介质界面 二、电介质中的高斯定理 电位移矢量 1、高斯定理 在有介质条件下的应用。 由真空中的高斯定理,在介质中考虑到极化电荷 的影响 又 得 2、电位移矢量 定义: 3、介质中的高斯定理 引进电位移矢量 之后使介质中的高斯定理形式简化,闭合曲面的电位移通量只和自由电荷 有关,而与电介质的极化电荷无关。应注意极化电荷 (或极化强度 )的作用隐含在 电位移矢量 中,所以电位移矢量 既描述了介质中的场强 也描述了介质的极化。 4、各向同性均匀电介质充满电场所在空间,或各向同性均匀电介质的表面是等势面时,参 量 , , 等之间的相互关系。 由定义式 及 可得:

8=68, 8,=1+x ii 在上述条件下并且有 j=2= 京、夏 5、介质的击穿 在很强的电场作用下介质的绝缘性能会遭到破坏,这称为介质的击穿。某种介质能承受的最 大电场强度叫做击穿场强。 号三、电多的边值关系(在边界面上无自由电青的条件 1、电介质分界面两边电位移的法向分量相等,即 Du=Dis 2、电介质分解面两边电场强度的切向分量相等,即品:=B, g8-三= 3、电位移线的折射定律 g8, 夕四、电场的能量 1、点电荷的能量 1÷日g9, 或 或 ”号 2、电荷连续分布时的电能 对体电荷分布 理=n 对面电荷分布 W-[ais 3、电场的能量 W= 电场的能量密度 2s 五、各向同性介质中静电场量基本关系
在上述条件下并且有 5、介质的击穿 在很强的电场作用下介质的绝缘性能会遭到破坏,这称为介质的击穿。某种介质能承受的最 大电场强度叫做击穿场强。 三、电场的边值关系(在边界面上无自由电荷的条件下) 1、电介质分界面两边电位移的法向分量相等,即 2、电介质分解面两边电场强度的切向分量相等,即 3、电位移线的折射定律 四、电场的能量 1、点电荷的能量 或 或 2、电荷连续分布时的电能 对体电荷分布 对面电荷分布 3、电场的能量 电场的能量密度 五、各向同性介质中静电场量基本关系
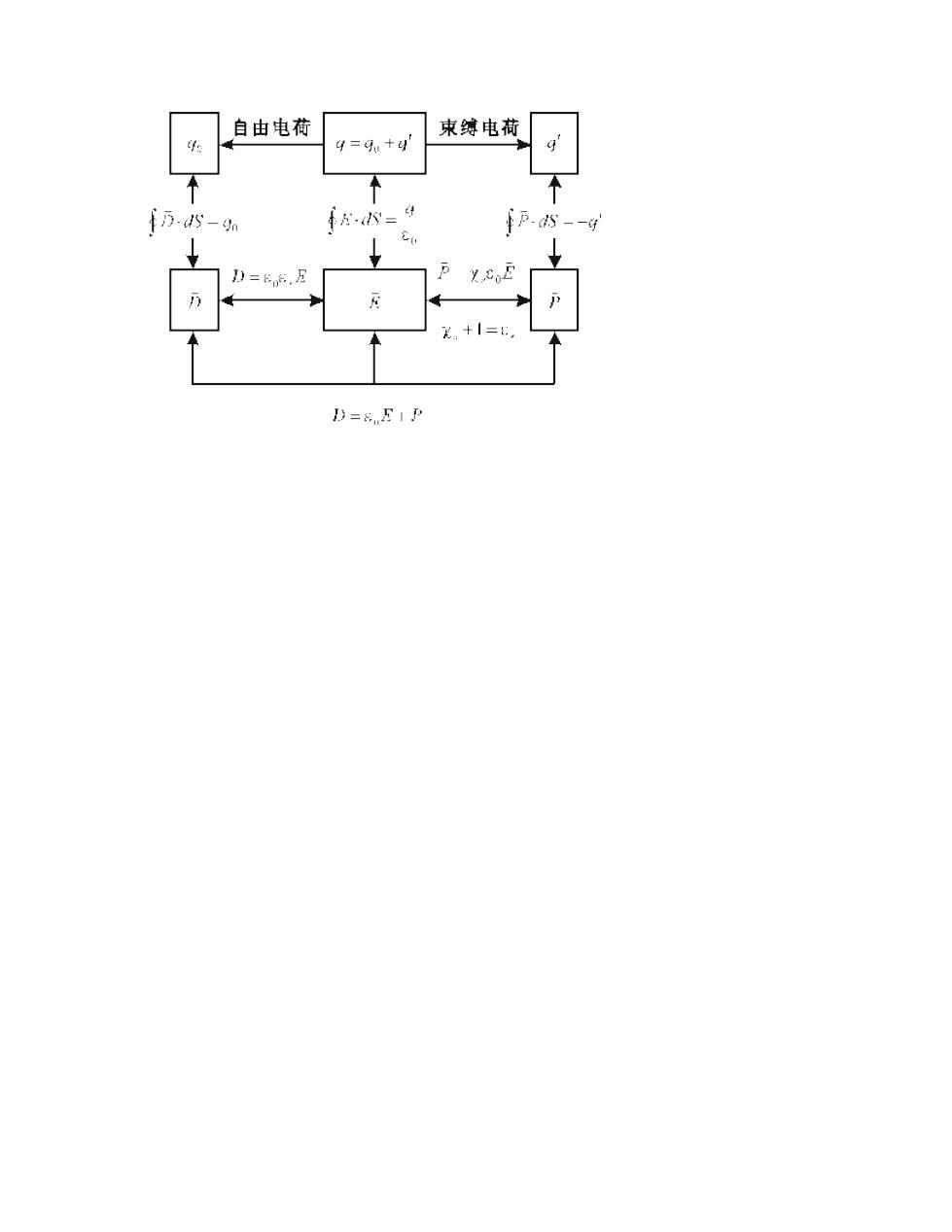
自由电荷 9=+g 束绮电荷 万- 千N= 4 .--g X.+1= D=8 EIP

第13章电介质 5 【例13-1】如题图13-1a所示平行板电容器,两板间距为。将它充电至电势差 为心,然后断开电源,插入2的相对介电常数为的电介质平板 (1)求电介质中的D,豆,户的大小及电介质表面的极化电荷'。 (2)求电容器两板板间的电势差; (3)画出电容器内的D线、豆线及P线: (4)如果在插入2电介质平板后,保持电源接通。那么电介质中的、豆、户又为多大? 西图131 【解】(1)插入电介质平板之前,电容器极板间的场强 8,因此 ⊙0三气d。虽然插入介质。由于已断开电源所以 豆、立,由介质中高斯定理可知 。=马豆不夜,由此我们可计续, D=00-60d 8=D 0_10 p=56-6-0g-54智 s.d Ey gB=g-1。 两d 插入介质板后两平行板间的电势差 8号号+是兰若
第 13 章 电介质 【例 13-1】如题图 13-1a 所示平行板电容器,两板间距为 。将它充电至电势差 为 ,然后断开电源,插入 的相对介电常数为 的电介质平板 (1)求电介质中的 , , 的大小及电介质表面的极化电荷 。 (2)求电容器两板板间的电势差; (3)画出电容器内的 线、 线及 线; (4)如果在插入 电介质平板后,保持电源接通。那么电介质中的 、 、 又为多大? 【解】(1)插入电介质平板之前,电容器极板间的场强 ,又 因此 。虽然插入介质。由于已断开电源所以 不变,由此我们可计算 、 、 ,由介质中高斯定理可知 插入介质板后两平行板间的电势差

红五古 - 城 g怪3-h (2)D线,豆线与户线如图b所示。 (3)由上面计算可知当断开电源在平行板电容器内插入介质后,电容器两板间电压下降了。 现在保持电源接通的情况下,电源对电容器就要充电。因此电容器两板上的自由电荷面密度 0就改变了。空气中的场强0也改变了,下面我们先计算在电源保持接通情况下的0。 2EU 得 8=1+8,)d 26n8,U 00=66= 由此: 1+s,)a D=8=8=1+5,a 2s6,U 2 U P=(g-0%8=s-12S g.+1d 夕【例13-2】设均匀极化的电介质球,极化强度为 (1)求极化电荷在球心处产生的场强。 (2)求证极化电荷在介质球内部产生的电场为均匀电场
(2) 线, 线与 线如图 b 所示。 (3)由上面计算可知当断开电源在平行板电容器内插入介质后,电容器两板间电压下降了。 现在保持电源接通的情况下,电源对电容器就要充电。因此电容器两板上的自由电荷面密度 就改变了。空气中的场强 也改变了,下面我们先计算在电源保持接通情况下的 。 得 由此: 【例 13-2】设均匀极化的电介质球,极化强度为 (1)求极化电荷在球心处产生的场强。 (2)求证极化电荷在介质球内部产生的电场为均匀电场