
第20章光的干涉和衍射 夕一、光的干涉条件 1、相干光的条件 (1)频率相同 (2)振动方向相同 (3)位相差 恒定 2、相干光的获得: 必须是同一光源分成二束或多束经过不同的路径再会聚才能满足相干条件。 3、干涉的明暗条件: (1)光程:1=x 光波在媒质中的几何路程换算成真空中的几何路程叫光程, (2)半波损失: 在入射角不太大的情况下,光波从光疏媒质()射向光密媒质(?),又从光密媒质反 射到光疏媒质时,相位改变?,相当于附加半个波长的光程叫做半波损失。除此之外的反射 光和透射光一般无半波损失。 (3)同一光源分成二束经过不同的光程?和1再会聚。该两束光的光程差: 以明条纹 =-=2+暗条纹 4、干涉条纹的可见度:(对比度) mx:+/am 式中为明条纹的最大光强,为暗条纹的最小光强 要使干涉条纹明显可见的补充条件: (1)被分成两束光的光源线度不能太大(空间相干性) (2)两束相干光之间的光程差不能太大(时间相干性) 最大光程差要小于相干长度, 式中孔为光源的平均波长,△入为谱线宽度 (3)两束相干光之间的光强相差不能太大。(可见度) 乡二、分波前的干涉:(单绪、双缝、多焦、光播的衍射与干涉)
第 20 章 光的干涉和衍射 一、光的干涉条件 1、相干光的条件: (1)频率相同 (2)振动方向相同 (3)位相差 恒定 2、相干光的获得: 必须是同一光源分成二束或多束经过不同的路径再会聚才能满足相干条件。 3、干涉的明暗条件: (1)光程: 光波在媒质中的几何路程换算成真空中的几何路程叫光程。 (2)半波损失: 在入射角 不太大的情况下,光波从光疏媒质( )射向光密媒质( ),又从光密媒质反 射到光疏媒质时,相位改变 ,相当于附加半个波长的光程叫做半波损失。除此之外的反射 光和透射光一般无半波损失。 (3)同一光源分成二束经过不同的光程 和 再会聚。该两束光的光程差: 4、干涉条纹的可见度:(对比度) 式中 为明条纹的最大光强, 为暗条纹的最小光强。 要使干涉条纹明显可见的补充条件: (1)被分成两束光的光源线度不能太大(空间相干性) (2)两束相干光之间的光程差不能太大(时间相干性) 最大光程差 要小于相干长度, 式中 为光源的平均波长, 为谱线宽度。 (3)两束相干光之间的光强相差不能太大。(可见度) 二、分波前的干涉:(单缝、双缝、多缝、光栅的衍射与干涉)

1、夫琅禾弗缝宽为a的单缝衍射光强分布的主要特点: (1)中央条纹(零级明条纹)的光强远大于其他各级明条纹。中央明条纹集中了大部分的 能量。 asm p=2K) (2)各级暗条纹的位置由 2 确定。 各级明条纹的近似位置为血=化+)子 式中2前系数2X,及2X+)即为单缝所分的半波带的数目 (3)中央明条纹的宽度: 4=2 (式中f为透镜的焦距) 各级明条纹的宽度 口约为中央明条纹宽度的一半。(在衍射角较小的条件 下) (4)单缝缝宽a越小,衍射越明显,光波波长越长,衍射越明显,白光通过单缝时出现 彩色条纹。 (5)单缝衍射的光强分布函数: 89m2asn日 1=1。 rasmn e 月2 th月@两8 光强分布如图所示 、④ . -0 A。0 图一序我北度均芳」4: 相应光强分布图位置0,①②③④处的光矢量A及相应和光强I的大小如下:
1、夫琅禾弗缝宽为 a 的单缝衍射光强分布的主要特点: (1)中央条纹(零级明条纹)的光强远大于其他各级明条纹。中央明条纹集中了大部分的 能量。 (2)各级暗条纹的位置由 确定。 各级明条纹的近似位置为 式中 前系数 ,及 即为单缝所分的半波带的数目。 (3)中央明条纹的宽度: (式中 f 为透镜的焦距) 各级明条纹的宽度 约为中央明条纹宽度的一半。(在衍射角较小的条件 下) (4)单缝缝宽 a 越小,衍射越明显,光波波长 越长,衍射越明显,白光通过单缝时出现 彩色条纹。 (5)单缝衍射的光强分布函数: 式中 光强分布如图所示。 相应光强分布图位置 0,①②③④处的光矢量 及相应 和光强 I 的大小如下:
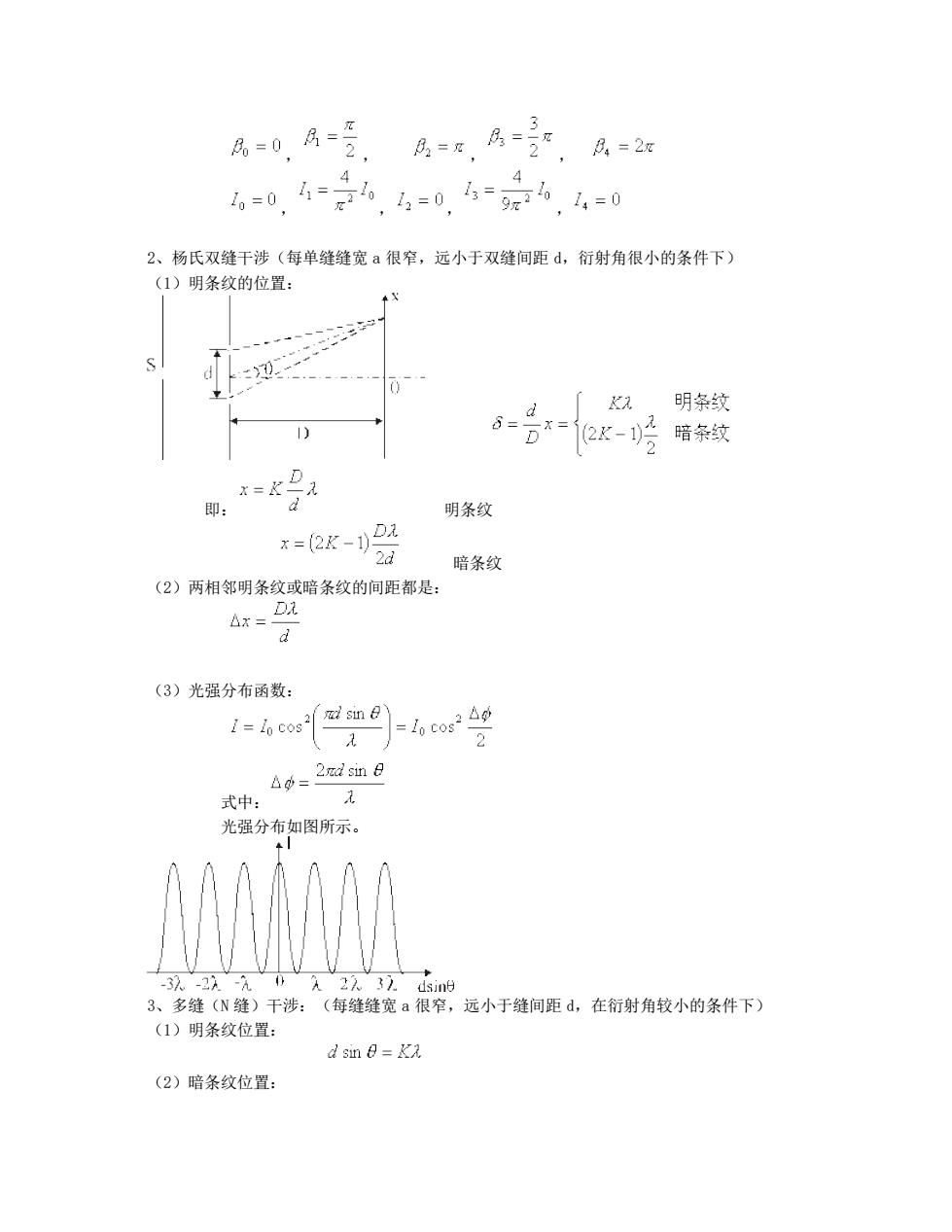
月=0月= , 房=8.月=”,风=2 =0.4=6.=0.4=6,4=0 2、杨氏双缝干涉(每单缝缝宽a很窄,远小于双缝间距d,衍射角很小的条件下) (1)明条纹的位置: d 明条纹 ) 6=Dx=2-岭暗条纹 即: 明条纹 x=2x-1)2 2d 暗条纹 (2)两相邻明条纹或暗条纹的间距都是: △x= DA (3)光强分布函数: I-hcosmm 2 4=2dm日 式中: 光强分布如图所示。 A -37-2A-A A2232.5im的 3、多缝(N缝)干涉:(每缝缝宽a很窄,远小于缝间距d,在衍射角较小的条件下) (1)明条纹位置: dsm日=K (2)暗条纹位置:
, , , , , , , , 2、杨氏双缝干涉(每单缝缝宽 a 很窄,远小于双缝间距 d,衍射角很小的条件下) (1)明条纹的位置: 即: 明条纹 暗条纹 (2)两相邻明条纹或暗条纹的间距都是: (3)光强分布函数: 式中: 光强分布如图所示。 3、多缝(N 缝)干涉:(每缝缝宽 a 很窄,远小于缝间距 d,在衍射角较小的条件下) (1)明条纹位置: (2)暗条纹位置:

dm- (i<W) 右N-1个暗占 (3)有N-2个次极大,位置近似在两暗点中间,次级大的光强远小于主极大光强。 (4)光强分布函数: I=lo- 2如=, 2 46=2dm日 式中: N=6时的光强分布如图所示。 4、光栅(N很大时的多缝干涉) (1)光栅常数 d=a+0 “为通光部分的宽度、b为不通光部分的宽度。 (2)光强分布的主要特点: 明条纹位置:白+)m日= 明条纹细而明亮,次明条纹相对很暗,因此背景几乎一片黑暗。光强分布图类似于 六缝的光强分布。当缝数N很大时,次明几乎看不见了,明条纹更细更亮。 (3)光栅的分辨本领: 瑞利准则:波长为的光第K级明条纹恰好落在波长+△的K级相邻的第一暗级 R=乙 位置时,我们认为恰好认为能够分辨这两条谱线。分辨本领定义为: 光桶的分辨本领为: 式中N为光栅的狭缝的总数,狭缝总数N越大,干涉条纹越细越明亮。 式中K为干涉条纹的级项,K越大,无和入+△入两谱线分得越开。 5、单缝衍射对双缝及多缝干涉的影响 (1)干涉和衍射的相互关系: 干涉和衍射并无实质性的物理差别,只是所谓干涉是指有限波的迭加结果,而衍射指衍射波 波面上无数子波的迭加结果,其本质仍然是干涉。干涉和衍射都产生明暗相间的条纹,但条 纹的分布和光强的分布不相同。无论是双缝还是光橱干涉都受到每一单缝衍射的影响,其条
( ) 有 N-1 个暗点。 (3)有 N-2 个次极大,位置近似在两暗点中间,次级大的光强远小于主极大光强。 (4)光强分布函数: 式中: N=6 时的光强分布如图所示。 4、光栅(N 很大时的多缝干涉) (1)光栅常数 为通光部分的宽度、 为不通光部分的宽度。 (2)光强分布的主要特点: 明条纹位置: 明条纹细而明亮,次明条纹相对很暗,因此背景几乎一片黑暗。光强分布图类似于 六缝的光强分布。当缝数 N 很大时,次明几乎看不见了,明条纹更细更亮。 (3)光栅的分辨本领: 瑞利准则:波长为 的光第 K 级明条纹恰好落在波长 的 K 级相邻的第一暗级 位置时,我们认为恰好认为能够分辨这两条谱线。分辨本领定义为: 。 光栅的分辨本领为: 。 式中 N 为光栅的狭缝的总数,狭缝总数 N 越大,干涉条纹越细越明亮。 式中 K 为干涉条纹的级项,K 越大, 和 两谱线分得越开。 5、单缝衍射对双缝及多缝干涉的影响 (1)干涉和衍射的相互关系: 干涉和衍射并无实质性的物理差别,只是所谓干涉是指有限波的迭加结果,而衍射指衍射波 波面上无数子波的迭加结果,其本质仍然是干涉。干涉和衍射都产生明暗相间的条纹,但条 纹的分布和光强的分布不相同。无论是双缝还是光栅干涉都受到每一单缝衍射的影响,其条

纹都是衍射和干涉两者结合的结果,干涉光强受到衍射光强的调制。 (2)单缝衍射对双缝干涉的调制作用: 双缝中每一缝缝宽为4,每一单缝产生的衍射光强分布: sm2月 双缝间距为,双缝间干涉的光强分布: 1=4co24=4,mcog2△=nm 2 82 c0s240 8=sin 式中: 40=2dsm日 图示为单缝衍射对双缝调制总光强的分布(图中虚线为单缝衍射因子所形成的包络线)。 (3)单缝衍射对多缝(或光橱)的调制作用 单缝衍射因子对N缝干涉调制后的总光强分布函数 2 sim20 82 式中: 4=2a+)m8 图示为单缝衍射对六缝调制后的光强分布(图中虚线为单缝衍射因子所形成的包络线) (4)缺级问题: 当多缝干涉(包括双缝、光栅)的明条纹位置: (a+b)sin 0=KA 与单缝衍射的暗条纹位置:
纹都是衍射和干涉两者结合的结果,干涉光强受到衍射光强的调制。 (2)单缝衍射对双缝干涉的调制作用: 双缝中每一缝缝宽为 ,每一单缝产生的衍射光强分布: 双缝间距为 ,双缝间干涉的光强分布: 式中: ; 图示为单缝衍射对双缝调制总光强的分布(图中虚线为单缝衍射因子所形成的包络线)。 (3)单缝衍射对多缝(或光栅)的调制作用 单缝衍射因子对 N 缝干涉调制后的总光强分布函数: 式中: ; ; 图示为单缝衍射对六缝调制后的光强分布(图中虚线为单缝衍射因子所形成的包络线)。 (4)缺级问题: 当多缝干涉(包括双缝、光栅)的明条纹位置: 与单缝衍射的暗条纹位置: