
第2章质点动力学 一、质点 是物体的理想模型。它只有质量而没有大小。平动物体可作为质点运动来处理,或物体的形 状大小对物体运动状态的影响可忽略不计是也可近似为质点。 9三、力: 是物体间的相互作用。分为接触作用与场作用。在经典力学中,场作用主要为万有引力(重 力),接触作用主要为弹性力与摩擦力。 1、弹性力:F=- (x为形变量) 2、摩擦力:摩擦力的方向永远与相对运动方向(或趋势)相反。 固体间的静摩擦力:了=4W (最大值) 固体间的滑动摩擦力:大=4,N 3、流体阻力:了=-bv或了=-cu =GMin 4、万有引力: GMi 特例:在地球引力场中,在地球表面附近: F-R-ME 式中R为地球半径,M为地球质量。 在地球上方(”较大), 在地球内部(<R), P=州8R 号三、债性参考系中的力学提律牛顿三定排 牛顿第一定律:户=0时,=恒矢量。牛顿第一定律阐明了惯性与力的概念,定义了惯 性系。 牛顿第二定律: 方=dw) 普遍形式: d 经典形式: (m为恒量) 牛顿第三定律:月。=-瓦
第 2 章 质点动力学 一、质点: 是物体的理想模型。它只有质量而没有大小。平动物体可作为质点运动来处理,或物体的形 状大小对物体运动状态的影响可忽略不计是也可近似为质点。 二、力: 是物体间的相互作用。分为接触作用与场作用。在经典力学中,场作用主要为万有引力(重 力),接触作用主要为弹性力与摩擦力。 1、弹性力: ( 为形变量) 2、摩擦力:摩擦力的方向永远与相对运动方向(或趋势)相反。 固体间的静摩擦力: (最大值) 固体间的滑动摩擦力: 3、流体阻力: 或 。 4、万有引力: 特例:在地球引力场中,在地球表面附近: 。 式中 R 为地球半径,M 为地球质量。 在地球上方( 较大), 。 在地球内部( ), 。 三、惯性参考系中的力学规律 牛顿三定律 牛顿第一定律: 时, 。牛顿第一定律阐明了惯性与力的概念,定义了惯 性系。 牛顿第二定律: 普遍形式: ; 经典形式: ( 为恒量) 牛顿第三定律:

牛顿运动定律是物体低速运动(U<C)时所遵循的动力学基本规律,是经典力学的基 础。 乡 四、非惯性参考系中的力学规律 1、惯性力: 京=-ma-a)- ”→平移加速系疗=一d, →匀速转动系豆=-mm节,(@=0) 惯性力没有施力物体,因此它也不存在反作用力。但惯性力同样能改变物体相对于参考系的 运动状态,这体现了惯性力就是参考系的加速度效应。 2、引入惯性力后,非惯性系中力学规律:F+云=m 号五、泉桥动力学日愚的主要步 恒力作用下的连接体约束运动:选取研究对象,分析运动趋势,画出隔离体示力图,列出分 量式的运动方程。 变力作用下的单质点运动:分析力函数,选取坐标系,列运动方程,用积分法求解
牛顿运动定律是物体低速运动( )时所遵循的动力学基本规律,是经典力学的基 础。 四、非惯性参考系中的力学规律 1、惯性力: 惯性力没有施力物体,因此它也不存在反作用力。但惯性力同样能改变物体相对于参考系的 运动状态,这体现了惯性力就是参考系的加速度效应。 2、引入惯性力后,非惯性系中力学规律: 五、求解动力学问题的主要步骤 恒力作用下的连接体约束运动:选取研究对象,分析运动趋势,画出隔离体示力图,列出分 量式的运动方程。 变力作用下的单质点运动:分析力函数,选取坐标系,列运动方程,用积分法求解

第2章质点动力学 夕二、解题示例 【例2-1】如题图2-1a所示一倾角为的斜面放在水平面上,斜面上放一木块,两者 间摩擦系数为4<g⊙)。为使木块相对斜面静止,求斜面加速度的范围。 m --ra mg 题21b y 题21a 题21c 【解】方法一我们如b图取坐标,并假设物体有下滑趋势,根据受力图可列出动力学方 2Nsm-fcos8=ma Ncos日+fsm日-g=0 这样两个方程两个未知数,可解,但解的过程较繁。若将坐标轴分别沿斜面和斜面垂直方法上 取,使得一个未知力与一个坐标轴垂直,使得在一个方向上的方程中只出现一个未知力,这样 一个方程就能独立地解出一个未知力来了。如图c所示可列出如下牛顿动力学方程: x方向 mg sin e-f=macose y方向 N-gcos日=masm日 由此解得 f=wgsm日-macos日 N=mg cos e+masine 由相对静止条件要求 -W≤f≤國 可解得加速度a的范围为:
第 2 章 质点动力学 二、解题示例 【例 2-1】如题图 2-1a 所示一倾角为 的斜面放在水平面上,斜面上放一木块,两者 间摩擦系数为 。为使木块相对斜面静止,求斜面加速度 的范围。 【解】方法一 我们如 b 图取坐标,并假设物体有下滑趋势,根据受力图可列出动力学方 程: 这样两个方程两个未知数,可解,但解的过程较繁。若将坐标轴分别沿斜面和斜面垂直方法上 取,使得一个未知力与一个坐标轴垂直,使得在一个方向上的方程中只出现一个未知力,这样 一个方程就能独立地解出一个未知力来了。如图 c 所示可列出如下牛顿动力学方程: x 方向 y 方向 由此解得 由相对静止条件要求 可解得加速度 的范围为:
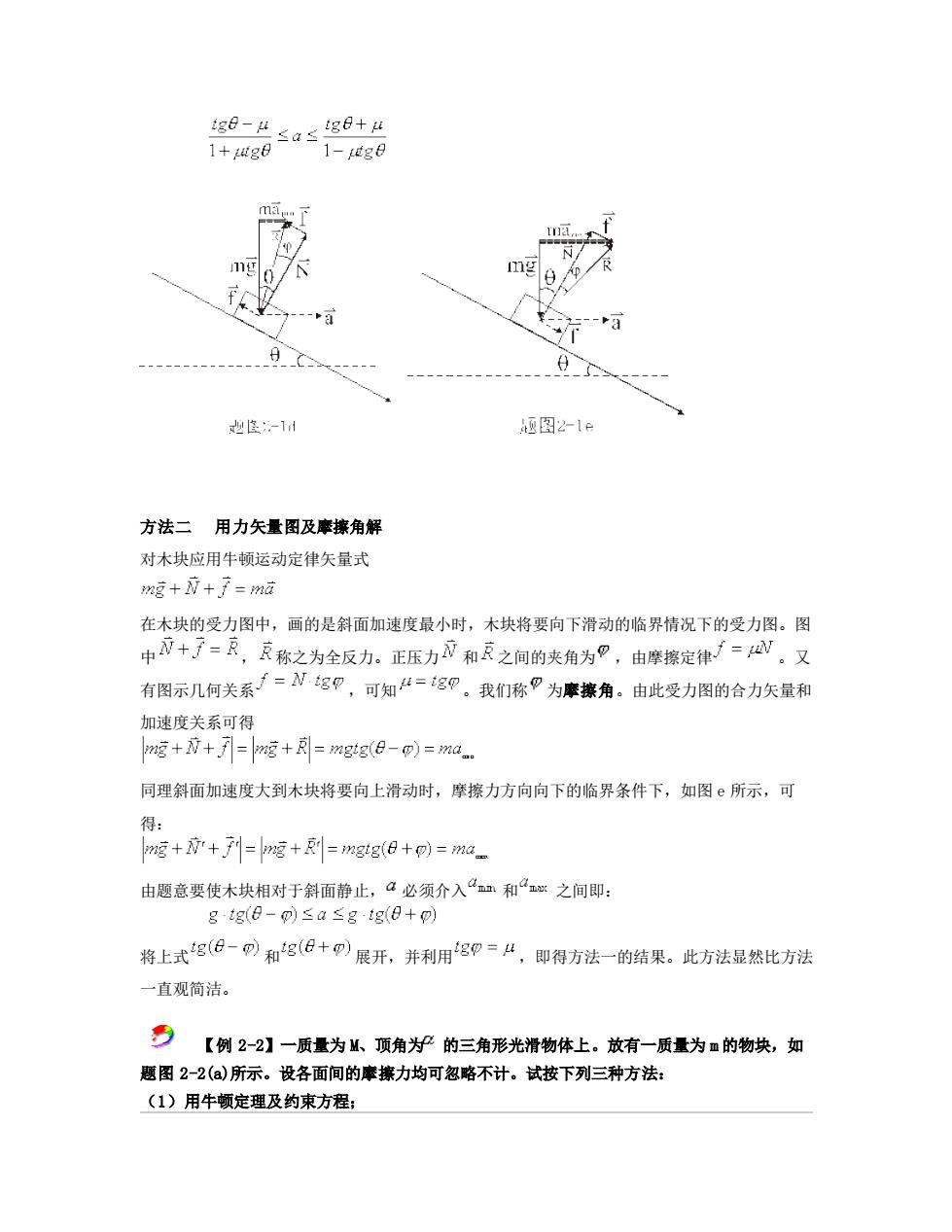
tg8-4 1+g8 sas ige+u 1-g日 ma 起退女1d @图21e 方法二用力矢量图及摩擦角解 对木块应用牛顿运动定律矢量式 w落+衣+了=m这 在木块的受力图中,画的是斜面加速度最小时,木块将要向下滑动的临界情况下的受力图。图 中+了=瓦,反称之为全反力.正压力衣和反之间的夹角为巴,由摩擦定律=V。又 有图示几何关系了=NgP,可知“=g9。我们称P为摩擦角。由此受力图的合力矢量和 加速度关系可得 g++=馆+=mgge-)=ma. 同理斜面加速度大到木块将要向上滑动时,摩擦力方向向下的临界条件下,如图©所示,可 得: 9馆+7r+升=g+利=mgg(6+)=a 由题意要使木块相对于斜面静止,a必须介入a和之间即: gge-网≤a≤gtg(e+ 将上式38-网和3(8+网展开,并利用89=“,即得方法一的结果。此方法显然比方法 一直观简洁。 号【倒2-2】一质量为以、顶角为的三角形光滑物体上。放有一质量为■的物块,如 题图2-2()所示。设各面间的率擦力均可忽略不计。试按下列三种方法: (1)用牛顿定理及约束方程:
方法二 用力矢量图及摩擦角解 对木块应用牛顿运动定律矢量式 在木块的受力图中,画的是斜面加速度最小时,木块将要向下滑动的临界情况下的受力图。图 中 , 称之为全反力。正压力 和 之间的夹角为 ,由摩擦定律 。又 有图示几何关系 ,可知 。我们称 为摩擦角。由此受力图的合力矢量和 加速度关系可得 同理斜面加速度大到木块将要向上滑动时,摩擦力方向向下的临界条件下,如图 e 所示,可 得: 由题意要使木块相对于斜面静止, 必须介入 和 之间即: 将上式 和 展开,并利用 ,即得方法一的结果。此方法显然比方法 一直观简洁。 【例 2-2】一质量为 M、顶角为 的三角形光滑物体上。放有一质量为 m 的物块,如 题图 2-2(a)所示。设各面间的摩擦力均可忽略不计。试按下列三种方法: (1)用牛顿定理及约束方程;
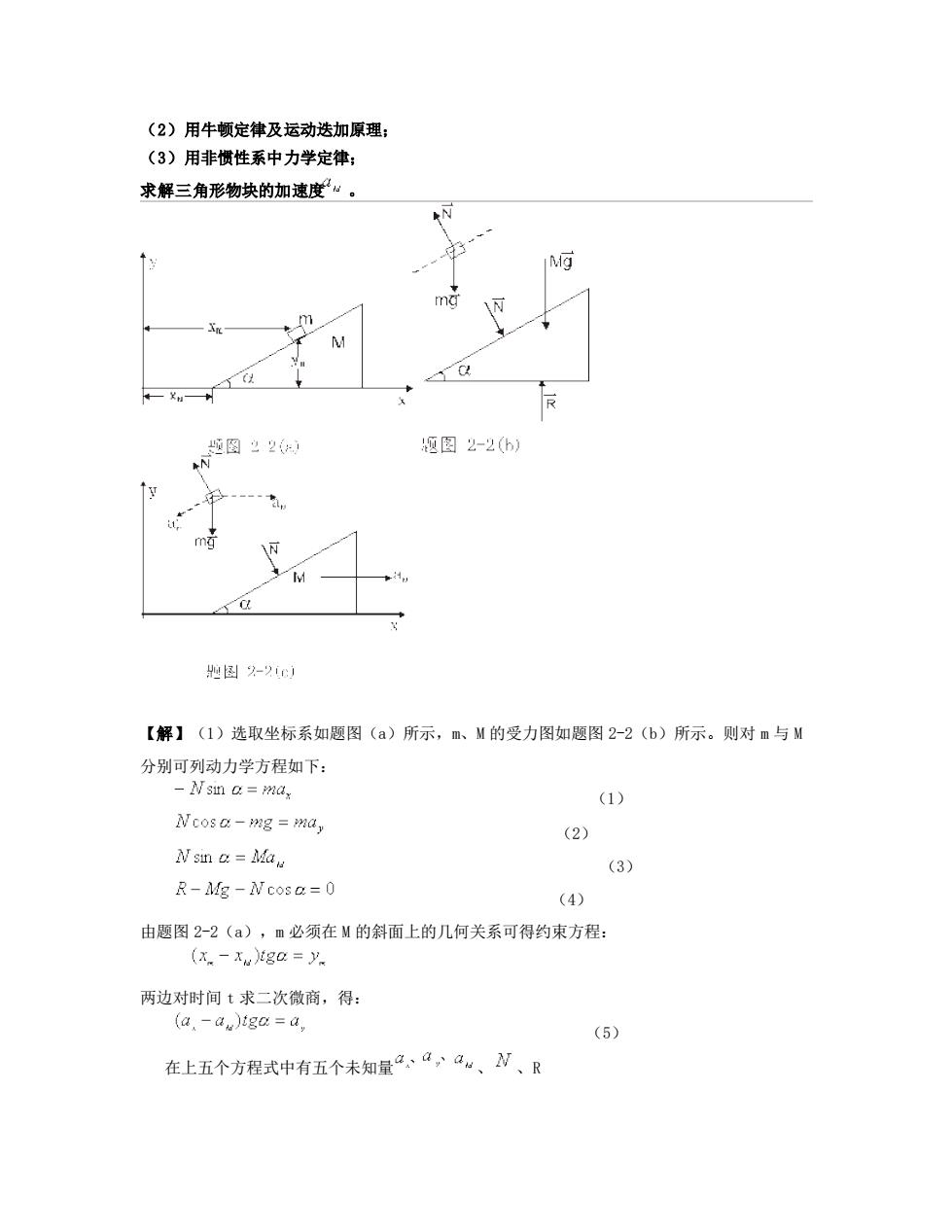
(2)用牛顿定律及运动迭加原理: (3)用非惯性系中力学定律; 求解三角形物块的加速度“。 N +N型图2 题图2-2(6) 担图-cd 【解】(1)选取坐标系如题图()所示,m、M的受力图如题图2-2(b)所示。则对m与M 分别可列动力学方程如下: -N sin a=ma (1) Ncosa-mg=mdy (2) Nsim a=May (3) R-Mg-Ncosa=0 (4) 由题图2-2(a),m必须在M的斜面上的几何关系可得约束方程: (x.-xuiga=y. 两边对时间t求二次微商,得 (a.-d)iga=a, (5) 在上五个方程式中有五个未知量4,“,a。、N、R
(2)用牛顿定律及运动迭加原理; (3)用非惯性系中力学定律; 求解三角形物块的加速度 。 【解】(1)选取坐标系如题图(a)所示,m、M 的受力图如题图 2-2(b)所示。则对 m 与 M 分别可列动力学方程如下: (1) (2) (3) (4) 由题图 2-2(a),m 必须在 M 的斜面上的几何关系可得约束方程: 两边对时间 t 求二次微商,得: (5) 在上五个方程式中有五个未知量 、 、R