
第19章光的偏振 夕一、原子发光模型 原子是物质发光的基元。原子中每次能级跃迁发射一个有限长的电磁横波波列,各波列互不 相干。 夕二、自然光和偏振光 1、自然光:光线上任一点的豆矢量的振动,在垂直于波速的平面上的各个方向上出现几率 均等的光称为自然光。自然光的三矢量可以看作两个互相垂直而振幅相等的独立的(指无相 位关系)分振动。 2、偏振光:光线上各点的豆矢量都在同一平面内,或沿着同一固定方向振动的光,称为偏 振光。由于豆矢量均在其振动方向和传播方向所构成的平面一一振动平面内,故称为平面偏 振光:当对着光线的传播方向观察时,由于豆矢量的振动方向为一直线,故也称为线偏振 光。 夕三、马吕斯定律 光强为。的线偏振光,通过检偏振器后透射光的强度为: 1=l0cos'a 式中口为起偏振化方向与检偏振器的偏振化方向之夹角, 号四、布僵斯袋定律: 反射光偏振化程度决定于入射角,当满足 时,反射光为完全偏振 光,振动方向垂直于入射面。此时记为0。 对于折射光,无论入射角?为何值,都是部分偏振光
第 19 章 光的偏振 一、原子发光模型 原子是物质发光的基元。原子中每次能级跃迁发射一个有限长的电磁横波波列,各波列互不 相干。 二、自然光和偏振光 1、自然光:光线上任一点的 矢量的振动,在垂直于波速的平面上的各个方向上出现几率 均等的光称为自然光。自然光的 矢量可以看作两个互相垂直而振幅相等的独立的(指无相 位关系)分振动。 2、偏振光:光线上各点的 矢量都在同一平面内,或沿着同一固定方向振动的光,称为偏 振光。由于 矢量均在其振动方向和传播方向所构成的平面——振动平面内,故称为平面偏 振光;当对着光线的传播方向观察时,由于 矢量的振动方向为一直线,故也称为线偏振 光。 三、马吕斯定律 光强为 的线偏振光,通过检偏振器后透射光的强度为: 式中 为起偏振化方向与检偏振器的偏振化方向之夹角。 四、布儒斯特定律: 反射光偏振化程度决定于入射角 ,当 满足 时,反射光为完全偏振 光,振动方向垂直于入射面。此时 记为 。 对于折射光,无论入射角 为何值,都是部分偏振光

夕五、光的双折射 1、双折射现象:当光线进入某类晶体(如方解石),其折射光线分裂为两束(寻常光0和 非常光),沿不同方向传播的现象称为光的双折射, 2、寻常光o和非常光e 0光:遵守折射定律,对于确定的晶体,各方向的折射率为恒量,。光的振动方向垂直 于光轴。 e光:不遵守折射定律,折射率”:的量值与方向有关,仅在光轴方向其折射率才与0 光相等。它的振动方向与光轴在同一平面内。 夕六、精质(成圆〕负报光 1、椭圆(或圆)偏振光: 豆矢量在每一瞬间时只有一个振动面。若该振动面不随时间变化,则为上述的平面偏振光, 若该振动面随时间而旋转,则当E矢量的端点描绘一个椭圆时,为椭圆偏振光:当豆矢量的 端点描绘一圆时,为圆偏振光。 2、椭圆偏振光和圆偏振光的获得 线偏振光垂直入射于光轴平行的晶面,若其振动面与光轴成口角时,便可分解为两振动面, 振动面与光轴垂直的为0光,振动面在光轴平面内的为e光。通过厚度为d的晶片后,0光 与0光的光程差5=,d-”4。由振动方向相互垂直的振动合成规律可得: 当 时,获得线偏振光: 当△0≠c时,获得椭圆偏振光,当口=4行时,获得圆偏振光
五、光的双折射 1、双折射现象:当光线进入某类晶体(如方解石),其折射光线分裂为两束(寻常光 o 和 非常光 e),沿不同方向传播的现象称为光的双折射。 2、寻常光 o 和非常光 e o 光:遵守折射定律,对于确定的晶体,各方向的折射率 n 为恒量,o 光的振动方向垂直 于光轴。 e 光:不遵守折射定律,折射率 的量值与方向有关,仅在光轴方向其折射率才与 o 光相等。它的振动方向与光轴在同一平面内。 六、椭圆(或圆)偏振光 1、椭圆(或圆)偏振光: 矢量在每一瞬间时只有一个振动面。若该振动面不随时间变化,则为上述的平面偏振光, 若该振动面随时间而旋转,则当 矢量的端点描绘一个椭圆时,为椭圆偏振光;当 矢量的 端点描绘一圆时,为圆偏振光。 2、椭圆偏振光和圆偏振光的获得 线偏振光垂直入射于光轴平行的晶面,若其振动面与光轴成 角时,便可分解为两振动面, 振动面与光轴垂直的为 o 光,振动面在光轴平面内的为 e 光。通过厚度为 d 的晶片后,o 光 与 e 光的光程差 。由振动方向相互垂直的振动合成规律可得: 当 时,获得线偏振光; 当 时,获得椭圆偏振光,当 时,获得圆偏振光

第19章光的偏振 夕【例19-1】有一厚为0.2m的石英晶片,它的折射率,=154,点=1553,间 这晶片对球些可见光是波片?哪些可见光是2波片? 【解】由四分之一波片的定义是o光与e光通过该波片后的光程差满足: 以=以+号 应该注意在这种情况下不要忽略了K入这一项, 2=,-%,2-1553-1549x2×10÷18×10-6 名+4 +025 K+025 在可见光400m~760m范围内K只能取3和4, 3所,名=18x10 -=5542 2,=18×10 4.25 .=42422 3.25 K=4时: 对二分之一波片而言应满足: =-%18×10 0-%妞=a+2 + K+0.5 即: 在可见光范围内K只取2,3,4 18x10 =720 当K=2时 25 飞=18×10 =5142w 当K=3时 35 ,18x10 =400m 当K=4时 45 所以这晶片可作为54,424%的4波片,可作720”、514%m及400m的半波 片。 号【例19-2】试分析线偏振光通过几种不同情况下的波片后的偏叛态。 【解】先回顾两个频率相同振动方向相互垂直振动的合成: 两谐振动方程分别为: x=A cos ad y=A coslat+o)
第 19 章 光的偏振 【例 19-1】有一厚为 0.2mm 的石英晶片,它的折射率 , ,问 这晶片对哪些可见光是 波片?哪些可见光是 波片? 【解】由四分之一波片的定义是 o 光与 e 光通过该波片后的光程差满足: 应该注意在这种情况下不要忽略了 这一项, 在可见光 ~ 范围内 K 只能取 3 和 4, K=3 时: ; K=4 时: 对二分之一波片而言应满足: 即: 在可见光范围内 K 只取 2,3,4 当 K=2 时 当 K=3 时 当 K=4 时 所以这晶片可作为 , 的 波片,可作 、 及 的半波 片。 【例 19-2】试分析线偏振光通过几种不同情况下的波片后的偏振态。 【解】先回顾两个频率相同振动方向相互垂直振动的合成: 两谐振动方程分别为:
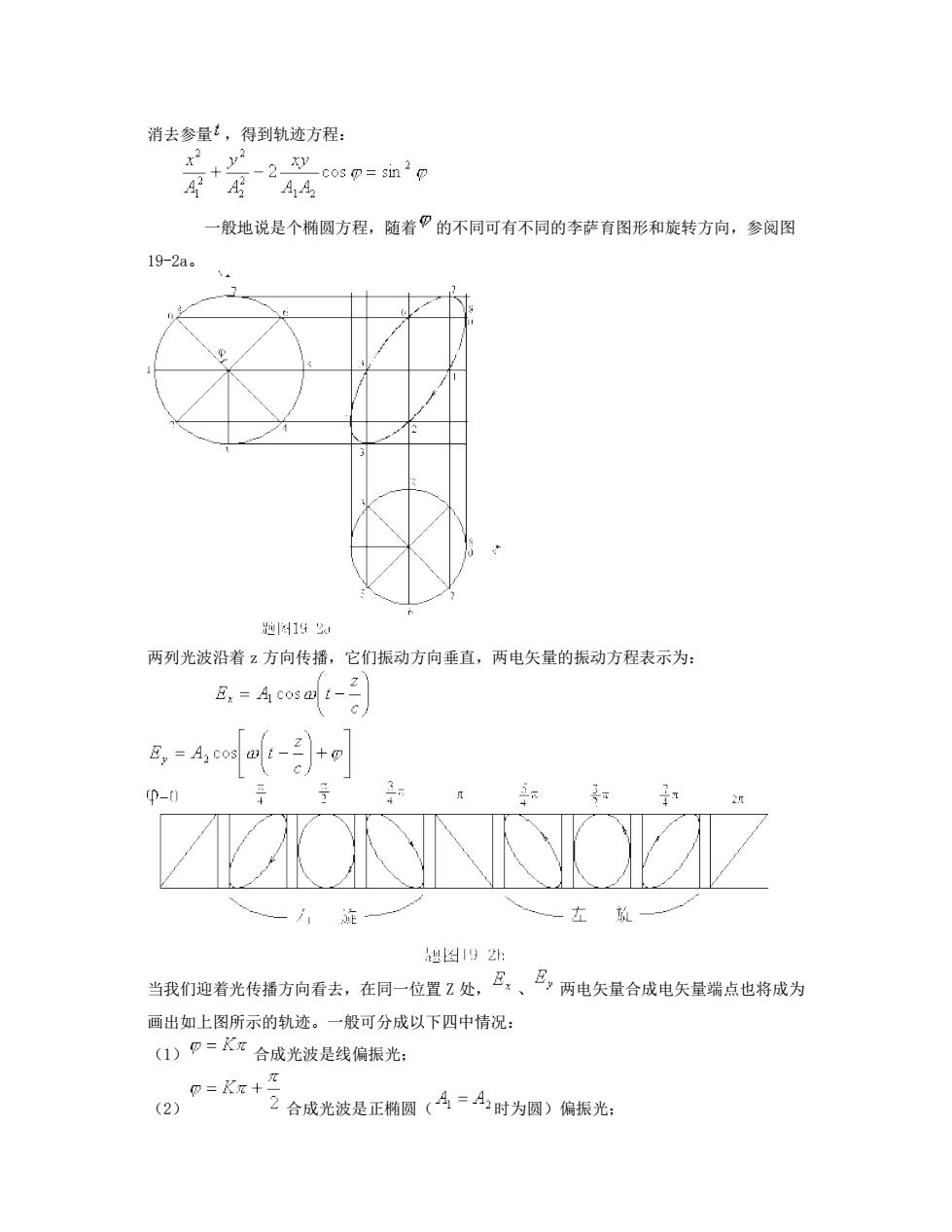
消去参量,得到轨迹方程: 3 厚+再244cos0=mp 一般地说是个椭圆方程,随着”的不同可有不同的李萨育图形和旋转方向,参阅图 19-2a. 抛1a 两列光波沿着z方向传播,它们振动方向垂直,两电矢量的振动方程表示为: p-0 左 进图192 当我们迎着光传播方向看去,在同一位置Z处,巴,、,两电矢量合成电矢量端点也将成为 画出如上图所示的轨迹。一般可分成以下四中情况: (1)=K灯合成光波是线偏振光: D=Kg+ (2) 2合成光波是正椭圆(A=A时为圆)偏振光
消去参量 ,得到轨迹方程: 一般地说是个椭圆方程,随着 的不同可有不同的李萨育图形和旋转方向,参阅图 19-2a。 两列光波沿着 z 方向传播,它们振动方向垂直,两电矢量的振动方程表示为: 当我们迎着光传播方向看去,在同一位置 Z 处, 、 两电矢量合成电矢量端点也将成为 画出如上图所示的轨迹。一般可分成以下四中情况: (1) 合成光波是线偏振光; (2) 合成光波是正椭圆( 时为圆)偏振光;
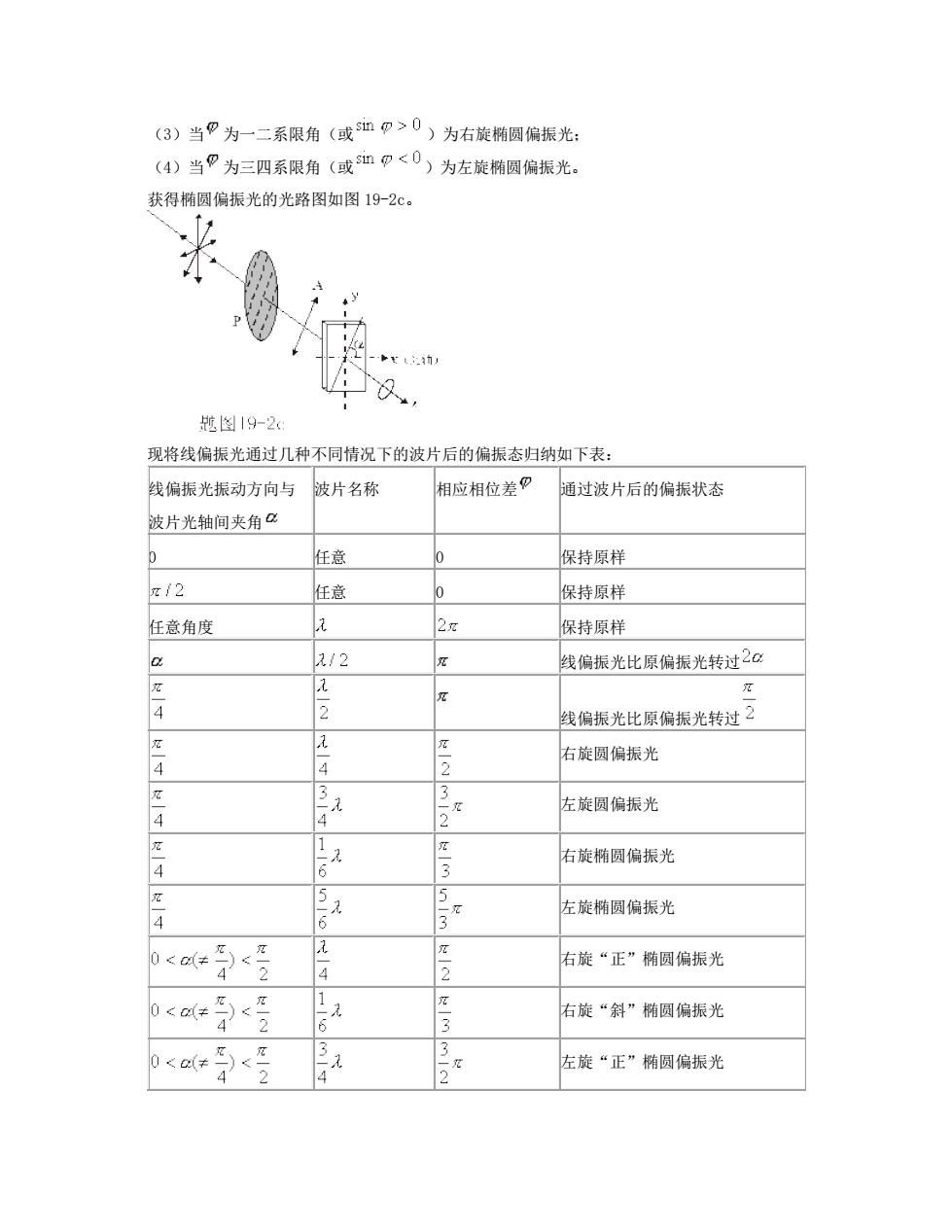
(3)当?为一二系限角(或血p>0)为右旋椭圆偏振光: (4)当”为三四系限角(或出P<0)为左旋椭圆偏振光。 获得椭圆偏振光的光路图如图19-2c。 越图19-2( 现将线偏振光通过几种不同情况下的波片后的偏振态归纳如下表: 线偏振光振动方向与 波片名称 相应相位差? 通过波片后的偏振状态 波片光轴间夹角a D 任意 保持原样 :12 任意 保持原样 任意角度 死 保持原样 a 12 线偏振光比原偏振光转过2a 2 线偏振光比原偏振光转过2 右旋圆偏振光 4 左旋圆偏振光 右旋椭圆偏振光 左旋椭圆偏振光 2 4 右旋“正”椭圆偏振光 右旋“斜”椭圆偏振光 2 2 左旋“正”椭圆偏振光
(3)当 为一二系限角(或 )为右旋椭圆偏振光; (4)当 为三四系限角(或 )为左旋椭圆偏振光。 获得椭圆偏振光的光路图如图 19-2c。 现将线偏振光通过几种不同情况下的波片后的偏振态归纳如下表: 线偏振光振动方向与 波片光轴间夹角 波片名称 相应相位差 通过波片后的偏振状态 0 任意 0 保持原样 任意 0 保持原样 任意角度 保持原样 线偏振光比原偏振光转过 线偏振光比原偏振光转过 右旋圆偏振光 左旋圆偏振光 右旋椭圆偏振光 左旋椭圆偏振光 右旋“正”椭圆偏振光 右旋“斜”椭圆偏振光 左旋“正”椭圆偏振光