
第22章量子力学基础 夕一、德布罗意物质波 德布罗意认为不仅光具有波粒二象性,实物粒子也具有波粒二象性。描述实物粒子波函数中 的Y、元与实物粒子的能量E和动量D的德布罗意关系: =hv 戴维孙一革末电子衍射实验,约恩孙电子双缝干涉实验都证实了电子具有的波动性。 夕二、海森伯不确定关系 由于微观粒子具有波粒二象性,我们就无法同时精确地测定微观粒子坐标与动量,海森伯提 出了如下的不确定关系: 1、动量-坐标不确定关系 x,≥为 bybp,2h △2.22 2、时间-能量不确定关系 △E-At2h 号三、被数y2 微观粒子具有波粒二象性,它不同于经典的波也不同于经典的粒子,要描述微观粒子群体随 时间的变化,引入波函数。波函数确定后,微观粒子的波粒二象性就能得到准确的描述。波 函数是微观粒子的态函数。 1、波函数的物理意义: 某一时刻在空间某一位置粒子出现的几率正比于该时刻该位置波函数的平方,或 gv=,即 几率密度 p(x.y.2.t)=(x.y.2.) 2、波函数的归一化条件 ∬°w=1 3、波函数的标准条件,单值有限连续。 夕四、薛定语方程
第 22 章 量子力学基础 一、德布罗意物质波 德布罗意认为不仅光具有波粒二象性,实物粒子也具有波粒二象性。描述实物粒子波函数中 的 、 与实物粒子的能量 E 和动量 p 的德布罗意关系: 戴维孙-革末电子衍射实验,约恩孙电子双缝干涉实验都证实了电子具有的波动性。 二、海森伯不确定关系 由于微观粒子具有波粒二象性,我们就无法同时精确地测定微观粒子坐标与动量,海森伯提 出了如下的不确定关系: 1、动量-坐标不确定关系 2、时间-能量不确定关系 三、波函数 微观粒子具有波粒二象性,它不同于经典的波也不同于经典的粒子,要描述微观粒子群体随 时间的变化,引入波函数。波函数确定后,微观粒子的波粒二象性就能得到准确的描述。波 函数是微观粒子的态函数。 1、波函数的物理意义: 某一时刻在空间某一位置粒子出现的几率正比于该时刻该位置波函数的平方,或 ,即 几率密度 2、波函数的归一化条件 3、波函数的标准条件,单值有限连续。 四、薛定谔方程

薛定谔方程是量子力学的基础方程,由它可解出粒子的波函数 1、自由粒子: =2m a=e 22 2m V 2、势场中粒子: *非定态: 式中 ,为哈密顿算符。 定态:Aw)=Ew 夕五、薛定得方程应用实例 1、一维势箱:金属中电子、原子核中质子势能分布的理想化模型。它的势函数 00<x<(阱内) ()=。x≤0减x2L(阱外) 阱内一维定态薛定谔方程 h2dw =Ew 2d次2 x 解得满足边界条件(标准条件)归一化条件的解的波函数 v国是受 能量
薛定谔方程是量子力学的基础方程,由它可解出粒子的波函数 1、自由粒子: , , 2、势场中粒子: *非定态: 式中 ,为哈密顿算符。 定态: 五、薛定谔方程应用实例 1、一维势箱:金属中电子、原子核中质子势能分布的理想化模型。它的势函数 阱内一维定态薛定谔方程 解得满足边界条件(标准条件)归一化条件的解的波函数 能量
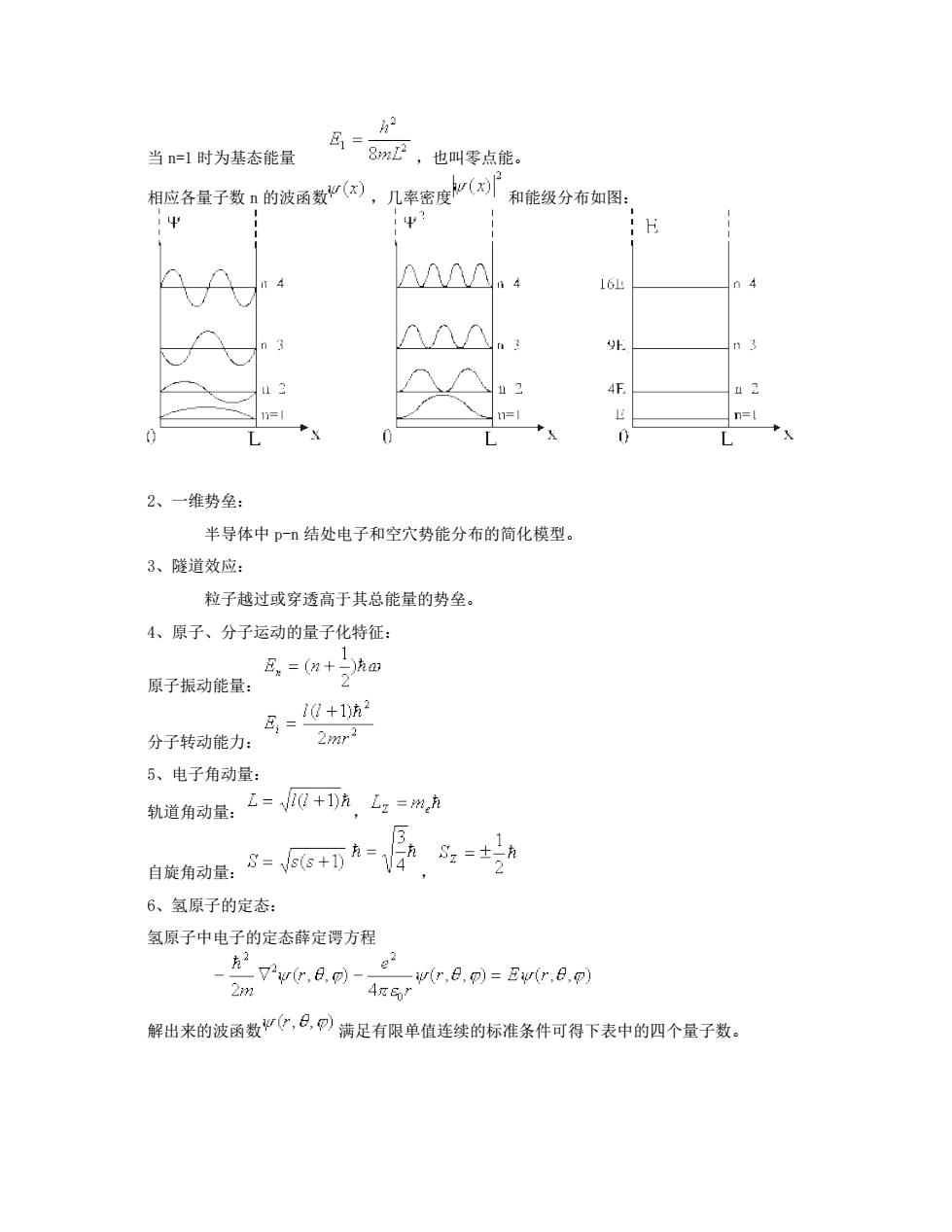
当n=l时为基态能量 区=8正,也叫零点能· 相应各量子数口的波函数因,几率密度加(和能级分布如图: 1Ψ AAAA 16 2、一维势垒: 半导体中pn结处电子和空穴势能分布的简化模型。 3、隧道效应: 粒子越过或穿透高于其总能量的势垒。 4、原子、分子运动的量子化特征: 原子振动能量: ,=0+2hm 鸟=0+1产 分子转动能力: 2mr2 5、电子角动量: 轨道角动量:=+,2=,方 自能角动量,8=58+D有=方品,=±力 6、氢原子的定态 氢原子中电子的定态薛定调方程 7v.8可4 r(r,日,p)=Ewr,8, 2m 解出来的波函数,日,满足有限单值连续的标准条件可得下表中的四个量子数
当 n=1 时为基态能量 ,也叫零点能。 相应各量子数 n 的波函数 ,几率密度 和能级分布如图: 2、一维势垒: 半导体中 p-n 结处电子和空穴势能分布的简化模型。 3、隧道效应: 粒子越过或穿透高于其总能量的势垒。 4、原子、分子运动的量子化特征: 原子振动能量: 分子转动能力: 5、电子角动量: 轨道角动量: , 自旋角动量: , 6、氢原子的定态: 氢原子中电子的定态薛定谔方程 解出来的波函数 满足有限单值连续的标准条件可得下表中的四个量子数
9 四个量子数表征氢原子中电子状态的特征,如表所列: 名称 可取数值 住要作用 主量子数n 正整数 确定电子能量的主要部分 1,2,3… =8 角量子数 在n给定以后,{可取n个确定电子的角动量 值,即0,1,2…(-1) L=2+1 相应常用s、D、d、f表示 磁量子数州 在!给定以后,可取2+1或确定角动量在外磁场方向的投影 2+1个值,即0,士1, L:=mgh ±2 自旋量子数, 只取两个值, 的定电子的自旋角对银5, 2沿 区恤能 原子中不可能有两个或两个以上的电子具有完全相同的量子态,或者说一个原子中任何两个 电子不可能具完全相同的四个量子数。 3、能量最小原理 原子系统中每个电子趋向占有最低能级,当原子系统的总能量为最小时原子最稳定。 夕大、多电子限 1、四个量子数 ,1,%, 2、泡利不相容原理 号七、经典粒子和徽观粒子描述比较 经典粒子 微观粒子 状态描述 r()p) w《,),一组量子数 运动图象 确定的动量、位置和轨迹 确定的几率分布
四个量子数表征氢原子中电子状态的特征,如表所列: 名称 可取数值 主要作用 主量子数 n 正整数 1,2,3…… 确定电子能量的主要部分 角量子数 在 n 给定以后, 可取 n 个 值,即 0,1,2……(n-1) 相应常用 s、p、d、f 表示 确定电子的角动量 磁量子数 在 给定以后,可取 或 个值,即 0, , …… 确定角动量在外磁场方向的投影 自旋量子数 只取两个值, 确定电子的自旋角动量 沿 某一方向上的投影 原子中不可能有两个或两个以上的电子具有完全相同的量子态,或者说一个原子中任何两个 电子不可能具完全相同的四个量子数。 3、能量最小原理 原子系统中每个电子趋向占有最低能级,当原子系统的总能量为最小时原子最稳定。 六、多电子原子 1、四个量子数 2、泡利不相容原理 七、经典粒子和微观粒子描述比较 经典粒子 微观粒子 状态描述 , ,一组量子数 运动图象 确定的动量、位置和轨迹 确定的几率分布

基础规律 F=dm可 薛定谔方程 牛顿定律 粒子状态 取决于力函数P,) 取决于势能函数(,) 力学量特征 连续变化 本征量量子化,非本征量不确 号固休量子理论基础 一、品体 分子、原子按一定的周期性作规则排列的固体称为品体。 1、按结合键分:离子晶体、共价品体、分子晶体、金属晶体、氢键晶体。 2、按导电性分:导体、半导体、绝缘体。 二、电子波函数 1、周期性势场:(x+=x) 久、布洛赫波函数:w(四=e业4(),6+)= 三、电子的能态 1、能带:N个相近能级组成,对应原子能级。 2、禁带:能带之间的禁区,电子不可能具有禁区能量。 四、电子运动 人速度, 2、加速度: m=2马1 3、有效质量: 3 五、半导体 1、本征导电性 2、杂质导电性:n型半导体、p型半导体 六、超导BCS理论
基础规律 牛顿定律 薛定谔方程 粒子状态 取决于力函数 取决于势能函数 力学量特征 连续变化 本征量量子化,非本征量不确 定 固体量子理论基础 一、晶体 分子、原子按一定的周期性作规则排列的固体称为晶体。 1、按结合键分:离子晶体、共价晶体、分子晶体、金属晶体、氢键晶体。 2、按导电性分:导体、半导体、绝缘体。 二、电子波函数 1、周期性势场: 2、布洛赫波函数: , 三、电子的能态 1、能带:N 个相近能级组成,对应原子能级。 2、禁带:能带之间的禁区,电子不可能具有禁区能量。 四、电子运动 1、速度: 2、加速度: 3、有效质量: 五、半导体 1、本征导电性。 2、杂质导电性:n 型半导体、p 型半导体。 六、超导 BCS 理论