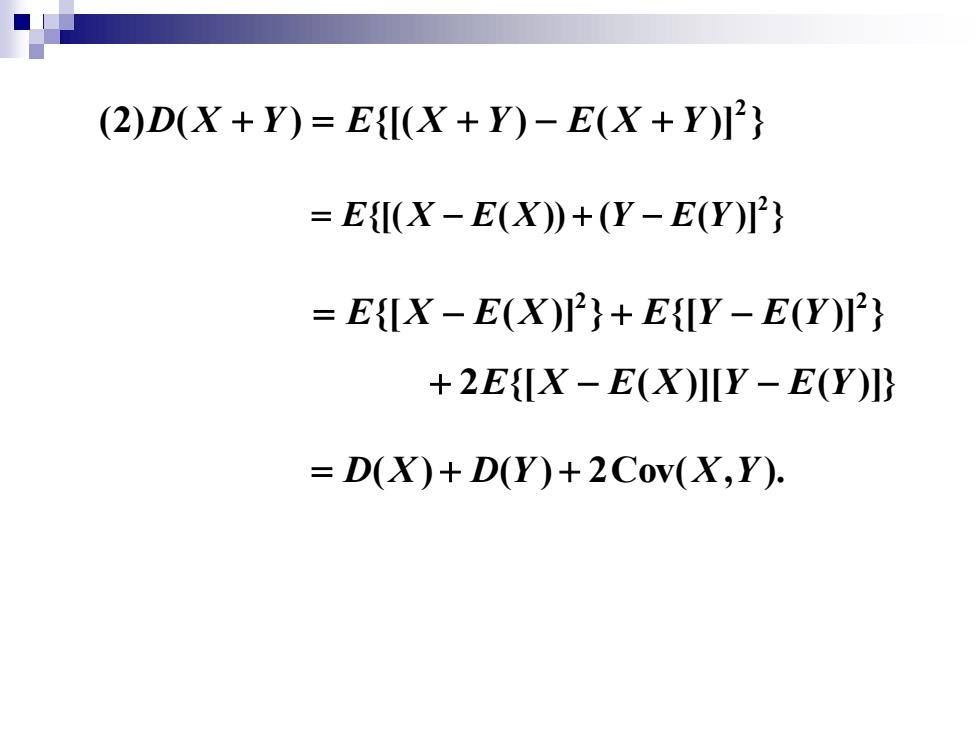
(2)D(X+Y)=E[(X+Y)-E(X+Y)J2} =E{I(X-E(X)+(Y-E(Y)I2)} =EX-E(X)+EY-E(Y) +2EX-E(XJY-E(Y)I =D(X)+D(Y)+2Cov(X,Y)
(2) ( ) {[( ) ( )] } 2 D X + Y = E X + Y − E X + Y {[( ( )) ( ( )] } 2 = E X − E X + Y − E Y + 2E{[X − E(X)][Y − E(Y )]} {[ ( )] } {[ ( )] } 2 2 = E X − E X + E Y − E Y = D(X) + D(Y ) + 2Cov(X,Y )

5.性质 (1)Cov(X,Y)=Cov(Y,X); (2)Cov(aX,bY)=abCov(X,Y),a,b为常数; (3)Cov(X+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
5. 性质 (1) Cov(X,Y ) = Cov(Y, X); (2) Cov(aX,bY) = abCov(X,Y), a, b为常数; (3) Cov( , ) Cov( , ) Cov( , ). X1 + X2 Y = X1 Y + X2 Y

例1设(X,Y)~N(4,42,o,o,p试求X与Y的 相关系数 解由f(x,y)= 1 2πo1o2V1-p nn-pa,门 _(x-41)2 →fx(x)=厅 e 「√2元0 2m,-0<x<+o0, _(y-2)2 f(y)=2π02 2o ,-0<y<+o0
. ( , ) ~ ( , , , , ), 22 2 1 2 1 相关系数设 X Y N μ μ σ σ ρ 试求 X 与Y 的 解 − + − − − − −− − = 22 2 2 1 2 1 2 21 2 1 2 2 1 2 ( )( ) ( ) 2 ( ) 2(1 ) 1 exp 2π 1 1 ( , ) σ y μ σ σ x μ y μ ρ σ x μ ρ σ σ ρ 由 f x y e , , 2π1 ( ) 21 2 1 2 ( ) 1 = − + − − x σ f x σ x μ X e , . 2π1 ( ) 22 2 2 2 ( ) 2 = − + − − y σ f y σ y μ Y 例 1

→E(X)=41,E(Y)=42,D(X)=o1,D(Y)=o. 而 Cov(X.Y)-(x-mX(y-/)f(x.y)dxdy 1 2nc0:1-(y-) dvdx了 。2o1.2(1-p2)L2 令t= n2- 01
( ) , ( ) , ( ) , ( ) . 2 2 2 E X = μ1 E Y = μ2 D X = σ1 D Y = σ Cov(X,Y ) (x μ )( y μ )f (x, y)d xd y 1 2 + − + − = − − 而 e e d d . ( )( ) 2π 1 1 2 1 1 2 2 2 2 1 2 1 2(1 ) 1 2 ( ) 2 1 2 1 2 y x x μ y μ σ σ ρ σ x μ ρ σ y μ σ ρ x μ − − − − − − − + − + − − − − = , 1 1 1 1 2 2 2 − − − − = σ x μ ρ σ y μ ρ 令 t , 1 1 σ x μ u − =