
非线性物理:孤波物理 反射势存在时: ·b化,O非零时GLM方程求解就很困难了,解析方法很少,多数用 数值方法和渐近分析方法。这里只是举例说明一些过程。 (I)u(化,0)=-u6y),u>0是常数,8x)是狄拉克函数。 对应u化,0)的薛定谔方程有分立本征值=-k(ku,/2),对应孤波 ;还有>0的连续谱,b(k,0)=u/u。+2i,对应色散波。 最后的解包含两部分:沿x方向传播的孤波和沿-x方向传播的色散 波。孤波对应B在+y,)的求和项,色散波对应于积分项
非线性物理:孤波物理 反射势存在时: • b(k, 0)非零时GLM方程求解就很困难了,解析方法很少,多数用 数值方法和渐近分析方法。这里只是举例说明一些过程。 • (1) u(x, 0)=-u0(x),u0>0是常数, (x) 是狄拉克函数。 • 对应u(x, 0)的薛定谔方程有分立本征值=-k12 (k1=u0/2),对应孤波 ;还有>0的连续谱,b(k, 0)=-u0/(u0+2ik),对应色散波。 • 最后的解包含两部分:沿x方向传播的孤波和沿-x方向传播的色散 波。孤波对应 B(x+y,t) 的求和项,色散波对应于积分项
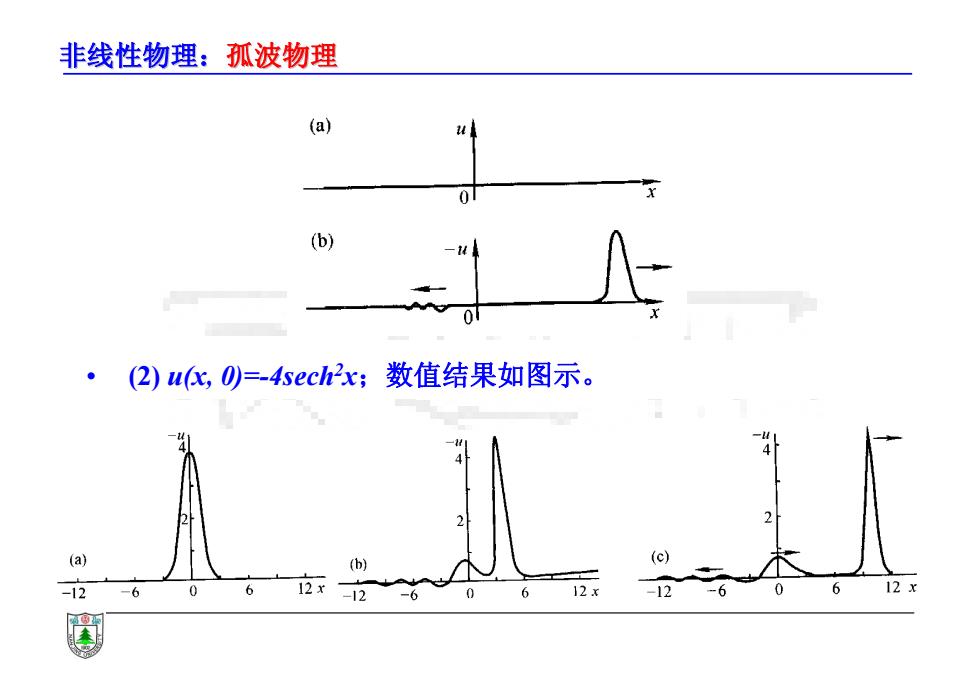
非线性物理:孤波物理 (a) 0 (b) ·(2)u,0)=-4echx;数值结果如图示。 a (b) (c) -12 -6 12x -12 12x -12 6 12X
非线性物理:孤波物理 • (2) u(x, 0)=-4sech2x;数值结果如图示
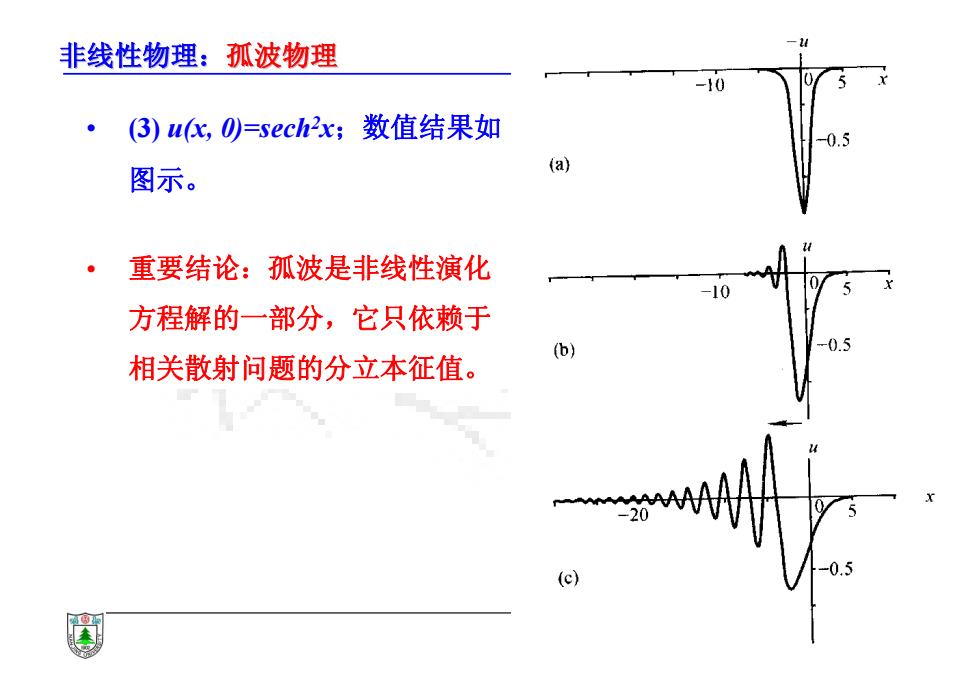
非线性物理:孤波物理 (3)u(:,O=sech2x;数值结果如 图示。 (a) 重要结论:孤波是非线性演化 方程解的一部分,它只依赖于 (b) 相关散射问题的分立本征值。 c
非线性物理:孤波物理 • (3) u(x, 0)=sech2x;数值结果如 图示。 • 重要结论:孤波是非线性演化 方程解的一部分,它只依赖于 相关散射问题的分立本征值

非线性物理:孤波物理 逆散射方法推广: ·Lax方法:1968年Lax将GGKM方法加以推广和标准化,称为Lax 方法。 Zakharovi和Shabat的推广矩阵方法。 AKNS独立的推广矩阵方法。 下面还要介绍一些方法,包括Backlund2变换,Backlund变换与逆 散射方法的关系
非线性物理:孤波物理 逆散射方法推广: • Lax方法:1968年Lax将GGKM方法加以推广和标准化,称为Lax 方法。 • Zakharov和Shabat的推广矩阵方法。 • AKNS独立的推广矩阵方法。 • 下面还要介绍一些方法,包括Backlund变换,Backlund变换与逆 散射方法的关系

非线性物理:孤波物理 Backlund-变换: 考虑如下sine-Gordon方程: uen sinu 。 如果和v都是方程的解,则有下面联立的一阶微分方程组: Ou Ov u+v +2λsin ∂5 05 2 λ≠O,real const. Bu Ov 2 u-V sIn- an an 2 我们称其为sine-Gordon方程的B变换
非线性物理:孤波物理 Backlund变换: • 考虑如下sine-Gordon方程: • 如果u和v都是方程的解,则有下面联立的一阶微分方程组: • 我们称其为sine-Gordon方程的B变换