
非线性物理:混沌物理 形态多样性:以平方映射为例 。 最简单动力学系统可以表示为(4为控制参数): y=(4,x) xn=f(u,xn) 1838年,生物学家Verhulst在研究生物种群演化时提出平方映 射演化方程,也即logistic map: x1-x) 数学物理学家R.May于1971年发现了这一单参量方程竞然具有 不同寻常的行为。微分形式(与迭代方程稍有不同): dx =x(1-x) dt
非线性物理:混沌物理 形态多样性:以平方映射为例 • 最简单动力学系统可以表示为( 为控制参数): yf x (,) • 1838年,生物学家 Verhulst 在研究生物种群演化时提出平方映 射演化方程,也即logistic map: ( , ) n 1 n x f x (1 ) n 1 n n x x x • 数学物理学家 R. May 于1971年发现了这一单参量方程竟然具有 不同寻常的行为。 微分形式(与迭代方程稍有不同): x(1 x) dt dx
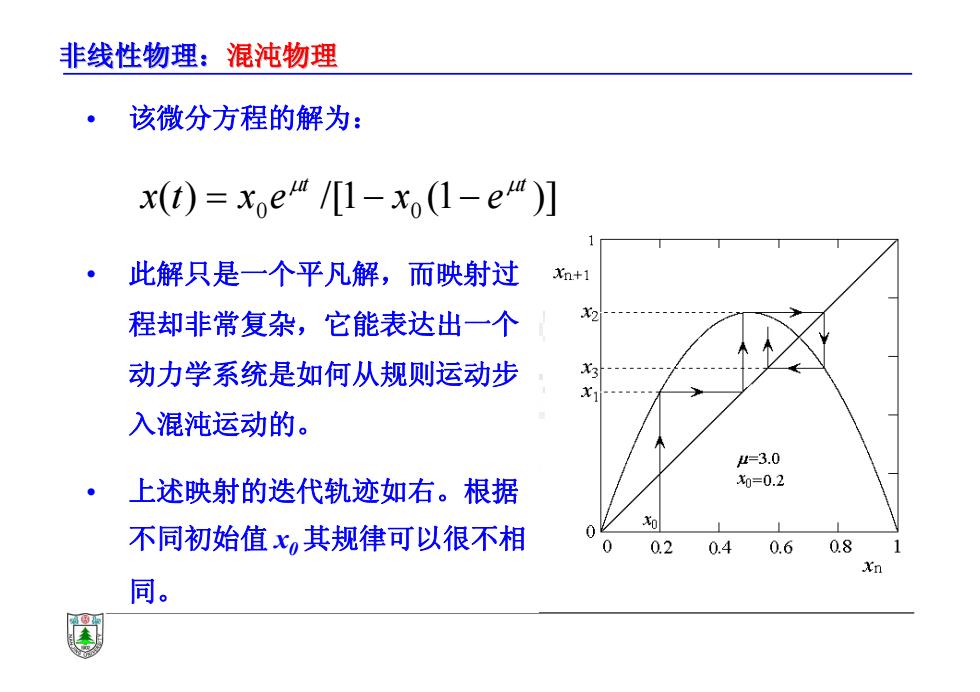
非线性物理:混沌物理 该微分方程的解为: x(t)=xe“/1-x(1-e“)] 此解只是一个平凡解,而映射过 Xn+1 程却非常复杂,它能表达出一个 动力学系统是如何从规则运动步 入混沌运动的。 4=3.0 ·上述映射的迭代轨迹如右。根据 x0=0.2 不同初始值x其规律可以很不相 0 0 0.20.4 0.608 Xn 同
非线性物理:混沌物理 • 该微分方程的解为: • 此解只是一个平凡解,而映射过 程却非常复杂,它能表达出一个 动力学系统是如何从规则运动步 入混沌运动的。 • 上述映射的迭代轨迹如右。根据 不同初始值 x0 其规律可以很不相 同。 ( ) /[1 (1 )] 0 0 t t x t x e x e
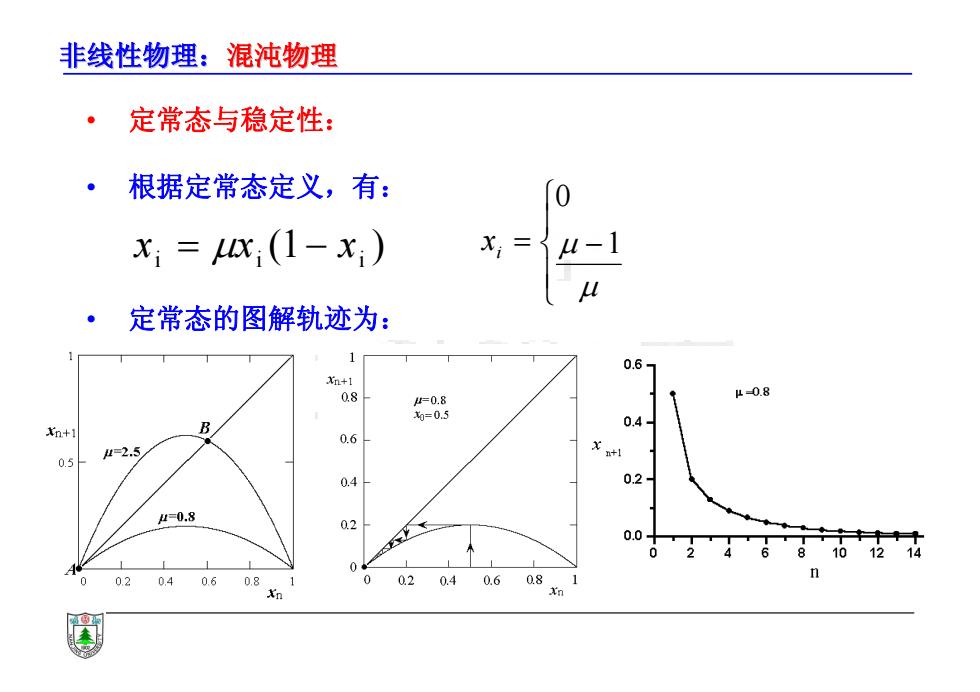
非线性物理:混沌物理 ·定常态与稳定性: 根据定常态定义,有: 0 x:=X(1-x) 定常态的图解轨迹为: 0.6 Xn+1 μ0.8 =0.8 0=0.5 Xn+ B 0.6 0.5 l-2.5 0.4 0.2 1=0.8 0.2 0.0 02 0406 0.8 0020.40.6081 n
非线性物理:混沌物理 • 定常态与稳定性: • 根据定常态定义,有: • 定常态的图解轨迹为: xxx iii ( ) 1 1 0 i x
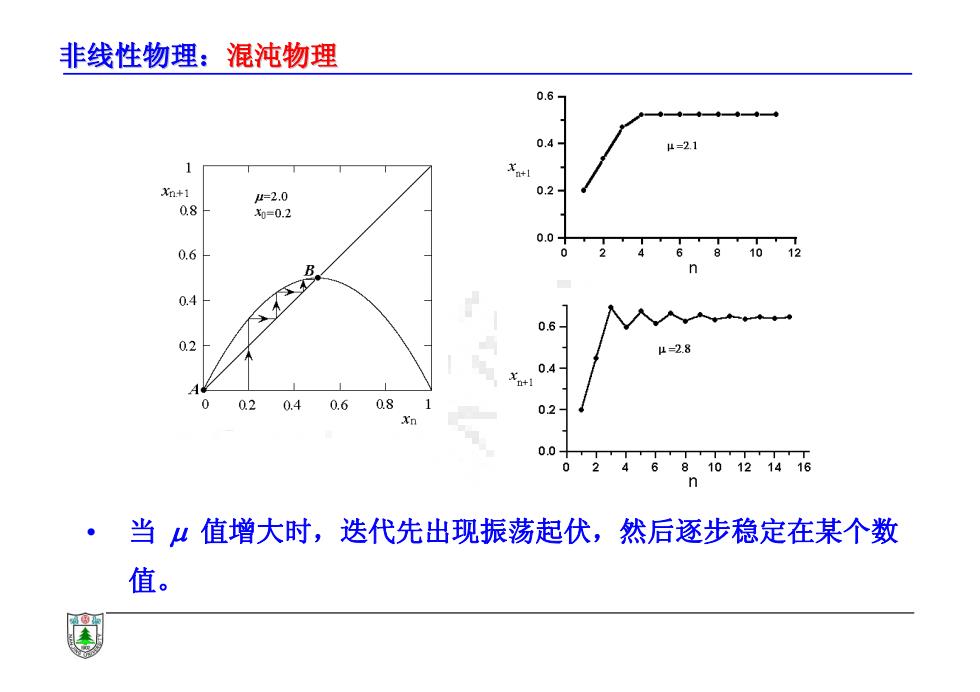
非线性物理:混沌物理 06 ◆◆◆◆◆◆ 0.4 μ=2.1 Xn+l Xn+1 1=2.0 0.2 08 0=0.2 0.0 0.6 0.4 0.6 0.2 1=2.8 0.4 A 0 0.20.4 0.60.8 02 Xn 0.0 0 46810121416 当山值增大时,迭代先出现振荡起伏,然后逐步稳定在某个数 值
非线性物理:混沌物理 • 当 值增大时,迭代先出现振荡起伏,然后逐步稳定在某个数 值

非线性物理:混沌物理 在定常态附近进行稳定性分析: x=f(uxn) x*=f(山,*) 在定常态x*处施加微扰6,则: x *+n=f(Lx*+n) x*+61=fu,x*)+4 8x x=x of(u,x) En 8x x=Y* 稳定不动点应该满足: Entl En m=≤1
非线性物理:混沌物理 • 在定常态附近进行稳定性分析: • 在定常态 x* 处施加微扰 n,则: ( , ) n 1 n x f x x* f (, x*) * ( , * ) n 1 n x f x n x x n x f x x f x * 1 ( , ) * ( , *) * 1 ( , ) n x x n x f x m • 稳定不动点应该满足: n+1 n m 1